Abstract
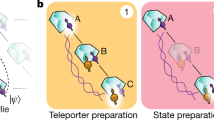
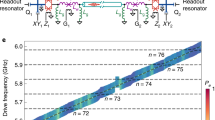
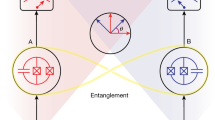
The generation of high-fidelity distributed multi-qubit entanglement is a challenging task for large-scale quantum communication and computational networks1,2,3,4. The deterministic entanglement of two remote qubits has recently been demonstrated with both photons5,6,7,8,9,10 and phonons11. However, the deterministic generation and transmission of multi-qubit entanglement has not been demonstrated, primarily owing to limited state-transfer fidelities. Here we report a quantum network comprising two superconducting quantum nodes connected by a one-metre-long superconducting coaxial cable, where each node includes three interconnected qubits. By directly connecting the cable to one qubit in each node, we transfer quantum states between the nodes with a process fidelity of 0.911 ± 0.008. We also prepare a three-qubit Greenberger–Horne–Zeilinger (GHZ) state12,13,14 in one node and deterministically transfer this state to the other node, with a transferred-state fidelity of 0.656 ± 0.014. We further use this system to deterministically generate a globally distributed two-node, six-qubit GHZ state with a state fidelity of 0.722 ± 0.021. The GHZ state fidelities are clearly above the threshold of 1/2 for genuine multipartite entanglement15, showing that this architecture can be used to coherently link together multiple superconducting quantum processors, providing a modular approach for building large-scale quantum computers16,17.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information 2nd edn (Cambridge Univ. Press, 2010).
Gottesman, D. & Chuang, I. L. Demonstrating the viability of universal quantum computation using teleportation and single-qubit operations. Nature 402, 390–393 (1999).
Duan, L.-M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Jiang, L., Taylor, J. M., Sørensen, A. S. & Lukin, M. D. Distributed quantum computation based on small quantum registers. Phys. Rev. A 76, 062323 (2007).
Kurpiers, P. et al. Deterministic quantum state transfer and remote entanglement using microwave photons. Nature 558, 264–267 (2018).
Axline, C. J. et al. On-demand quantum state transfer and entanglement between remote microwave cavity memories. Nat. Phys. 14, 705–710 (2018).
Campagne-Ibarcq, P. et al. Deterministic remote entanglement of superconducting circuits through microwave two-photon transitions. Phys. Rev. Lett. 120, 200501 (2018).
Leung, N. et al. Deterministic bidirectional communication and remote entanglement generation between superconducting qubits. npj Quantum Inf. 5, 18 (2019).
Zhong, Y. P. et al. Violating Bell’s inequality with remotely connected superconducting qubits. Nat. Phys. 15, 741–744 (2019).
Humphreys, P. C. et al. Deterministic delivery of remote entanglement on a quantum network. Nature 558, 268–273 (2018); publisher correction 562, E2 (2018).
Bienfait, A. et al. Phonon-mediated quantum state transfer and remote qubit entanglement. Science 364, 368–371 (2019).
Greenberger, D. M., Horne, M. A., Shimony, A. & Zeilinger, A. Bell’s theorem without inequalities. Am. J. Phys. 58, 1131–1143 (1990).
Neeley, M. et al. Generation of three-qubit entangled states using superconducting phase qubits. Nature 467, 570–573 (2010).
DiCarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010).
Gühne, O. & Seevinck, M. Separability criteria for genuine multiparticle entanglement. New J. Phys. 12, 053002 (2010).
Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).
Chou, K. S. et al. Deterministic teleportation of a quantum gate between two logical qubits. Nature 561, 368–373 (2018).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Rosenberg, D. et al. Solid-state qubits: 3D integration and packaging. IEEE Microw. Mag. 21, 72–85 (2020).
Magnard, P. et al. Microwave quantum link between superconducting circuits housed in spatially separated cryogenic systems. Phys. Rev. Lett. 125, 260502 (2020).
Bochmann, J., Vainsencher, A., Awschalom, D. D. & Cleland, A. N. Nanomechanical coupling between microwave and optical photons. Nat. Phys. 9, 712–716 (2013).
Mirhosseini, M., Sipahigil, A., Kalaee, M. & Painter, O. Superconducting qubit to optical photon transduction. Nature 588, 599–603 (2020).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Liao, S.-K. et al. Satellite-to-ground quantum key distribution. Nature 549, 43–47 (2017).
Chang, H.-S. et al. Remote entanglement via adiabatic passage using a tunably-dissipative quantum communication system. Phys. Rev. Lett. 124, 240502 (2020).
Burkhart, L. D. et al. Error-detected state transfer and entanglement in a superconducting quantum network. Preprint at https://arxiv.org/abs/2004.06168 (2020).
Chen, Y. et al. Qubit architecture with high coherence and fast tunable coupling. Phys. Rev. Lett. 113, 220502 (2014).
Wang, Y.-D. & Clerk, A. A. Using dark modes for high-fidelity optomechanical quantum state transfer. New J. Phys. 14, 105010 (2012).
Strauch, F. W. et al. Quantum logic gates for coupled superconducting phase qubits. Phys. Rev. Lett. 91, 167005 (2003).
Julsgaard, B., Kozhekin, A. & Polzik, E. S. Experimental long-lived entanglement of two macroscopic objects. Nature 413, 400–403 (2001).
Chou, C.-W. et al. Measurement-induced entanglement for excitation stored in remote atomic ensembles. Nature 438, 828–832 (2005).
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007).
Ritter, S. et al. An elementary quantum network of single atoms in optical cavities. Nature 484, 195–200 (2012).
Lee, K. C. et al. Entangling macroscopic diamonds at room temperature. Science 334, 1253–1256 (2011).
Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).
Roch, N. et al. Observation of measurement-induced entanglement and quantum trajectories of remote superconducting qubits. Phys. Rev. Lett. 112, 170501 (2014).
Narla, A. et al. Robust concurrent remote entanglement between two superconducting qubits. Phys. Rev. X 6, 031036 (2016).
Dickel, C. et al. Chip-to-chip entanglement of transmon qubits using engineered measurement fields. Phys. Rev. B 97, 064508 (2018).
Kurpiers, P. et al. Quantum communication with time-bin encoded microwave photons. Phys. Rev. Appl. 12, 044067 (2019).
Sillanpää, M. A., Park, J. I. & Simmonds, R. W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 449, 438–442 (2007).
Majer, J. et al. Coupling superconducting qubits via a cavity bus. Nature 449, 443–447 (2007).
Baksic, A., Ribeiro, H. & Clerk, A. A. Speeding up adiabatic quantum state transfer by using dressed states. Phys. Rev. Lett. 116, 230503 (2016).
Zhou, B. B. et al. Accelerated quantum control using superadiabatic dynamics in a solid-state lambda system. Nat. Phys. 13, 330–334 (2017).
Cirac, J. I., Zoller, P., Kimble, H. J. & Mabuchi, H. Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997).
Korotkov, A. N. Flying microwave qubits with nearly perfect transfer efficiency. Phys. Rev. B 84, 014510 (2011).
Sete, E. A., Mlinar, E. & Korotkov, A. N. Robust quantum state transfer using tunable couplers. Phys. Rev. B 91, 144509 (2015).
Yin, Y. et al. Catch and release of microwave photon states. Phys. Rev. Lett. 110, 107001 (2013).
Wenner, J. et al. Catching time-reversed microwave coherent state photons with 99.4% absorption efficiency. Phys. Rev. Lett. 112, 210501 (2014).
Srinivasan, S. J. et al. Time-reversal symmetrization of spontaneous emission for quantum state transfer. Phys. Rev. A 89, 033857 (2014).
Pechal, M. et al. Microwave-controlled generation of shaped single photons in circuit quantum electrodynamics. Phys. Rev. X 4, 041010 (2014).
Zeytinoğlu, S. et al. Microwave-induced amplitude-and phase-tunable qubit-resonator coupling in circuit quantum electrodynamics. Phys. Rev. A 91, 043846 (2015).
Xiang, Z. L., Zhang, M., Jiang, L. & Rabl, P. Intracity quantum communication via thermal microwave networks. Phys. Rev. X 7, 011035 (2017).
Vermersch, B., Guimond, P.-O., Pichler, H. & Zoller, P. Quantum state transfer via noisy photonic and phononic waveguides. Phys. Rev. Lett. 118, 133601 (2017).
Steffen, M. et al. Measurement of the entanglement of two superconducting qubits via state tomography. Science 313, 1423–1425 (2006).
Neeley, M. et al. Process tomography of quantum memory in a Josephson-phase qubit coupled to a two-level state. Nat. Phys. 4, 523–526 (2008).
Acknowledgements
We thank P. J. Duda, A. Clerk and K. J. Satzinger for discussions. We thank W. D. Oliver and G. Calusine at MIT Lincoln Lab for providing the travelling-wave parametric amplifier (TWPA) used in this work. Devices and experiments were supported by the Air Force Office of Scientific Research and the Army Research Laboratory. É.D. was supported by LDRD funds from Argonne National Laboratory; A.N.C. was supported in part by the DOE, Office of Basic Energy Sciences, and D.I.S. acknowledges support from the David and Lucile Packard Foundation. This work was partially supported by the University of Chicago’s MRSEC (NSF award DMR-2011854) and made use of the Pritzker Nanofabrication Facility, which receives support from SHyNE, a node of the National Science Foundation’s National Nanotechnology Coordinated Infrastructure (NSF grant number NNCI1542205), with additional support from NSF QLCI for HQAN (NSF award 2016136).
Author information
Authors and Affiliations
Contributions
Y.Z. designed and fabricated the devices, performed the measurement and analysed the data. H.-S.C. provided help with the measurement. A.B. and É.D. provided help with the infrastructure setup. A.N.C. and D.I.S. advised on all efforts. All authors contributed to discussions and production of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Damian Markham and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Figures S1–11 and Supplementary Tables S1–3.
Rights and permissions
About this article
Cite this article
Zhong, Y., Chang, HS., Bienfait, A. et al. Deterministic multi-qubit entanglement in a quantum network. Nature 590, 571–575 (2021). https://doi.org/10.1038/s41586-021-03288-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-021-03288-7
This article is cited by
-
On-demand directional microwave photon emission using waveguide quantum electrodynamics
Nature Physics (2023)
-
Quantum secure metrology for network sensing-based applications
Scientific Reports (2023)
-
Low-loss interconnects for modular superconducting quantum processors
Nature Electronics (2023)
-
Realizing all-to-all couplings among detachable quantum modules using a microwave quantum state router
npj Quantum Information (2023)
-
Photons go one way or another
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.