Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

High-throughput calculations of magnetic topological materials

Nature volume 586, pages 702–707 (2020)Cite this article

Subjects

Abstract

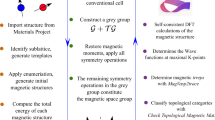
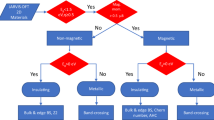
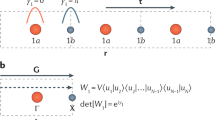
The discoveries of intrinsically magnetic topological materials, including semimetals with a large anomalous Hall effect and axion insulators1,2,3, have directed fundamental research in solid-state materials. Topological quantum chemistry4 has enabled the understanding of and the search for paramagnetic topological materials5,6. Using magnetic topological indices obtained from magnetic topological quantum chemistry (MTQC)7, here we perform a high-throughput search for magnetic topological materials based on first-principles calculations. We use as our starting point the Magnetic Materials Database on the Bilbao Crystallographic Server, which contains more than 549 magnetic compounds with magnetic structures deduced from neutron-scattering experiments, and identify 130 enforced semimetals (for which the band crossings are implied by symmetry eigenvalues), and topological insulators. For each compound, we perform complete electronic structure calculations, which include complete topological phase diagrams using different values of the Hubbard potential. Using a custom code to find the magnetic co-representations of all bands in all magnetic space groups, we generate data to be fed into the algorithm of MTQC to determine the topology of each magnetic material. Several of these materials display previously unknown topological phases, including symmetry-indicated magnetic semimetals, three-dimensional anomalous Hall insulators and higher-order magnetic semimetals. We analyse topological trends in the materials under varying interactions: 60 per cent of the 130 topological materials have topologies sensitive to interactions, and the others have stable topologies under varying interactions. We provide a materials database for future experimental studies and open-source code for diagnosing topologies of magnetic materials.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Band structures of the ‘high-quality’ magnetic topological materials predicted by MTQC.
Fig. 2: Topological surface states of representative magnetic topological insulator and enforced semimetal phases.

Data availability

All data are available in the Supplementary Information and at https://www.topologicalquantumchemistry.fr/magnetic. The codes required to calculate the character table of magnetic materials are available at https://www.cryst.ehu.es/cryst/checktopologicalmagmat.

References

  1. Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 9, 1–8 (2018).

    ADS  Google Scholar 

  2. Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).

    CAS  PubMed  PubMed Central  Google Scholar 

  3. Otrokov, M. M. et al. Prediction and observation of an antiferromagnetic topological insulator. Nature 576, 416–422 (2019).

    ADS  CAS  PubMed  Google Scholar 

  4. Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).

    ADS  CAS  PubMed  Google Scholar 

  5. Vergniory, M. G. et al. A complete catalogue of high-quality topological materials. Nature 566, 480–485 (2019).

    ADS  CAS  PubMed  Google Scholar 

  6. Zhang, T. et al. Catalogue of topological electronic materials. Nature 566, 475–479 (2019).

    ADS  CAS  PubMed  Google Scholar 

  7. Elcoro, L. et al. Magnetic topological quantum chemistry. Preprint at https://arxiv.org/abs/2010.00598 (2020).

  8. Kane, C. L. & Mele, E. J. Z 2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005).

    ADS  CAS  PubMed  Google Scholar 

  9. Bernevig, B. A. & Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).

    ADS  CAS  PubMed  Google Scholar 

  10. Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438–442 (2009).

    CAS  Google Scholar 

  11. Hsieh, T. H. et al. Topological crystalline insulators in the SnTe material class. Nat. Commun. 3, 982 (2012).

    ADS  PubMed  Google Scholar 

  12. Burkov, A. & Balents, L. Weyl semimetal in a topological insulator multilayer. Phys. Rev. Lett. 107, 127205 (2011).

    ADS  CAS  PubMed  Google Scholar 

  13. Wan, X., Ari, M. T., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).

    ADS  Google Scholar 

  14. Xu, G., Weng, H., Wang, Z., Dai, X. & Fang, Z. Chern semimetal and the quantized anomalous Hall effect in HgCr2Se4. Phys. Rev. Lett. 107, 186806 (2011).

    ADS  PubMed  Google Scholar 

  15. Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012).

    ADS  Google Scholar 

  16. Yang, B.-J. & Nagaosa, N. Classification of stable three-dimensional Dirac semimetals with nontrivial topology. Nat. Commun. 5, 4898 (2014).

    ADS  CAS  PubMed  Google Scholar 

  17. Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).

    Google Scholar 

  18. Huang, S.-M. et al. A Weyl fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).

    ADS  CAS  PubMed  PubMed Central  Google Scholar 

  19. Young, S. M. et al. Dirac semimetal in three dimensions. Phys. Rev. Lett. 108, 140405 (2012).

    ADS  CAS  PubMed  Google Scholar 

  20. Slager, R.-J., Mesaros, A., Juricic, V. & Zaanen, J. The space group classification of topological band-insulators. Nat. Phys. 9, 98–102 (2013).

    CAS  MATH  Google Scholar 

  21. Liu, C.-X., Zhang, R.-X. & VanLeeuwen, B. K. Topological nonsymmorphic crystalline insulators. Phys. Rev. B 90, 085304 (2014).

    ADS  Google Scholar 

  22. Wang, Z., Alexandradinata, A., Cava, R. J. & Bernevig, B. A. Hourglass fermions. Nature 532, 189–194 (2016).

    ADS  CAS  PubMed  Google Scholar 

  23. Wieder, B. J. et al. Wallpaper fermions and the nonsymmorphic Dirac insulator. Science 361, 246–251 (2018).

    ADS  CAS  PubMed  Google Scholar 

  24. Po, H. C., Vishwanath, A. & Watanabe, H. Symmetry-based indicators of band topology in the 230 space groups. Nat. Commun. 8, 50 (2017).

    ADS  PubMed  PubMed Central  Google Scholar 

  25. Kruthoff, J., de Boer, J., van Wezel, J., Kane, C. L. & Slager, R.-J. Topological classification of crystalline insulators through band structure combinatorics. Phys. Rev. X 7, 041069 (2017).

    Google Scholar 

  26. Song, Z., Zhang, T., Fang, Z. & Fang, C. Quantitative mappings between symmetry and topology in solids. Nat. Commun. 9, 3530 (2018).

    ADS  PubMed  PubMed Central  Google Scholar 

  27. Khalaf, E., Po, H. C., Vishwanath, A. & Watanabe, H. Symmetry indicators and anomalous surface states of topological crystalline insulators. Phys. Rev. X 8, 031070 (2018).

    CAS  Google Scholar 

  28. Tang, F., Po, H. C., Vishwanath, A. & Wan, X. Comprehensive search for topological materials using symmetry indicators. Nature 566, 486–489 (2019).

    ADS  CAS  PubMed  Google Scholar 

  29. Watanabe, H., Po, H. C. & Vishwanath, A. Structure and topology of band structures in the 1651 magnetic space groups. Sci. Adv. 4, eaat8685 (2018).

    ADS  CAS  PubMed  PubMed Central  Google Scholar 

  30. Hirschberger, M. et al. The chiral anomaly and thermopower of Weyl fermions in the half-Heusler GdPtBi. Nat. Mater. 15, 1161–1165 (2016).

    ADS  CAS  PubMed  Google Scholar 

  31. Yang, H. et al. Topological Weyl semimetals in the chiral antiferromagnetic materials Mn3Ge and Mn3Sn. New J. Phys. 19, 015008 (2017).

    ADS  Google Scholar 

  32. Li, H. et al. Dirac surface states in intrinsic magnetic topological insulators EuSn2As2 and MnBi2nTe3n+1. Phys. Rev. X 9, 041039 (2019).

    CAS  Google Scholar 

  33. Liu, D. F. et al. Magnetic Weyl semimetal phase in a kagomé crystal. Science 365, 1282–1285 (2019).

    ADS  CAS  PubMed  Google Scholar 

  34. Belopolski, I. et al. Discovery of topological Weyl fermion lines and drumhead surface states in a room temperature magnet. Science 365, 1278–1281 (2019).

    ADS  CAS  PubMed  Google Scholar 

  35. Zhang, D. et al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 122, 206401 (2019).

    ADS  CAS  PubMed  Google Scholar 

  36. Soh, J.-R. et al. Ideal Weyl semimetal induced by magnetic exchange. Phys. Rev. B 100, 201102 (2019).

    ADS  CAS  Google Scholar 

  37. Nie, S., Xu, G., Prinz, F. B. & Zhang, S.-C. Topological semimetal in honeycomb lattice LnSI. Proc. Natl Acad. Sci. USA 114, 10596–10600 (2017).

    ADS  CAS  PubMed  Google Scholar 

  38. Zou, J., He, Z. & Xu, G. The study of magnetic topological semimetals by first principles calculations. npj Comput. Mater. 5, 1–19 (2019).

    ADS  CAS  Google Scholar 

  39. Hua, G. et al. Dirac semimetal in type-IV magnetic space groups. Phys. Rev. B 98, 201116 (2018).

    ADS  Google Scholar 

  40. Shubnikov, A. V. Belov, N.V. & Holser, W.T. Colored Symmetry (Macmillan, 1964).

  41. Wieder, B. J. et al. Strong and fragile topological Dirac semimetals with higher-order Fermi arcs. Nat. Commun. 11, 627 (2020).

    ADS  CAS  PubMed  PubMed Central  Google Scholar 

  42. Xu, Y., Song, Z., Wang, Z., Weng, H. & Dai, X. Higher-order topology of the axion insulator EuIn2As2. Phys. Rev. Lett. 122, 256402 (2019).

    ADS  CAS  PubMed  Google Scholar 

  43. Wieder, B. J. & Bernevig, B. A. The axion insulator as a pump of fragile topology. Preprint at https://arxiv.org/abs/1810.02373 (2018).

  44. Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).

    ADS  Google Scholar 

  45. Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 58, 1799 (1987).

    ADS  CAS  PubMed  Google Scholar 

  46. Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).

    ADS  Google Scholar 

  47. Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).

    ADS  Google Scholar 

  48. Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).

    ADS  PubMed  Google Scholar 

  49. Hughes, T. L., Prodan, E. & Bernevig, B. A. Inversion-symmetric topological insulators. Phys. Rev. B 83, 245132 (2011).

    ADS  Google Scholar 

  50. Turner, A. M., Zhang, Y., Mong, R. S. K. & Vishwanath, A. Quantized response and topology of magnetic insulators with inversion symmetry. Phys. Rev. B 85, 165120 (2012).

    ADS  Google Scholar 

  51. Khalaf, E. Higher-order topological insulators and superconductors protected by inversion symmetry. Phys. Rev. B 97, 205136 (2018).

    ADS  Google Scholar 

  52. Li, C.-Z. et al. Reducing electronic transport dimension to topological hinge states by increasing geometry size of Dirac semimetal Josephson junctions. Phys. Rev. Lett. 124, 156601 (2020).

    ADS  CAS  PubMed  Google Scholar 

  53. Morali, N. et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 365, 1286–1291 (2019).

    ADS  CAS  PubMed  Google Scholar 

  54. Kuroda, K. et al. Evidence for magnetic Weyl fermions in a correlated metal. Nat. Mater. 16, 1090 (2017).

    ADS  CAS  PubMed  Google Scholar 

  55. Varnava, N., Souza, I. & Vanderbilt, D. Axion coupling in the hybrid Wannier representation. Phys. Rev. B 101, 155130 (2020).

    ADS  CAS  Google Scholar 

  56. Elcoro, L. et al. Double crystallographic groups and their representations on the Bilbao Crystallographic Server. J. Appl. Cryst. 50, 1457–1477 (2017).

    CAS  Google Scholar 

  57. Cano, J. et al. Building blocks of topological quantum chemistry: elementary band representations. Phys. Rev. B 97, 035139 (2018).

    ADS  CAS  Google Scholar 

  58. Vergniory, M. G. et al. Graph theory data for topological quantum chemistry. Phys. Rev. E 96, 023310 (2017).

    ADS  CAS  PubMed  Google Scholar 

  59. Song, Z., Huang, S.-J., Qi, Y., Fang, C. & Hermele, M. Topological states from topological crystals. Sci. Adv. 5, eaax2007 (2019).

    ADS  PubMed  PubMed Central  Google Scholar 

  60. Elcoro, L., Song, Z. & Bernevig, B. A. Application of induction procedure and smith decomposition in calculation and topological classification of electronic band structures in the 230 space groups. Phys. Rev. B 102, 035110 (2020).

    ADS  CAS  Google Scholar 

  61. Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61–66 (2017).

    ADS  MathSciNet  CAS  PubMed  MATH  Google Scholar 

  62. Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4, eaat0346 (2018).

    ADS  PubMed  PubMed Central  Google Scholar 

  63. Schindler, F. et al. Higher-order topology in bismuth. Nat. Phys. 14, 918–924 (2018).

    CAS  PubMed  PubMed Central  Google Scholar 

  64. Song, Z., Fang, Z. & Fang, C. (d − 2)-dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).

    ADS  PubMed  Google Scholar 

  65. Langbehn, J., Peng, Y., Trifunovic, L., von Oppen, F. & Brouwer, P. W. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 119, 246401 (2017).

    ADS  PubMed  Google Scholar 

  66. Po, H. C., Watanabe, H. & Vishwanath, A. Fragile topology and Wannier obstructions. Phys. Rev. Lett. 121, 126402 (2018).

    ADS  CAS  PubMed  Google Scholar 

  67. Cano, J. et al. Topology of disconnected elementary band representations. Phys. Rev. Lett. 120, 266401 (2018).

    ADS  CAS  PubMed  Google Scholar 

  68. Bradlyn, B., Wang, Z., Cano, J. & Bernevig, B. A. Disconnected elementary band representations, fragile topology, and Wilson loops as topological indices: an example on the triangular lattice. Phys. Rev. B 99, 045140 (2019).

    ADS  CAS  Google Scholar 

  69. Ahn, J., Park, S. & Yang, B.-J. Failure of Nielsen–Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle. Phys. Rev. X 9, 021013 (2019).

    CAS  Google Scholar 

  70. Song, Z.-D., Elcoro, L., Xu, Y.-F., Regnault, N. & Bernevig, B. A. Fragile phases as affine monoids: classification and material examples. Phys. Rev. X 10, 031001 (2020).

    CAS  Google Scholar 

  71. Gallego, S. V. et al. MAGNDATA: towards a database of magnetic structures. I. The commensurate case. J. Appl. Cryst. 49, 1750–1776 (2016).

    CAS  Google Scholar 

  72. Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).

    ADS  CAS  Google Scholar 

  73. Tran, F. & Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 102, 226401 (2009).

    ADS  PubMed  Google Scholar 

  74. Deng, X. Y., Wang, L., Dai, X. & Fang, Z. Local density approximation combined with Gutzwiller method for correlated electron systems: formalism and applications. Phys. Rev. B 79, 075114 (2009).

    ADS  Google Scholar 

  75. Wu, Q.S., Zhang, S. N., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: an open-source software package for novel topological materials. Comp. Phys. Commun. 224, 405–416 (2018).

  76. Gao, J., Wu, Q., Persson, C. & Wang, Z. Irvsp: to obtain irreducible representations of electronic states in the VASP. Preprint at https://arxiv.org/abs/2002.04032 (2020).

  77. Frey, N. C. et al. High-throughput search for magnetic and topological order in transition metal oxides. Preprint at https://arxiv.org/abs/2006.01075 (2020).

  78. Xu, Q. et al. Two-dimensional oxide topological insulator with iron-pnictide superconductor LiFeAs structure. Phys. Rev. B 92, 205310 (2015).

    ADS  Google Scholar 

  79. Wang, D. et al. Evidence for Majorana bound states in an iron-based superconductor. Science 362, 333–335 (2018).

    ADS  CAS  PubMed  Google Scholar 

Download references

Acknowledgements

We thank U. Schmidt, I. Weidl, W. Shi and Y. Zhang. We acknowledge the computational resources Cobra in the Max Planck Computing and Data Facility (MPCDF), the HPC Platform of ShanghaiTech University and Atlas in the Donostia International Physics Center (DIPC). Y.X. is grateful to D. Liu for help in plotting some diagrammatic sketches. B.A.B., N.R., B.J.W. and Z.S. were primarily supported by a Department of Energy grant (DE-SC0016239), and partially supported by the National Science Foundation (EAGER grant DMR 1643312), a Simons Investigator grant (404513), the Office of Naval Research (ONR; grant N00014-14-1-0330), the NSF-MRSEC (grant DMR-142051), the Packard Foundation, the Schmidt Fund for Innovative Research, the BSF Israel US foundation (grant 2018226), the ONR (grant N00014-20-1-2303) and a Guggenheim Fellowship (to B.A.B.). Additional support was provided by the Gordon and Betty Moore Foundation through grant GBMF8685 towards the Princeton theory programme. L.E. was supported by the Government of the Basque Country (Project IT1301-19) and the Spanish Ministry of Science and Innovation (PID2019-106644GB-I00). M.G.V. acknowledges support from the Diputacion Foral de Gipuzkoa (DFG; grant INCIEN2019-000356) from Gipuzkoako Foru Aldundia and the Spanish Ministerio de Ciencia e Innovación (grant PID2019-109905GB-C21). Y.C. was supported by the Shanghai Municipal Science and Technology Major Project (grant 2018SHZDZX02) and a Engineering and Physical Sciences Research Council (UK) Platform Grant (grant EP/M020517/1). C.F. acknowledges financial support by the DFG under Germany’s Excellence Strategy through the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter (ct.qmat EXC 2147, project-id 390858490), an ERC Advanced Grant (742068 ‘TOPMAT’). Y.X. and B.A.B. were also supported by the Max Planck Society.

Author information

Authors and Affiliations

  1. Max Planck Institute of Microstructure Physics, Halle, Germany

    Yuanfeng Xu & B. Andrei Bernevig

  2. Department of Condensed Matter Physics, University of the Basque Country UPV/EHU, Bilbao, Spain

    Luis Elcoro

  3. Department of Physics, Princeton University, Princeton, NJ, USA

    Zhi-Da Song, Benjamin J. Wieder, Nicolas Regnault & B. Andrei Bernevig

  4. Department of Physics, Massachusetts Institute of Technology, Cambridge, MA, USA

    Benjamin J. Wieder

  5. Department of Physics, Northeastern University, Boston, MA, USA

    Benjamin J. Wieder

  6. Donostia International Physics Center, Donostia/San Sebastian, Spain

    M. G. Vergniory

  7. IKERBASQUE, Basque Foundation for Science, Bilbao, Spain

    M. G. Vergniory

  8. Laboratoire de Physique de l’École normale supérieure, ENS, Université PSL, CNRS, Sorbonne Université, Université Paris-Diderot, Sorbonne Paris Cité, Paris, France

    Nicolas Regnault

  9. School of Physical Science and Technology, ShanghaiTech University, Shanghai, China

    Yulin Chen

  10. ShanghaiTech Laboratory for Topological Physics, Shanghai, China

    Yulin Chen

  11. Clarendon Laboratory, Department of Physics, University of Oxford, Oxford, UK

    Yulin Chen

  12. State Key Laboratory of Low Dimensional Quantum Physics, Department of Physics and Collaborative Innovation Center of Quantum Matter, Tsinghua University, Beijing, China

    Yulin Chen

  13. Max Planck Institute for Chemical Physics of Solids, Dresden, Germany

    Claudia Felser

  14. Center for Nanoscale Systems, Faculty of Arts and Science, Harvard University, Cambridge, MA, USA

    Claudia Felser

  15. Physics Department, Freie Universität Berlin, Berlin, Germany

    B. Andrei Bernevig

Authors
  1. Yuanfeng Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Luis Elcoro
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhi-Da Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Benjamin J. Wieder
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. M. G. Vergniory
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Nicolas Regnault
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Yulin Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Claudia Felser
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. B. Andrei Bernevig
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

B.A.B. conceived this work; Y.X. and M.G.V. performed the first-principles calculations. L.E. wrote the code for calculating the irreducible representations and checking the topologies of materials. Y.X., Z.S., B.J.W. and B.A.B. analysed the calculated results, B.J.W. determined the physical meaning of the topological indices with help from L.E., Z.S. and Y.X. C.F. performed chemical analysis of the magnetic topological materials. N.R. built the topological material database. All authors wrote the main text and Y.X. and Z.S. wrote the Methods and the Supplementary Information.

Corresponding author

Correspondence to B. Andrei Bernevig.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Peer review information Nature thanks the anonymous reviewers for their contribution to the peer review of this work.

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

This file contains Supplementary Sections 1–13, including 33 Supplementary Figures and 419 Supplementary Tables – see contents page for details.

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Xu, Y., Elcoro, L., Song, ZD. et al. High-throughput calculations of magnetic topological materials. Nature 586, 702–707 (2020). https://doi.org/10.1038/s41586-020-2837-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41586-020-2837-0

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing