Abstract
Loss of normal tissue architecture is a hallmark of oncogenic transformation1. In developing organisms, tissues architectures are sculpted by mechanical forces during morphogenesis2. However, the origins and consequences of tissue architecture during tumorigenesis remain elusive. In skin, premalignant basal cell carcinomas form ‘buds’, while invasive squamous cell carcinomas initiate as ‘folds’. Here, using computational modelling, genetic manipulations and biophysical measurements, we identify the biophysical underpinnings and biological consequences of these tumour architectures. Cell proliferation and actomyosin contractility dominate tissue architectures in monolayer, but not multilayer, epithelia. In stratified epidermis, meanwhile, softening and enhanced remodelling of the basement membrane promote tumour budding, while stiffening of the basement membrane promotes folding. Additional key forces stem from the stratification and differentiation of progenitor cells. Tumour-specific suprabasal stiffness gradients are generated as oncogenic lesions progress towards malignancy, which we computationally predict will alter extensile tensions on the tumour basement membrane. The pathophysiologic ramifications of this prediction are profound. Genetically decreasing the stiffness of basement membranes increases membrane tensions in silico and potentiates the progression of invasive squamous cell carcinomas in vivo. Our findings suggest that mechanical forces—exerted from above and below progenitors of multilayered epithelia—function to shape premalignant tumour architectures and influence tumour progression.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All RNA-sequencing data from this study have been deposited in the Gene Expression Omnibus (https://www.ncbi.nlm.nih.gov/geo/) under accession code GSE152488 (super-series). All other data in the manuscript, supplementary materials, source data and custom code are available from the corresponding author upon reasonable request. Source data are provided with this paper.
Code availability
Custom code for the multilayer vertex model is available upon request from M.K. (matej.krajnc@ijs.si), along with discussion/guidance for its use.
Change history
11 September 2020
A Correction to this paper has been published: https://doi.org/10.1038/s41586-020-2751-5
References
Hanahan, D. & Weinberg, R. A. Hallmarks of cancer: the next generation. Cell 144, 646–674 (2011).
Gilmour, D., Rembold, M. & Leptin, M. From morphogen to morphogenesis and back. Nature 541, 311–320 (2017).
Mohammadi, H. & Sahai, E. Mechanisms and impact of altered tumour mechanics. Nat. Cell Biol. 20, 766–774 (2018).
Pickup, M. W., Mouw, J. K. & Weaver, V. M. The extracellular matrix modulates the hallmarks of cancer. EMBO Rep. 15, 1243–1253 (2014).
Jones, P. H., Harper, S. & Watt, F. M. Stem cell patterning and fate in human epidermis. Cell 80, 83–93 (1995).
Atwood, S. X., Chang, A. L. & Oro, A. E. Hedgehog pathway inhibition and the race against tumor evolution. J. Cell Biol. 199, 193–197 (2012).
Crowson, A. N. Basal cell carcinoma: biology, morphology and clinical implications. Mod. Pathol. 19 (Suppl 2), S127–S147 (2006).
Li, S., Balmain, A. & Counter, C. M. A model for RAS mutation patterns in cancers: finding the sweet spot. Nat. Rev. Cancer 18, 767–777 (2018).
Beronja, S., Livshits, G., Williams, S. & Fuchs, E. Rapid functional dissection of genetic networks via tissue-specific transduction and RNAi in mouse embryos. Nat. Med. 16, 821–827 (2010).
Beronja, S. et al. RNAi screens in mice identify physiological regulators of oncogenic growth. Nature 501, 185–190 (2013).
Munjal, A. & Lecuit, T. Actomyosin networks and tissue morphogenesis. Development 141, 1789–1793 (2014).
Messal, H. A. et al. Tissue curvature and apicobasal mechanical tension imbalance instruct cancer morphogenesis. Nature 566, 126–130 (2019).
Farhadifar, R., Röper, J. C., Aigouy, B., Eaton, S. & Jülicher, F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr. Biol. 17, 2095–2104 (2007).
Daley, W. P. & Yamada, K. M. ECM-modulated cellular dynamics as a driving force for tissue morphogenesis. Curr. Opin. Genet. Dev. 23, 408–414 (2013).
Štorgel, N., Krajnc, M., Mrak, P., Štrus, J. & Ziherl, P. Quantitative morphology of epithelial folds. Biophys. J. 110, 269–277 (2016).
Pöschl, E. et al. Collagen IV is essential for basement membrane stability but dispensable for initiation of its assembly during early development. Development 131, 1619–1628 (2004).
Brown, K. L., Cummings, C. F., Vanacore, R. M. & Hudson, B. G. Building collagen IV smart scaffolds on the outside of cells. Protein Sci. 26, 2151–2161 (2017).
Fidler, A. L. et al. A unique covalent bond in basement membrane is a primordial innovation for tissue evolution. Proc. Natl Acad. Sci. USA 111, 331–336 (2014).
Yurchenco, P. D. Integrating activities of laminins that drive basement membrane assembly and function. Curr. Top. Membr. 76, 1–30 (2015).
Li, J. et al. Laminin-10 is crucial for hair morphogenesis. EMBO J. 22, 2400–2410 (2003).
DeRouen, M. C. et al. Laminin-511 and integrin beta-1 in hair follicle development and basal cell carcinoma formation. BMC Dev. Biol. 10, 112 (2010).
Asare, A., Levorse, J. & Fuchs, E. Coupling organelle inheritance with mitosis to balance growth and differentiation. Science 355, eaah4701 (2017).
Gonzales, K. A. U. & Fuchs, E. Skin and its regenerative powers: an alliance between stem cells and their niche. Dev. Cell 43, 387–401 (2017).
Büchau, F., Munz, C., Has, C., Lehmann, R. & Magin, T. M. KLHL16 degrades epidermal keratins. J. Invest. Dermatol. 138, 1871–1873 (2018).
Discher, D. E., Mooney, D. J. & Zandstra, P. W. Growth factors, matrices, and forces combine and control stem cells. Science 324, 1673–1677 (2009).
Chaudhuri, O. et al. Extracellular matrix stiffness and composition jointly regulate the induction of malignant phenotypes in mammary epithelium. Nat. Mater. 13, 970–978 (2014).
Crest, J., Diz-Muñoz, A., Chen, D. Y., Fletcher, D. A. & Bilder, D. Organ sculpting by patterned extracellular matrix stiffness. eLife 6, e24958 (2017).
Glentis, A. et al. Cancer-associated fibroblasts induce metalloprotease-independent cancer cell invasion of the basement membrane. Nat. Commun. 8, 924 (2017).
Harunaga, J. S., Doyle, A. D. & Yamada, K. M. Local and global dynamics of the basement membrane during branching morphogenesis require protease activity and actomyosin contractility. Dev. Biol. 394, 197–205 (2014).
Kelley, L. C. et al. Adaptive F-Actin polymerization and localized ATP production drive basement membrane invasion in the absence of MMPs. Dev. Cell 48, 313–328 (2019).
Mao, J. et al. A novel somatic mouse model to survey tumorigenic potential applied to the Hedgehog pathway. Cancer Res. 66, 10171–10178 (2006).
Chen, X. et al. Endogenous expression of HrasG12V induces developmental defects and neoplasms with copy number imbalances of the oncogene. Proc. Natl Acad. Sci. USA 106, 7979–7984 (2009).
Srinivas, S. et al. Cre reporter strains produced by targeted insertion of EYFP and ECFP into the ROSA26 locus. BMC Dev. Biol. 1, 4 (2001).
Muzumdar, M. D., Tasic, B., Miyamichi, K., Li, L. & Luo, L. A global double-fluorescent Cre reporter mouse. Genesis 45, 593–605 (2007).
Quiroz, F. G. et al. Liquid-liquid phase separation drives skin barrier formation. Science 367, eaax9554 (2020).
Luxenburg, C. et al. Wdr1-mediated cell shape dynamics and cortical tension are essential for epidermal planar cell polarity. Nat. Cell Biol. 17, 592–604 (2015).
Rauzi, M. & Lenne, P. F. Probing cell mechanics with subcellular laser dissection of actomyosin networks in the early developing Drosophila embryo. Methods Mol. Biol. 1189, 209–218 (2015).
Brown, A. C., Fiore, V. F., Sulchek, T. A. & Barker, T. H. Physical and chemical microenvironmental cues orthogonally control the degree and duration of fibrosis-associated epithelial-to-mesenchymal transitions. J. Pathol. 229, 25–35 (2013).
Costa, K. D., Sim, A. J. & Yin, F. C. Non-Hertzian approach to analyzing mechanical properties of endothelial cells probed by atomic force microscopy. J. Biomech. Eng. 128, 176–184 (2006).
Fiore, V. F. et al. αvβ3 Integrin drives fibroblast contraction and strain stiffening of soft provisional matrix during progressive fibrosis. JCI Insight 3, e97597 (2018).
Nowak, J. A. & Fuchs, E. Isolation and culture of epithelial stem cells. Methods Mol. Biol. 482, 215–232 (2009).
Ouspenskaia, T., Matos, I., Mertz, A. F., Fiore, V. F. & Fuchs, E. WNT-SHH antagonism specifies and expands stem cells prior to niche formation. Cell 164, 156–169 (2016).
Dobin, A. et al. STAR: ultrafast universal RNA-seq aligner. Bioinformatics 29, 15–21 (2013).
Love, M. I., Huber, W. & Anders, S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 15, 550 (2014).
Huang, W., Sherman, B. T. & Lempicki, R. A. Bioinformatics enrichment tools: paths toward the comprehensive functional analysis of large gene lists. Nucleic Acids Res. 37, 1–13 (2009).
Acknowledgements
We thank I. Matos, A. Asare, B. Hurwitz, S. Yuan, L. Polak, L. Hidalgo and M. Sribour for discussions and/or assistance; Y. Rominey in Memorial Sloan Kettering’s Molecular Cytology core for assistance with AFM; and Rockefeller University’s shared resources: the Bio-Imaging Center for microscope usage, and the Comparative Bioscience Center (AAALAC-accredited) for mouse care in accordance with NIH guidelines. V.F.F. was supported by the NIH–National Cancer Institute (NCI) Cancer Biology Training Program (grant CA009673-39) and a Charles H. Revson Senior Fellowship in Biomedical Sciences (Revson Foundation). M.K. was supported by the Slovenian Research Agency (research project Z1-1851). F.G.Q. holds a Career Award at the Scientific Interface from Burroughs Wellcome Fund. E.F. is a Howard Hughes Medical Institute (HHMI) Investigator. This research was supported by NIH grant R01-AR27883 to E.F.
Author information
Authors and Affiliations
Contributions
V.F.F. and E.F. conceived the experiments and wrote the manuscript, with contributions from M.K. and F.G.Q. M.K. and S.Y.S. developed the mathematical modelling. F.G.Q. designed and cloned transgenic constructs. J.L. performed lentiviral injections. H.A.P. performed ultrastructural analysis. V.F.F. performed all remaining experiments, data analyses and quantifications.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Salvador Benitah, Nicolas Minc and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Extended characterization of oncogenic tissue architecture models.
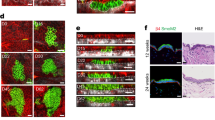
a, Characterization of adult SCCs. E9.5 oncogenic embryos were infected in utero with LV–Cre to selectively transduce single-layered embryonic epidermis. Tissues were harvested at three months (HRasG12V SCCs) and stained with haematoxylin and eosin (H & E). Epi, epithelium; Krt pearl, keratin pearl, a hallmark of SCCs; Str, stroma. Scale bars: left, 250 μm; right (zoom-in), 100 μm. b, Extended description of premalignant architectures and parameters used to quantify them. The schematics at the top show all parameters used here to quantify tissue and cell-shape parameters, including apical indentation depth (IA), basal indentation depth (IB), apical contour length (LA), basal contour length (LB), curvature radius (∅c), cell density (D) and cell aspect ratio (A). Bottom, quantification of S values (data repeated from Fig. 1d, 2i and contour length (LB/A; SmoM2, n = 11; HRasG12V, n = 11; mean + s.d.; Mann–Whitney U-test) for lesions from four embryos, two litters for each condition. We compare experimental measurements and simulation results (see Supplementary Note 1 for modelling details), which show strong agreement. However, we note that S is better able than LB/A to discriminate SmoM2 and HRasG12V phenotypes. c, Sagittal sections and whole-mount (planar) views show the distinct tissue shapes of SmoM2 and HRasG12V lesions. Measurements of IB and ∅c, from which S are calculated, are depicted on example images (sagittal view). d, Two-dimensional (2D) and 3D simulations of tissue shapes. Archetypal budded and folded tissue architectures were simulated in 3D and cut into 2D planes with varying cutting angles X and Z (see Supplementary Note 4 for details). The resultant tissues and their calculated S values are shown. Note that both architectures are equally well discerned without systematic bias (see the range of S values). Scale bars, 50 μm.
Extended Data Fig. 2 Cell proliferation drives skin tumour growth but not architectural differences between SmoM2 and HRasG12V lesions.
a, Cell proliferation as measured by EdU incorporation at E15.5. SmoM2- and HRasG12V-induced lesions are marked by YFP (left panels), and cell proliferation was quantified as the percentage of EdU+ basal cells in WT versus mutant lesions (centre panel; WT, n = 11; SmoM2, n = 11; HRasG12V, n = 12; one-way ANOVA with Tukey’s multiple comparisons test). The spatial distribution of WT cell proliferation in proximity to mutant clones was measured by quantifying the number EdU+ basal cells as a function of their neighbour distance from mutant clone edges (right panel; paired measurements from depicted tissue compartments; two-way ANOVA with Tukey’s multiple comparisons test). HF, hair follicle. b, Cell proliferation as measured by EdU incorporation at E18.5. SmoM2- and HRasG12V-induced lesions are marked by H2B–RFP. The graphs show cell proliferation, cell density (D) and aspect ratio (A; depicted in Extended Data Fig. 1b) at E18.5. Cell proliferation (WT, n = 8; SmoM2, n = 9; HRasG12V, n = 9; Kruskal–Wallis test with Dunn’s multiple comparisons test), D (WT, n = 9; SmoM2, n = 11; HRasG12V, n = 10; Kruskal–Wallis test with Dunn’s multiple comparisons test) and A (WT, n = 26; SmoM2, n = 22; HRasG12V, n = 36 cells; one-way ANOVA with Tukey’s multiple comparisons test) were measured for lesions from four embryos, two litters for each condition. c, Schematic showing our experimental approach to manipulating cell proliferation. LVs encoding H2B–GFP–iCRE and H2B–RFP–Cdkn1b under the control of a tetracycline-response element (TRE–Cdkn1b) were injected into SmoM2;K14–rtTA+ and HRasG12V;K14–rtTA+ mice. Embryos were injected with varying titres of TRE–Cdkn1b at E9.5, treated with doxycycline at E15.5, and harvested at E18.5. d, Cell-cycle manipulation was validated by measuring the EdU+ TRE–Cdkn1b+ (RFP+) and RFP− cells in both WT and oncogenic mutant backgrounds. e, Immunofluorescence and quantification of oncogenic tissue architectures in oncogenic mutant embryos infected with TRE–Cdkn1b. Quantification of lesion growth area (AG) and basal indentation depth (IB) shows that lesion size and deformations decrease with an increased titre of TRE–Cdkn1b similarly in SmoM2 (K14–rtTA–control, n = 11; 1:5 TRE–Cdkn1b, n = 11; 1:3 TRE–Cdkn1b, n = 10) and HRasG12V (K14–rtTA–control, n = 12; 1:5 TRE–Cdkn1b, n = 11; 1:3 TRE–Cdkn1b, n = 9) mutants from five embryos, two litters for each condition (one-way ANOVA with Tukey’s multiple comparisons test). All bar graphs show means + s.d. Scale bars, 50 μm. *P < 0.0001.
Extended Data Fig. 3 Role of interfacial actomyosin tension in a monolayer and multilayered epithelium.
a, Left, example time-lapse kymographs showing junctional laser ablation. Plasma membranes are marked by membrane-Tomato and membrane-GFP (mT and mG) in SmoM2;mTmG and HRasG12V;mTmG mice, with mutant cells (M) in green, wild-type (WT) cells in blue, and M–WT/WT–WT/M–M interfaces labelled. Laser cut sites are marked with pink dashed lines. Centre and right, the displacement of neighbouring tricellular junctions was quantified over time to yield retraction velocity curves. Initial retraction velocity values are shown for WT (n = 13), SmoM2, (M–WT, n = 9; M–M, n = 17; WT–WT, n = 8) and HRasG12V (M–WT, n = 10; M–M, n = 16; WT–WT, n = 17; one-way ANOVA with Tukey’s multiple comparisons test) from four to five embryos from two litters for each condition. b, Immunofluorescence staining of F-actin (using phalloidin) and phospho-S19-myosin-II (p-MyoII) in SmoM2 and HRasG12V lesions in sagittal sections (left) and planar whole-mount (right) views at E15.5. The intensity of staining is shown in heatmap values. p-MyoII polarization was measured in single basal cells (along the apicobasal axis, sagittal view; WT, n = 15; SmoM2, n = 18; HRasG12V, n = 16; one-way ANOVA with Tukey’s multiple comparisons test) and in whole clones (M–WT versus M–M interface, planar view; WT, n = 12; SmoM2, n = 12; HRasG12V, n = 16). Note that although p-MyoII is enriched basally, this polarization does not change between WT epidermal progenitors and oncogenic basal cells. c, Cell shapes analysed from E15.5 SmoM2 mutant clones. Cell area and anisotropy (defined as the ratio of major and minor cell axes) were analysed from whole-mount confocal images. Cells were automatically segmented on the basis of cortical E-cadherin staining. Note the increased anisotropy in M and WT cells at the clone border and the diminished cell area at the clone centre. d, The monolayer model epithelium. A single cell is transformed (green) and then undergoes cycles of division to induce tissue growth and deformation (see Supplementary Note 1). Interfacial tensions were varied in magnitude and orientation from basally to apically polarized, resulting in evaginating or invaginating lesions, respectively. e, Explant cultures treated with the actomyosin inhibitor Y-27632. SmoM2 oncogenic skin explants were treated with Y-27632 or vehicle control (DMSO) for 24 h before preparing the tissue for microscopic analysis (n = 11 lesions from three explants each; two-tailed unpaired t-test). All bar graphs show means + s.d. Scale bars, 50 μm. *P < 0.0001.
Extended Data Fig. 4 FACS sorting strategy and RNA-sequencing analysis of SmoM2 and HRasG12V tumours.
a, FACS strategy for isolating fluorescently marked basement membrane (BM)-associated (α6 integrinhi RFP+) basal progenitors from WT or oncogenic skins of E15.5 embryos. b, Principal component analysis (PCA) plots of n = 3 independent replicates of E15.5 oncogenic and WT basal progenitors reveals clustering of each replicate but distinct clustering across genetic lineages. c, Venn diagram showing genes upregulated or downregulated, comparing SmoM2 or HRasG12V mutants to WT basal progenitors. The overlap shows that 167 genes (6% of these differentially expressed genes) were coordinately upregulated in SmoM2 and downregulated in HRasG12V mutants.
Extended Data Fig. 5 Extended characterization of the mechanical properties of basement membrane.
a, Immunofluorescence images of the epidermal and dermal interfaces following EDTA-induced skin separation. Integrins (marked here by Itg-β4) on the progenitors’ basal surface delineate the underside of Krt14+ epidermis, while the basement membrane (marked here by LN-332) delineates the dermal surface of the tissue. To prepare samples for AFM measurements of basement-membrane stiffness, EBM, lentivirus-infected skin is harvested, and the epidermis is separated from dermis using EDTA treatment, leaving the basement membrane exposed on the dermal surface. HF, hair follicles. b, Example of AFM data analysis: a force-displacement curve for basement membrane, showing approach (red) and retraction (blue) curves, as well as the contact point (crosshairs). The equation for the Hertz model used to calculate EBM and its corresponding curve fit (black dotted line) is also shown. c, Stiffness, elasticity and plasticity of the basement membrane and dermis. The elasticity metric is defined as Elow/Ehigh, where a value of one represents absolute linear elasticity and values less than are increasingly nonlinear. The plasticity metric (L/L0) is defined as the difference in indentation lengths at zero force values between the approach and retraction curves. Measurements are from average force maps (basement membrane, n = 12; dermis, n = 14; two-tailed unpaired t-test) from four WT embryos. d, Stiffening of the basement membrane during epidermis and tumour development. AFM measurements are shown for WT basement membrane (left; E15.5, n = 10; E18.5, n = 12; Mann–Whitney U-test) and oncogenic lesions at E15.5 (right; SmoM2, n = 11; HRasG12V, n = 12; two-tailed unpaired t-test) and E18.5. The data for basement-membrane stiffness at E18.5 are the same as in c for purposes of comparison. e, Ultrastructural measurements. TEM images of the indicated regions show basement membrane (BM), dermis (Derm), epidermis (Epi) and hemidesmosomes (HD). Basement-membrane thickness is also quantified (SmoM2 (P), n = 14; SmoM2 (D), n = 12; HRasG12V, n = 14; one-way ANOVA with Tukey’s multiple comparisons). f, EBM measurements of shRNA-transduced and EDTA-treated skins (shScr, n = 9; shCol4a1, n = 9; shHspg2, n = 13; shPxdn, n = 13; Kruskal–Wallis test with Dunn’s multiple comparisons) from three embryos each. g, Representative immunofluorescence images of oncogenic skins from SmoM2 or HRasG12V embryos transduced with LV–Cre harbouring either Scr, Col4a1, Hspg2 or Pdxn shRNAs. S values are quantified (SmoM2: shScr, n = 13; shCol4a1, n = 10; shHspg2, n = 10; shPxdn, n = 10. HRasG12V: shScr, n = 13; shCol4a1, n = 11; shHspg2, n = 12; shPxdn, n = 11; Kruskal–Wallis test with Dunn’s multiple comparisons) from four embryos, two litters for each condition. All bar graphs show means + s.d. Scale bars, 50 μm. *P < 0.0001.
Extended Data Fig. 6 Extended characterization of the effects of basement-membrane assembly on tumour architectures.
a, Immunofluorescence of oncogenic skin sections. Note the enriched expression of nidogen (Nid1, a component of nascent basement membranes) at the leading edge of SmoM2 lesions, compared with the expression of LN-332 (a component of mature basement membranes), as shown by the ratiometric intensity heatmap. b, Our experimental approach for assaying the assembly rate of basement membranes, and experimental results. Oncogenic skin explants were harvested, and basement-membrane assembly rates were measured by exogenous pulse-labelling with fluorescent LN-β1 (Rd-LN), measuring its incorporation into native membranes over time. Example images are shown at the bottom left, with the intensity ratio of labelled LN-β1 and endogenous Nid1 immunostaining shown in heatmap. Bottom right, quantification of the LN-β1/Nid1 intensity ratio over time, with the slope (m) of each linear fit indicated. c, Changes in basement-membrane stiffness and assembly resulting from Lamb1 knockdown. Left, EBM measurements from shRNA-transduced WT embryos (shScr, n = 10; shLamb1, n = 12; independent regions from three embryos each; mean + s.d.; two-tailed unpaired t-test). Centre, assembly rates were measured as in b (shScr, n = 6; shLamb1, n = 6; Mann–Whitney U-test). Right, representative immunofluorescence images. d, Gain-of-function effects of LN-α5β1γ1 (LN-511) on tissue architecture. E16.5 oncogenic skin explants were cultured for 24 h with an excess (100 μg ml−1) of soluble LN-511 or vehicle control. Left, immunofluorescence staining for E-cadherin and RFP (SmoM2) or YFP and K14 (HRasG12V). Transduced cells are RFP+ and YFP+, respectively. Right, lesional S measurements for LN-511-treated oncogenic explants (SmoM2: control, n = 17; + LN-511, n = 10. HRasG12V: control, n = 9; + LN-511, n = 8; two-tailed unpaired t-test) from four embryos. All bar graphs show means + s.d. Scale bars, 50 μm.
Extended Data Fig. 7 Extended characterization of the effects of biophysical properties of the basement membrane on tumour architecture.
a, Left, a multilayer simulation was constructed to include WT cell proliferation in the absence or presence of the basement membrane. Simulated tissues with varying final numbers of WT cells (N) are shown. Right, basal indentation depth (IB) is quantified for varying values of basement-membrane stiffness (B) and assembly rate (1/τa). The extent of tissue deformations increases with increasing N, and this trend is globally conserved across multiple orders of magnitude and biophysical properties of basement membrane. b, The effect of interfacial tension on multilayer epithelia in the presence of basement membrane. Phase diagrams of S are shown are for γdiff = 0, 1.06 and 3.66. The effect is to gradually increase S values for an increasingly broad range of biophysical properties of the basement membrane. S, IB and cell density (D) phase diagrams from the multilayer model are shown for comparison with the monolayer simulations in c. c, The monolayer model, with mechanical properties of the basement membrane adjusted directly beneath transformed cells (see Supplementary Note 1). Shown (top) are phase diagrams for simulated tissue shapes predicted by the monolayer model as the stiffness and assembly rates of basement membrane are varied over the full parameter space, as well as (bottom) S, IB, and D simulations predicted by the monolayer model. d, Experimental measurements of cell density and proliferation in E18.5 WT, SmoM2 and HRasG12V skins and in oncogenic lesions transduced by shScr, shLamb1 or shCol4a1. Data are from four embryos, two litters for each condition (Kruskal–Wallis test with Dunn’s multiple comparisons). All bar graphs show means + s.d.
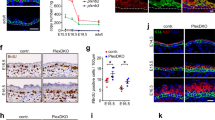
Extended Data Fig. 8 Measuring tissue mechanics, architecture and gene expression in human and adult mouse BCCs and SCCs.
a, AFM measurements of the stiffness of tumour compartments in human BCCs and SCCs. Left, immunofluorescence images of BCCs and SCCs, with force maps of the boxed areas shown below each image. Right, graph showing stiffness values for basal, keratin pearl (Krt Pearl) and suprabasal (SB) regions from BCCs (n = 6 regions from four tumours) and SCCs (n = 6 regions from three tumours). Paired measurements are compared between tumour type and tumour compartment (two-way ANOVA with Tukey’s multiple comparisons test). b, Curvature radius (∅c) values for human and mouse BCCs and SCCs (n = 5 tumours for each group; two-tailed unpaired t-test). c, Strategy for inducing SmoM2 in mice at postnatal day (P)21 and then harvesting 10 weeks later for FACS isolation and transcriptional profiling of α6hi YFP+ SmoM2+ basal progenitors from budded (Sca1−) and superficial (non-budded, Sca1+) tissue. d, GO terms for mRNAs upregulated in budded versus superficial BCC progenitors. Note that the ECM and basement-membrane categories are particularly enriched in budded progenitors. All bar graphs show means + s.d. Scale bars, 50 μm. *P < 0.0001.
Extended Data Fig. 9 Effects of a suprabasal stiffness gradient on tissue architectures.
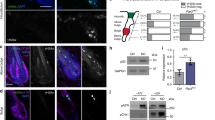
a, Right, phase diagrams of S and IA for the simulated tissue shapes shown at the left with the multilayer cell stiffness gradient for varying basement-membrane stiffness (B) and assembly rates (1/τa). For comparison, we show the same phase diagram for S as in Fig. 4b. b, Right, phase diagrams of S and IA for the simulated tissue shapes shown at the left without the multilayer cell stiffness gradient for varying B and 1/τa. For comparison, we show the same tissue shapes and phase diagram for S as in Fig. 2c, j, respectively. c, Manipulation of suprabasal cell stiffness with the ubiquitin ligase KLHL16. TRE–KLHL16–RFP was induced in suprabasal cells after treating Inv–rtTA mice with doxycycline at E9.5. d, Top, immunofluorescence staining shows a decrease in K10 intensity that overlaps with the RFP signal (arrow). Bottom left, AFM force maps from WT Inv–rtTA− and Inv–rtTA+ embryos at E18.5. Note the decreased stiffness that correlates with the RFP signal in Inv–rtTA+ embryos (arrow). Right, force maps were quantified and compared between RFP− and RFP+ regions of Inv–rtTA+ embryos and Inv–rtTA− embryos (mean + s.d., one-way ANOVA with Tukey’s multiple comparisons test). e, TRE–KLHL16–RFP was induced in suprabasal cells in the HRasG12V background using LV–Cre–H2B–GFP. Tissues harvested at E18.5 were analysed for IA, which correlated linearly with the extent of the TRE–KLHL16–RFP signal (r, Pearson’s correlation coefficient; n = 11 regions from four embryos). Scale bars, 50 μm.
Supplementary information
Supplementary Information
This file contains captions for Supplementary Videos 1-3, Supplementary Notes 1-4 and Supplementary References.
Supplementary Video 1
Computational simulation of a multilayer epithelium with differential junctional tensions. Shape evolution of the model multilayer tissue in the absence of the basement membrane at three values of differential tension (= 0, 0:163, and 1:057). All simulations start from a flat cross-sectional tissue and result in budded morphologies.
Supplementary Video 2
Computational simulation of a multilayer epithelium with basement membrane mechanics. Shape evolution of the model multilayer tissue attached to basement membrane. All simulations start from a flat cross-sectional tissue and result in budded, folded, and pearled morphologies [(B, τa) = (1:47876; 0:158489), (41:117; 0:158489), and (41:117; 398:107), respectively].
Supplementary Video 3
Computational simulation of a stratified epithelium with basement membrane and suprabasal cell mechanics. Shape evolution of the model multilayer tissue attached to the basement membrane in the presence of the suprabasal stiffness gradient. All simulations start from a flat cross-sectional tissue and result in budded, folded, and budded morphologies [(B, τa) = (1:47876; 0:158489), (41:117; 0:158489), and (41:117; 398:107), respectively].
Source data
Rights and permissions
About this article
Cite this article
Fiore, V.F., Krajnc, M., Quiroz, F.G. et al. Mechanics of a multilayer epithelium instruct tumour architecture and function. Nature 585, 433–439 (2020). https://doi.org/10.1038/s41586-020-2695-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2695-9
This article is cited by
-
Beyond genetics: driving cancer with the tumour microenvironment behind the wheel
Nature Reviews Cancer (2024)
-
Mechanical forces across compartments coordinate cell shape and fate transitions to generate tissue architecture
Nature Cell Biology (2024)
-
Profiling native pulmonary basement membrane stiffness using atomic force microscopy
Nature Protocols (2024)
-
Extracellular matrix remodeling in tumor progression and immune escape: from mechanisms to treatments
Molecular Cancer (2023)
-
Biophysics in tumor growth and progression: from single mechano-sensitive molecules to mechanomedicine
Oncogene (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.