Abstract
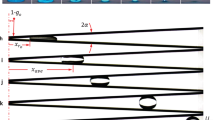
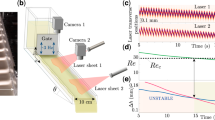
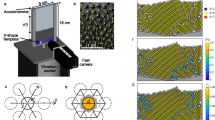
When placed over a less dense medium, a liquid layer will typically collapse downwards if it exceeds a certain size, as gravity acting on the lower liquid interface triggers a destabilizing effect called a Rayleigh–Taylor instability1,2. Of the many methods that have been developed to prevent the liquid from falling3,4,5,6, vertical shaking has proved to be efficient and has therefore been studied in detail7,8,9,10,11,12,13. Stabilization is the result of the dynamical averaging effect of the oscillating effective gravity. Vibrations of liquids also induce other paradoxical phenomena such as the sinking of air bubbles14,15,16,17,18,19 or the stabilization of heavy objects in columns of fluid at unexpected heights20. Here we take advantage of the excitation resonance of the supporting air layer to perform experiments with large levitating liquid layers of up to half a litre in volume and up to 20 centimetres in width. Moreover, we predict theoretically and show experimentally that vertical shaking also creates stable buoyancy positions on the lower interface of the liquid, which behave as though the gravitational force were inverted. Bodies can thus float upside down on the lower interface of levitating liquid layers. We use our model to predict the minimum excitation needed to withstand falling of such an inverted floater, which depends on its mass. Experimental observations confirm the possibility of selective falling of heavy bodies. Our findings invite us to rethink all interfacial phenomena in this exotic and counter-intuitive stable configuration.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
All the datasets generated during the current study are available in the Supplementary Information.
Change history
23 September 2020
A Correction to this paper has been published: https://doi.org/10.1038/s41586-020-2789-4
References
Lord Rayleigh. Investigation of the character of the equilibrium of an incompressible heavy fluid of variable density. Proc. Lond. Math. Soc. 14, 170–177 (1883).
Lewis, D. J. The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. II. Proc. R. Soc. Lond. A 202, 81–96 (1950).
Burgess, J. M., Juel, A., McCormick, W. D., Swift, J. B. & Swinney, H. L. Suppression of dripping from a ceiling. Phys. Rev. Lett. 86, 1203–1206 (2001).
Cimpeanu, R., Papageorgiou, D. T. & Petropoulos, P. G. On the control and suppression of the Rayleigh–Taylor instability using electric fields. Phys. Fluids 26, 022115 (2014).
Rannacher, D. & Engel, A. Suppressing the Rayleigh–Taylor instability with a rotating magnetic field. Phys. Rev. E 75, 016311 (2007).
Tao, J. J., He, X. T., Ye, W. H. & Busse, F. H. Nonlinear Rayleigh–Taylor instability of rotating inviscid fluids. Phys. Rev. E 87, 013001 (2013).
Wolf, G. H. The dynamic stabilization of the Rayleigh–Taylor instability and the corresponding dynamic equilibrium. Z. Phys. 227, 291–300 (1969).
Wolf, G. H. Dynamic stabilization of the interchange instability of a liquid–gas interface. Phys. Rev. Lett. 24, 444–446 (1970).
Lapuerta, V., Mancebo, F. J. & Vega, J. M. Control of Rayleigh–Taylor instability by vertical vibration in large aspect ratio containers. Phys. Rev. E 64, 016318 (2001).
Kumar, S. Mechanism for the Faraday instability in viscous liquids. Phys. Rev. E 62, 1416–1419 (2000).
Pototsky, A. & Bestehorn, M. Faraday instability of a two-layer liquid film with a free upper surface. Phys. Rev. Fluids 1, 023901 (2016).
Pototsky, A., Oron, A. & Bestehorn, M. Vibration-induced floatation of a heavy liquid drop on a lighter liquid film. Phys. Fluids 31, 087101 (2019).
Sterman-Cohen, E., Bestehorn, M. & Oron, A. Rayleigh–Taylor instability in thin liquid films subjected to harmonic vibration. Phys. Fluids 29, 052105 (2017); correction 29, 109901 (2017).
Baird, M. H. I. Resonant bubbles in a vertically vibrating liquid column. Can. J. Chem. Eng. 41, 52–55 (1963).
Jameson, G. J. The motion of a bubble in a vertically oscillating viscous liquid. Chem. Eng. Sci. 21, 35–48 (1966).
Sorokin, V. S., Blekhman, I. I. & Vasilkov, V. B. Motion of a gas bubble in fluid under vibration. Nonlinear Dyn. 67, 147–158 (2012).
Blekhman, I. I., Blekhman, L. I., Vaisberg, L. A., Vasil’kov, V. B. & Yakimova, K. S. “Anomalous” phenomena in fluid under the action of vibration. Dokl. Phys. 53, 520–524 (2008).
Blekhman, I. I., Blekhman, L. I., Sorokin, V. S., Vasilkov, V. B. & Yakimova, K. S. Surface and volumetric effects in a fluid subjected to high-frequency vibration. Proc. Inst. Mech. Eng. C 226, 2028–2043 (2012).
Zen’kovskaja, S. M. & Novosjadlyj, V. A. Vlijanie vertikal'nyh kolebanij na dvuhslojnuju sistemu s deformiruemoj poverhnost'ju razdela [Influence of vertical oscillations on a bilaminar system with a non-rigid interface.] Zh. Vychisl. Mat. Mat. Fiz. 48, 1710–1720 (2008).
Chelomei, V. N. Mechanical paradoxes caused by vibrations. Sov. Phys. Dokl. 28, 387–390 (1983).
Young, T. III. An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 95, 65–87 (1805).
Thomson, W. LX. On the equilibrium of vapour at a curved surface of liquid. Lond. Edinb. Dublin Philos. Mag. J. Sci. 42, 448–452 (1871).
de Gennes, P.-G., Brochard-Wyart, F. & Quere, D. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, Waves (Springer Science & Business Media, 2013).
Fermigier, M., Limat, L., Wesfreid, J. E., Boudinet, P. & Quilliet, C. Two-dimensional patterns in Rayleigh–Taylor instability of a thin layer. J. Fluid Mech. 236, 349–383 (1992).
Myshkis, A. D., Babskii, V. G., Kopachevskii, N. D., Slobozhanin, L. A. & Tyuptsov, A. Low-Gravity Fluid Mechanics. Mathematical Theory of Capillary Phenomena (Springer, 1987).
Faraday, M. On a peculiar class of acoustical figures; and on certain forms assumed by groups of particles upon vibrating elastic surfaces. Philos. Trans. R. Soc. Lond. 121, 299–340 (1831).
Douady, S. Experimental study of the Faraday instability. J. Fluid Mech. 221, 383–409 (1990).
Kumar, K. & Tuckerman, L. S. Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68 (1994).
Elbing, B. R., Still, A. L. & Ghajar, A. J. Review of bubble column reactors with vibration. Ind. Eng. Chem. Res. 55, 385–403 (2016).
Bjerknes, V. F. K. Fields of Force: Supplementary Lectures, Applications to Meteorology (Columbia Univ. Press and Macmillan, 1906).
Kapitza, P. L. Dynamic stability of a pendulum when its point of suspension vibrates. Sov. Phys. JETP 21, 588–597 (1951).
Krieger, M. S. Interfacial fluid instabilities and Kapitsa pendula. Eur. Phys. J. E 40, 67 (2017).
Landau, L. D. & Lifshitz, E. M. Mechanics (Pergamon, 1969).
Acknowledgements
We thank S. Protière, A. Lazarus, S. Wildeman and the staff and students of ‘Projets Scientifiques en Equipes’ for insightful discussions. We thank the AXA research fund and the French National Research Agency LABEX WIFI (ANR-10-LABX-24) for support.
Author information
Authors and Affiliations
Contributions
All the authors discussed, interpreted the results and conceived the theoretical framework. E.F. devised the initial idea. B.A. and F.N. designed and performed the experiments. B.A., F.N. and E.F. wrote the paper. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Koji Hasegawa, Vladislav Sorokin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Models and Supplementary Raw Data.
Video 1
Controlling the position of an air bubble in an oscillating bath The liquid is silicon oil shaken at a frequency of 100 Hz by changing the forcing amplitude A. The critical depth d* above which the bubble starts to sink decreases when the forcing amplitude is increased. Hence, the bubble can go up or down depending on the vibration. The frame is tuned to strobe the bath oscillation. The container has a horizontal section of 11×11 cm2.
Video 2
Making the liquid layer levitate. The air layer is obtained by blowing air at the bottom of the oscillating liquid bath through a needle. The sinking bubble grows up to completely fill the bottom of the bath. The liquid is silicon oil, the forcing frequency is 100 Hz. The forcing amplitude is initially 3 mm and is decreased after the creation of the levitating layer to avoid Faraday instability. The container has a horizontal section of 5×4 cm2.
Video 3
Faraday instability at the two interfaces of the levitating liquid layer. The liquid is silicon oil, the forcing frequency is 100 Hz. The forcing amplitude is tuned to start the Faraday instability. The container has a horizontal section of 5×4 cm2.
Video 4
Making two liquid layer levitate. The liquid is silicon oil, the forcing frequency is 100 Hz. The forcing amplitude is tuned during the process to control the size of the liquid layers. The container has a horizontal section of 5×4 cm2.
Video 5
Stabilization of a liquid layer. The liquid is silicon oil with a horizontal section of 18×2 cm2. The forcing frequency is 80 Hz.
Video 6
Boats floating at the interfaces of the levitating liquid layer. The liquid is silicon oil, the forcing frequency is 60 Hz. The container has a horizontal section of 14×2 cm2. The boat are made a light foam with a width of 1.5 cm and length of approximately 3 cm.
Video 7
Relative stability between a floater and the liquid layer. The liquid is silicon oil, the forcing frequency is 80 Hz. The container has a horizontal section of 5×4 cm2. The floater is a sphere with a diameter of 2.5 cm.
Rights and permissions
About this article
Cite this article
Apffel, B., Novkoski, F., Eddi, A. et al. Floating under a levitating liquid. Nature 585, 48–52 (2020). https://doi.org/10.1038/s41586-020-2643-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2643-8
This article is cited by
-
New physical insights in dynamical stabilization: introducing Periodically Oscillating-Diverging Systems (PODS)
Nonlinear Dynamics (2023)
-
Floating upside down
Nature Reviews Physics (2020)
-
Vibration overcomes gravity on a levitating fluid
Nature (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.