Abstract
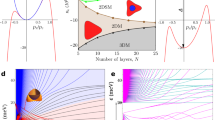
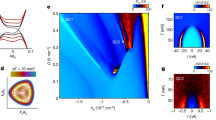
Of the two stable forms of graphite, hexagonal and rhombohedral, the former is more common and has been studied extensively. The latter is less stable, which has so far precluded its detailed investigation, despite many theoretical predictions about the abundance of exotic interaction-induced physics1,2,3,4,5,6. Advances in van der Waals heterostructure technology7 have now allowed us to make high-quality rhombohedral graphite films up to 50 graphene layers thick and study their transport properties. Here we show that the bulk electronic states in such rhombohedral graphite are gapped8 and, at low temperatures, electron transport is dominated by surface states. Because of their proposed topological nature, the surface states are of sufficiently high quality to observe the quantum Hall effect, whereby rhombohedral graphite exhibits phase transitions between a gapless semimetallic phase and a gapped quantum spin Hall phase with giant Berry curvature. We find that an energy gap can also be opened in the surface states by breaking their inversion symmetry by applying a perpendicular electric field. Moreover, in rhombohedral graphite thinner than four nanometres, a gap is present even without an external electric field. This spontaneous gap opening shows pronounced hysteresis and other signatures characteristic of electronic phase separation, which we attribute to emergence of strongly correlated electronic surface states.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Kopnin, N. B., Ijäs, M., Harju, A. & Heikkilä, T. T. High-temperature surface superconductivity in rhombohedral graphite. Phys. Rev. B 87, 140503(R) (2013).
Otani, M., Koshino, M., Takagi, Y. & Okada, S. Intrinsic magnetic moment on (0001) surfaces of rhombohedral graphite. Phys. Rev. B 81, 161403(R) (2010).
Zhang, F., Jung, J., Fiete, G. A., Niu, Q. & MacDonald, A. H. Spontaneous quantum Hall states in chirally stacked few-layer graphene systems. Phys. Rev. Lett. 106, 156801 (2011).
Pamuk, B., Baima, J., Mauri, F. & Calandra, M. Magnetic gap opening in rhombohedral-stacked multilayer graphene from first principles. Phys. Rev. B 95, 075422 (2017).
Muñoz, W. A., Covaci, L. & Peeters, F. M. Tight-binding description of intrinsic superconducting correlations in multilayer graphene. Phys. Rev. B 87, 134509 (2013).
Xu, D. H. et al. Stacking order, interaction, and weak surface magnetism in layered graphene sheets. Phys. Rev. B 86, 201404(R) (2012).
Yang, Y. et al. Stacking order in graphite films controlled by van der Waals technology. Nano Lett. 19, 8526–8532 (2019).
Ho, C. H., Chang, C. P. & Lin, M. F. Evolution and dimensional crossover from the bulk subbands in ABC-stacked graphene to a three-dimensional Dirac cone structure in rhombohedral graphite. Phys. Rev. B 93, 075437 (2016).
Haering, R. R. Band structure of rhombohedral graphite. Can. J. Phys. 36, 352–362 (1958).
Mcclure, J. W. Electron energy band structure and electronic properties of rhombohedral graphite. Carbon 7, 425–432 (1969).
Xiao, R. J. et al. Density functional investigation of rhombohedral stacks of graphene: topological surface states, nonlinear dielectric response, and bulk limit. Phys. Rev. B 84, 165404 (2011).
Xiao, D., Chang, M. C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959–2007 (2010).
Velasco, J. et al. Transport spectroscopy of symmetry-broken insulating states in bilayer graphene. Nat. Nanotechnol. 7, 156–160 (2012).
Lee, Y. et al. Competition between spontaneous symmetry breaking and single-particle gaps in trilayer graphene. Nat. Commun. 5, 5656 (2014).
Myhro, K. et al. Large tunable intrinsic gap in rhombohedral-stacked tetralayer graphene at half filling. 2D Mater. 5, 045013 (2018).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).
Lee, Y. et al. Gate tunable magnetism and giant magnetoresistance in ABC-stacked few-layer graphene. Preprint at http://arXiv.org/abs/1911.04450 (2019).
Henni, Y. et al. Rhombohedral multilayer graphene: a magneto-Raman scattering study. Nano Lett. 16, 3710–3716 (2016).
Henck, H. et al. Flat electronic bands in long sequences of rhombohedral-stacked graphene. Phys. Rev. B 97, 245421 (2018).
Shi, Y. et al. Tunable Lifshitz transitions and multiband transport in tetralayer graphene. Phys. Rev. Lett. 120, 096802 (2018).
Nakasuga, T. et al. Low-energy band structure in Bernal stacked six-layer graphene: Landau fan diagram and resistance ridge. Phys. Rev. B 99, 085404 (2019).
Koshino, M. Interlayer screening effect in graphene multilayers with ABA and ABC stacking. Phys. Rev. B 81, 125304 (2010).
Yin, J. et al. Dimensional reduction, quantum Hall effect and layer parity in graphite films. Nature Phys. 15, 437–442 (2019).
Koshino, M. & McCann, E. Trigonal warping and Berry’s phase Nπ in ABC-stacked multilayer graphene. Phys. Rev. B 80, 165409 (2009).
Min, H. K. & MacDonald, A. H. Chiral decomposition in the electronic structure of graphene multilayers. Phys. Rev. B 77, 155416 (2008).
Slizovskiy, S., McCann, E., Koshino, M. & Fal’ko, V. I. Films of rhombohedral graphite as two-dimensional topological semimetals. Commun. Phys. 2, 164 (2019).
Ran, S. et al. Phase diagram of URu2– xFexSi2 in high magnetic fields. Proc. Natl Acad. Sci. USA 114, 9826–9831 (2017).
Dagotto, E. Complexity in strongly correlated electronic systems. Science 309, 257–262 (2005).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Zhang, Y. et al. Crossover of the three-dimensional topological insulator Bi2Se3 to the two-dimensional limit. Nat. Phys. 6, 584–588 (2010); erratum 6, 712 (2010).
Neupane, M. et al. Observation of quantum-tunnelling-modulated spin texture in ultrathin topological insulator Bi2Se3 films. Nat. Commun. 5, 3841 (2014).
Cai, S. et al. Independence of topological surface state and bulk conductance in three-dimensional topological insulators. npj Quantum Mater. 3, 62 (2018).
Dresselhaus, M. S. & Dresselhaus, G. Intercalation compounds of graphite. Adv. Phys. 51, 1–186 (2002).
García-Ruiz, A., Slizovskiy, S., Mucha-Kruczynski, M. & Fal’ko, V. I. Spectroscopic signatures of electronic excitations in Raman scattering in thin films of rhombohedral graphite. Nano Lett. 19, 6152–6156 (2019).
Zhang, F. & MacDonald, A. H. Distinguishing spontaneous quantum Hall states in bilayer graphene. Phys. Rev. Lett. 108, 186804 (2012).
Lemonik, Y., Aleiner, I. & Fal’ko, V. I. Competing nematic, antiferromagnetic, and spin-flux orders in the ground state of bilayer graphene. Phys. Rev. B 85, 245451 (2012).
Kharitonov, M. Canted antiferromagnetic phase of the ν = 0 quantum Hall state in bilayer graphene. Phys. Rev. Lett. 109, 046803 (2012).
Kharitonov, M. Antiferromagnetic state in bilayer graphene. Phys. Rev. B 86, 195435 (2012).
Acknowledgements
This work was supported by the EU Graphene Flagship Program, the European Research Council, the Royal Society, and the Engineering and Physical Sciences Research Council (EPSRC). A.M. acknowledges the support of an EPSRC Early Career Fellowship (EP/N007131/1). S.V.M. was supported by the RFBR (20-02-00601). This work was partially supported by the French National Research Agency (ANR) in the framework of a RhomboG grant (ANR-17-CE24-0030).
Author information
Authors and Affiliations
Contributions
A.M. conceived the presented idea and directed the project. Y.S., S.V.M., S.O., C.M., J.B., J.Y., A.I.B. and B.A.P. performed transport measurements. S.X., Y.Y. and S.-K.S. fabricated devices. Y.S., S.O., C.M. and J.Y. performed data analysis. S.S. and V.I.F. developed the theory and performed theoretical calculations. Y.S., S.O., A.K.G., V.I.F. and A.M. contributed to the interpretation of data. K.W. and T.T. grew hBN single crystals. A.M., Y.S., A.K.G., S.S., V.I.F. and K.S.N. contributed to the writing of the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Dmitri Efetov and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Effect of stacking sequence on the displacement-field-induced bandgap.
a, b, Raman maps of device 3, a 6.5-nm graphite flake with domains of differing local stacking sequence, shown before (a) and after (b) encapsulation. The colour coding indicates the ratio of the integrated area of the low-frequency component of the graphite Raman 2D band (ranging around 2,670–2,700 cm−1) to that of the high-frequency component (ranging around 2,700–2,730 cm-1). Coloured dots in a and b mark the positions where the Raman spectra shown in c and d respectively were taken. Scale bars, 10 μm. c, d, Typical 2D Raman peaks of HG (black curves A and a), RG (red curves C and c) and graphite of mixed ABA and ABC stacking (blue curves B and b), before (c) and after (d) encapsulation. Laser wavelength, 532 nm. e, ρxx as a function of D for Hall bar devices made using domains at point b (light blue) and point c (red), respectively, T = 1.6 K. Inset, optical micrograph of the devices before shaping them into the Hall bar geometry. f, g, Resistivity maps ρxx(nt, nb) of graphite with ABC stacking (f) and mixed stacking (g); T = 1.6 K, B = 0 T.
Extended Data Fig. 2 Band structures of multilayer RG with stacking faults.
a, Schematic of twin-boundary defect. b, c, Calculated spectra for the ABCABCABACBACBACBA sequence at positive (b) and negative (c) D. d, Schematic of a buried Bernal stacking fault ABCBCA. e, f, Calculated band structure for such a defect: ABCABCABABCABCABCA sequence at positive (e) and negative (f) D. g, Schematic of surface stacking fault ABCAC. h, i, Spectra for the ABCABCABCABCABCABA sequence at positive (h) and negative (i) D. In all the calculations we used D = ±1 V nm−1. See Methods section ‘Possibility of stacking faults’ for details of nomenclature used in a, d, g. E is the band energy, px is the in-plane momentum, and pc = γ1/v, where v is the Dirac velocity.
Extended Data Fig. 3 The quantum Hall effect in thin RG.
a, Hall resistivity ρxy (red curve) and longitudinal resistivity ρxx (black curve) as a function of magnetic field B measured at 20 mK for the same device as in main text Fig. 3 (device 1); n = 2.3 × 1012 cm−2, D = 0 V nm−1. b, ρxy and ρxx as a function of n for the same device as in a; D = 0, B = 10 T, T = 20 mK.
Extended Data Fig. 4 Landau levels from surface states of multilayer RG.
a, Calculated free-particle spectrum. b, Conductivity map σxx(nt, nb) for 3-nm-thick RG (device 1) measured at B = 9 T and T = 20 mK. Note that, for two independent surfaces, LLs should form sets of horizontal and vertical lines. The observed behaviour suggests that top and bottom surfaces of our RG devices are nearly independent 2D systems. c, Landau fan σxx(n, B) for device 5 (3.3-nm-thick RG); D = 0, T = 0.25 K. d, Differential dρxx/dν(ν, B) map on the electron side (same device as in c). The red arrows indicate LL crossings. e, σxx(nb, B) for device 8 (7.2-nm-thick RG) measured at T = 1.7 K. f, σxx(n, B) for device 4 (16.5-nm-thick RG) at D = 0 and T = 0.25 K.
Extended Data Fig. 5 Single-gate (D ≠ 0) Landau fan diagrams highlighting the robust ν = −N quantum Hall state in N-layer-thick RG.
a, Conductivity map σxy(ν, B) for 7-layer-thick RG (device 7). b, Conductivity map σxx(ν, B) for 9-layer-thick RG (device 1). c, σxx(ν, B) for 11-layer-thick RG (device 6).
Extended Data Fig. 6 Insulating states and hysteretic behaviour in multilayer RG.
a, b, Additional data for 3.3-nm-thick RG (device 5, same as in main text Fig. 4a, b). a, Main panel, temperature dependence of ρxx(n) around the insulating state, B = 0 T. Inset, Arrhenius plot for the peak resistivity, indicating the presence of a bandgap of about 2–3 meV. The y axis shows peak resistivity, and red line indicates the fit. b, Main panel, histogram of the conductivity values found on the hysteretic curves σxx(n), such as those shown in the inset. Eighty-three such curves were used to make the histogram, where data from forward and backward sweeps are plotted in blue and red, respectively. D = 0, T = 250 mK, B = 0. c, Hysteresis (shaded red) in ρxx(B) observed in device 7 (2.3-nm-thick RG) at the charge neutrality point; d, hysteresis (shaded red) in ρxx(n) at B = 5 T. For c and d, T = 250 mK. e–g, Hysteretic behaviour of device 1 for different cooling cycles. No noticeable hysteresis was found for the first cooling event (e). Hysteresis in ρxx(n) (f) and ρxx(D) (g) is clearly seen after another cooling. Solid (dashed) lines indicate positive (negative) sweep directions and the coloured areas highlight the difference between the sweep directions. T = 20 mK; B = 0 T.
Extended Data Fig. 7 Stacking order of device 6 at different fabrication stages.
a, Optical image of the graphite flake (left) and the corresponding Raman map with a step size of 0.8 μm × 0.8 μm (right). Scale bar, 10 μm. b, Optical image of the graphite flake encapsulated by hBN (left) and the corresponding Raman map with a step size of 0.7 μm × 0.7 μm (right). Scale bar, 10 μm. c, Optical image of the finished Hall bar (left) and the corresponding Raman map with a step size of 0.5 μm × 0.5 μm (right). Scale bar, 4 μm. The colour coding of the Raman maps in a–c indicates the ratio of the integrated area of the low-frequency component (ranging around 2,635–2,665 cm−1) to that of the high-frequency component (ranging around 2,665–2,695 cm−1) of the graphite Raman 2D band. The coloured dots in a–c mark the positions where the Raman spectra shown in e were taken. d, Optical image showing that the Hall bar device is made from the ABC stacked region. Scale bar, 10 μm. e, Typical 2D Raman peaks of RG (dots a, c and d) and of graphite of mixed ABA and ABC stacking (dot b). Laser excitation wavelength, 633 nm.
Extended Data Fig. 8 Temperature dependence of resistivity.
a, ρxx as a function of T at zero gate doping for RG device 4 with a thickness of 16.5 nm (blue solid curve), for RG device 5 with a thickness of 3.3 nm (red solid curve), and for 6-nm HG (grey dashed line). b, Same data as a but plotted on a log scale. While cooling down, ρxx of RG first increases for T > Tc, and then decreases, in sharp contrast to the monotonic decrease of ρxx for HG. The critical temperature Tc decreases with increasing thickness of RG. Besides the presence of Tc, ρxx of the 3.3-nm RG device 5 shows a sharp increase for T < 6 K owing to the phase transition to the insulating state.
Extended Data Fig. 9 Bandgap opening by displacement field.
a, Band dispersion of RG under an applied displacement field; bandgap \(\mathop{\varDelta }\limits^{ \sim }\) is masked by a bandwidth of 2γ4γ1/γ0 such that only the effective gap \(\varDelta \,=\,\mathop{\varDelta }\limits^{ \sim }-2{\gamma }_{4}{\gamma }_{1}/{\gamma }_{0}\) is visible in transport measurements. b, Calculated dependence of \(\mathop{\varDelta }\limits^{ \sim }\) and Δ on displacement field for N = 9 layers.
Rights and permissions
About this article
Cite this article
Shi, Y., Xu, S., Yang, Y. et al. Electronic phase separation in multilayer rhombohedral graphite. Nature 584, 210–214 (2020). https://doi.org/10.1038/s41586-020-2568-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2568-2
This article is cited by
-
Fractional quantum anomalous Hall effect in multilayer graphene
Nature (2024)
-
Rhombohedral graphene goes correlated at four or five layers
Nature Nanotechnology (2024)
-
Ferroelectric and spontaneous quantum Hall states in intrinsic rhombohedral trilayer graphene
Nature Physics (2024)
-
Correlated insulator and Chern insulators in pentalayer rhombohedral-stacked graphene
Nature Nanotechnology (2024)
-
Layer-polarized ferromagnetism in rhombohedral multilayer graphene
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.