Abstract
When miniaturizing fluidic circuitry, the solid walls of the fluid channels become increasingly important1 because they limit the flow rates achievable for a given pressure drop, and they are prone to fouling2. Approaches for reducing the wall interactions include hydrophobic coatings3, liquid-infused porous surfaces4,5,6, nanoparticle surfactant jamming7, changes to surface electronic structure8, electrowetting9,10, surface tension pinning11,12 and use of atomically flat channels13. A better solution may be to avoid the solid walls altogether. Droplet microfluidics and sheath flow achieve this but require continuous flow of the central liquid and the surrounding liquid1,14. Here we demonstrate an approach in which aqueous liquid channels are surrounded by an immiscible magnetic liquid, both of which are stabilized by a quadrupolar magnetic field. This creates self-healing, non-clogging, anti-fouling and near-frictionless liquid-in-liquid fluidic channels. Manipulation of the field provides flow control, such as valving, splitting, merging and pumping. The latter is achieved by moving permanent magnets that have no physical contact with the liquid channel. We show that this magnetostaltic pumping method can be used to transport whole human blood with very little damage due to shear forces. Haemolysis (rupture of blood cells) is reduced by an order of magnitude compared with traditional peristaltic pumping, in which blood is mechanically squeezed through a plastic tube. Our liquid-in-liquid approach provides new ways to transport delicate liquids, particularly when scaling channels down to the micrometre scale, with no need for high pressures, and could also be used for microfluidic circuitry.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data for Figs. 2, 3 and 4 (and Extended Data figures containing data graphs) are provided with the paper. Any other data that support the findings of this study are available on the Zenodo data repository, https://doi.org/10.5281/zenodo.3603029
Code availability
The Python code for calculating magnetic fields is available on the Zenodo data repository, https://doi.org/10.5281/zenodo.3603029
References
Tabeling, P. Introduction to Microfluidics (Oxford, 2005).
Mukhopadhyay, R. When microfluidic devices go bad. Anal. Chem. 77, 429A–432A (2005).
Zhao, B., Moore, J. S. & Beebe, D. J. Surface-directed liquid flow inside microchannels. Science 291, 1023–1026 (2001).
Wong, T.-S. et al. Bioinspired self-repairing slippery surfaces with pressure-stable omniphobicity. Nature 477, 443–447 (2011).
Wang, W. et al. Multifunctional ferrofluid-infused surfaces with reconfigurable multiscale topography. Nature 559, 77–82 (2018).
Leslie, D. C. et al. A bioinspired omniphobic surface coating on medical devices prevents thrombosis and biofouling. Nat. Biotechnol. 32, 1134–1140 (2014).
Forth, J. et al. Reconfigurable printed liquids. Adv. Mater. 30, 1707603 (2018).
Secchi, E. et al. Massive radius-dependent flow slippage in carbon nanotubes. Nature 537, 210–213 (2016).
Banerjee, A., Kreit, E., Liu, Y., Heikenfeld, J. & Papautsky, I. Reconfigurable virtual electrowetting channels. Lab Chip 12, 758 (2012).
Choi, K., Ng, A. H. C., Fobel, R. & Wheeler, A. R. Digital microfluidics. Annu. Rev. Anal. Chem. 5, 413–440 (2012).
Lee, W. C., Heo, Y. J. & Takeuchi, S. Wall-less liquid pathways formed with three-dimensional microring arrays. Appl. Phys. Lett. 101, 114108 (2012).
Walsh, E. J. et al. Microfluidics with fluid walls. Nat. Commun. 8, 816 (2017).
Keerthi, A. et al. Ballistic molecular transport through two-dimensional channels. Nature 558, 420–424 (2018).
Shang, L., Cheng, Y. & Zhao, Y. Emerging droplet microfluidics. Chem. Rev. 117, 7964–8040 (2017).
Zhao, W., Cheng, R., Miller, J. R. & Mao, L. Label-free microfluidic manipulation of particles and cells in magnetic liquids. Adv. Funct. Mater. 26, 3916–3932 (2016).
Coey, J. M. D., Aogaki, R., Byrne, F. & Stamenov, P. Magnetic stabilization and vorticity in submillimeter paramagnetic liquid tubes. Proc. Natl Acad. Sci. USA 106, 8811–8817 (2009).
Caravan, P., Ellison, J. J., McMurry, T. J. & Lauffer, R. B. Gadolinium(iii) chelates as MRI contrast agents: structure, dynamics, and applications. Chem. Rev. 99, 2293–2352 (1999).
Ferrand, J., Favreau, L., Joubaud, S. & Freyssingeas, E. Wetting effect on Torricelli’s law. Phys. Rev. Lett. 117, 248002 (2016).
Rosensweig, R. E. Ferrohydrodynamics (Dover, 2014).
Posocco, P. et al. Interfacial tension of oil/water emulsions with mixed non-ionic surfactants: comparison between experiments and molecular simulations. RSC Adv. 6, 4723–4729 (2016).
Owusu Apenten, R. K. & Zhu, Q.-H. Interfacial parameters for selected Spans and Tweens at the hydrocarbon–water interface. Food Hydrocoll. 10, 27–30 (1996).
Byrnes, J. et al. Hemolysis during cardiac extracorporeal membrane oxygenation: a case-control comparison of roller pumps and centrifugal pumps in a pediatric population. ASAIO J. 57, 456–461 (2011).
Omar, H. R. et al. Plasma free hemoglobin is an independent predictor of mortality among patients on extracorporeal membrane oxygenation support. PLoS ONE 10, e0124034 (2015).
Dalton, H. J. et al. Factors associated with bleeding and thrombosis in children receiving extracorporeal membrane oxygenation. Am. J. Respir. Crit. Care Med. 196, 762–771 (2017).
Valladolid, C., Yee, A. & Cruz, M. A. von Willebrand factor, free hemoglobin and thrombosis in ECMO. Front. Med. 5, 228 (2018).
Wilson, A. M. M. M. et al. Hemolysis risk after packed red blood cells transfusion with infusion pumps. Rev. Lat. Am. Enfermagem 26, e3053 (2018).
Prahl, S. Optical absorption of hemoglobin. Oregon Medical Laser Center https://omlc.org/spectra/hemoglobin/index.html (1999).
Baskin, L., Dias, V., Chin, A., Abdullah, A. & Naugler, C. in Accurate Results in the Clinical Laboratory (eds Dasgupta, A. & Sepulveda, J. L.) 19–34 (Elsevier, 2013).
Jaouen, P., Vandanjon, L. & Quéméneur, F. The shear stress of microalgal cell suspensions (Tetraselmis suecica) in tangential flow filtration systems: the role of pumps. Bioresour. Technol. 68, 149–154 (1999).
Kamaraju, H., Wetzel, K. & Kelly, W. J. Modeling shear-induced CHO cell damage in a rotary positive displacement pump. Biotechnol. Prog. 26, 1606–1615 (2010).
Vázquez-Rey, M. & Lang, D. A. Aggregates in monoclonal antibody manufacturing processes. Biotechnol. Bioeng. 108, 1494–1508 (2011).
Wang, S. et al. Shear contributions to cell culture performance and product recovery in ATF and TFF perfusion systems. J. Biotechnol. 246, 52–60 (2017).
Nesta, D. et al. Aggregation from shear stress and surface interaction: molecule-specific or universal phenomenon? Bioprocess Int. 30, 30–39 (2017).
Hejazian, M., Li, W. & Nguyen, N.-T. Lab on a chip for continuous-flow magnetic cell separation. Lab Chip 15, 959–970 (2015).
Eijkel, J. C. T. & van den Berg, A. Nanofluidics: what is it and what can we expect from it? Microfluid. Nanofluidics 1, 249–267 (2005).
Bocquet, L. & Charlaix, E. Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 39, 1073–1095 (2010).
Bocquet, L. & Tabeling, P. Physics and technological aspects of nanofluidics. Lab Chip 14, 3143–3158 (2014).
Evans, D. F. The determination of the paramagnetic susceptibility of substances in solution by nuclear magnetic resonance. J. Chem. Soc. 1959, 2003–2005 (1959).
Coey, J. M. D. Magnetism and Magnetic Materials (Cambridge Univ. Press, 2010).
Sastri, V. R., Perumareddi, J. R., Rao, V. R., Rayudu, G. V. S. & Bünzli, J.-C. G. Modern Aspects of Rare Earths and their Complexes (Elsevier, 2003).
Cugat, O., Byrne, R., McCaulay, J. & Coey, J. M. D. A compact vibrating-sample magnetometer with variable permanent magnet flux source. Rev. Sci. Instrum. 65, 3570–3573 (1994).
Wysin, G. M. Demagnetization Fields (Kansas State Univ., 2012); https://www.phys.k-state.edu/personal/wysin/notes/demag.pdf.
Furlani, E. P. Permanent Magnet and Electromechanical Devices (Academic, 2001).
Yang, Z. J., Johansen, T. H., Bratsberg, H., Helgesen, G. & Skjeltorp, A. T. Potential and force between a magnet and a bulk Y1Ba2Cu3O7−δ superconductor studied by a mechanical pendulum. Supercond. Sci. Technol. 3, 591 (1990).
Camacho, J. M. & Sosa, V. Alternative method to calculate the magnetic field of permanent magnets with azimuthal symmetry. Rev. Mex. Fis. E 59, 8–17 (2013).
Schindelin, J. et al. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682 (2012).
Daerr, A. & Mogne, A. Pendent_Drop: An ImageJ plugin to measure the surface tension from an image of a pendent drop. J. Open Res. Softw. 4, e3 (2016).
Marone, F. & Stampanoni, M. Regridding reconstruction algorithm for real-time tomographic imaging. J. Synchrotron Radiat. 19, 1029–1037 (2012).
Acknowledgements
We acknowledge the support of the University of Strasbourg Institute for Advanced Studies (USIAS) Fellowship, the ‘Chaire Gutenberg’ of the Région Alsace (J.M.D.C.), the French National Research Agency (ANR) through the Programme d’Investissement d’Avenir under contract ANR-11-LABX-0058_NIE within the Investissement d’Avenir programme ANR-10-IDEX-0002-02, and SATT Conectus funding. This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 766007. We acknowledge the Paul Scherrer Institut for provision of synchrotron radiation beamtime at beamline TOMCAT of the SLS. We thank H. Boping of San Huan Corporation for giving us thin magnetic bilayer sheets. We thank F. Chevrier for technical support, and the staff of the STnano nanofabrication facility for help in sample fabrication. We thank N. Matoussevitch for the synthesis of ferrofluids. We thank F. Sacarelli and G. Formon for additional AAS measurements, A. Cebers of the University of Latvia Riga for the use of ANSYS 18, and S. Potier for advice on the project.
Author information
Authors and Affiliations
Contributions
J.M.D.C., B.D. and T.M.H. conceived and initiated the project. T.A. and P.D. performed most of the experiments and modelling. T.A., J.M.D.C., B.D., P.D. and T.M.H. designed the microfluidics set-ups. A.A.D. performed slip length experiments and modelling. P.D. carried out the magnetic modelling. A.S. developed and synthesized Magoil. L.G. characterized liquid and pumping properties. A.B. led the X-ray tomography experiments. T.A, C.B., T.M.H. and P.H.M. designed and conducted the blood experiments. T.A., J.M.D.C., B.D., P.D. and T.M.H. drafted the manuscript. All authors discussed and contributed to the paper in its final form.
Corresponding author
Ethics declarations
Competing interests
T.M.H. holds shares in Qfluidics, a company devoted to the commercialization of the liquid tube technology presented in this work. P.D., B.D., J.M.D.C. and T.M.H. are co-inventors on patents protecting the technology (WO2018134360A1, pending) for which all parts of the manuscripts are covered.
Additional information
Peer review information Nature thanks Emmanuel Delamarche and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Adaptability of antitube topologies to arbitrary magnetic fields.
a, b, X-ray transmission images of an antitube of water inside a ferrofluid for cuboid magnets (6 × 6 × 50 mm) with 6-mm gap (a); and matching arc magnets of height 20 mm, 3.5-mm gap, and inner and outer diameter pairs of: ID 25 mm, OD 28.5 mm; and ID 33 mm, OD 36.5 mm (b). c–f, Antitube cross-sections using non-quadrupolar fields: the magnetic field calculation (c) and experimental cross-section (d) for a four-magnet arrangement; and the magnetic field calculation (e) and experimental cross-section (f) for a six-magnet arrangement. Scale bar, 3 mm. See Supplementary Videos 5, 6. g, Side view of a 1-m-long water antitube (d = 2 mm), which allows light to pass throughout, showing the continuous water phase.
Extended Data Fig. 2 Magoil synthesis and optical absorption properties.
a, Magoil synthesis reaction scheme. DMF, dimethylformamide; EtOH, ethanol. b, UV–vis absorption spectrum of Ho3+-based paramagnetic Magoil.
Extended Data Fig. 3 Process steps involved in X-ray and optical imaging of antitubes in ferrofluids.
a, b, Typical quadrupole assemblies used for X-ray measurements. c, Inverted transmission X-ray image. d, Transmission averaged along the channel. e, Background-corrected transmission through the water antitube fitted with a Gaussian peak function. f, Optical image of a sub-100-μm water antitube in an EMG900 ferrofluid (double surfactant). g, Intensity profile across the microfluidic channel in the vicinity of the water antitube. The profile is column-averaged along the length of microfluidic channel.
Extended Data Fig. 4 Antitube stability and shear resistance under flow.
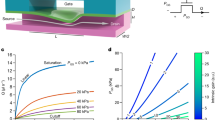
a, b, The threshold flow rate for antitube diameters (a) and areas (b). c, Relative dilation of an antitube in APG311 ferrofluid with a quadrupolar gap, w, of 10 mm under flow and with the outlet closed. d, Side view through the antitubes under static conditions with no flow (outlet closed) for two magnet gaps at equilibrium (0 bar) and under 0.9-bar pressure. e, Normalized velocity profile inside honey using equations (1) and (2), corresponding to data in Fig. 2d. Inset shows velocity profile in both honey and ferrofluid. f, Concentration of Fe found in water after pumping through three different antitube diameters for three flow rates with and without an extra magnet on the outlet flow. Blank tests for pure water give the grey background threshold detection. Values are averages of six samples, error bars are standard deviations.
Extended Data Fig. 5 Flows in antitubes and surrounding ferrofluid using computational fluid dynamics.
a–d, Contour plots from numerical simulations of a honey antitube in EMG900 ferrofluid under a flow rate of 175 μl min−1 for two cases: first, the semi-infinite case with no inlet effects (a, b); second, the finite case including inlet effects with the ferrofluid contours matching those found by experiment (c, d) (compare with Extended Data Fig. 1a). The plots are (a, c) isometric pressure contours for at the outlets; note the different colourmaps for the pressure inside the ferrofluid versus inside the antitube; (b, d) velocity vector field at the outlets. e, f, Geometries used in the derivation of equations (1)–(4). e, Cross-section of liquid tube system considered in derivation of equilibrium diameter equation (3) (see Methods), with four different flow regions consisting of: I, honey; II, a parallel flow of ferrofluid; III, a counterflow of ferrofluid; and IV, a fictitious region to define the radial distance x at which the flow velocity becomes zero. Thus, the slip length for a flow of honey is b = x – R, where tf is the thickness of the ferrofluid, n is the thickness of region with shear flow and R is the radius of the honey tube. f, 2D geometry of four bar magnets in a quadrupolar configuration considered in the derivation of linear and saturation models for the equilibrium tube diameter (see Methods and Supplementary Information). The hatched region denotes the ferrofluid, and the white region in the centre is the contained liquid tube.
Extended Data Fig. 6 Demonstration of photo-polymerization and pumping functionality in antitubes.
a, A scheme of the fluidic chip used for the extrusion of a photopolymer resin and its photopolymerization by 405-nm laser light during extrusion. b, c, Photos of polymerized tubes extruded in (b) an aqueous HoCl3 solution, and (c) an aqueous MnCl2 solution. The diameter of the tubes decreased as the magnet gap decreased, and those photopolymerized in Ho3+ were smaller, as Ho3+ has higher magnetic susceptibility than Mn2+. d, Isometric-view of a six-spoke magnetostaltic pump (see Supplementary Video 11). e, Slow rotation (2 rpm) leads to pulsed flow, whereas fast rotation (14 rpm) produces a smoother flow. f, The average flow rate and standard deviation versus rotation rate ω. g, The magnetic configuration for an antitube (section nearer the viewer) and a pinching region (further section) using magnets (6 × 6 × 50 mm) with a gap of 6 mm. h, Isosurface plot of the calculated magnetic field for g. The weak field region where water can reside is highlighted in white. A water antitube created by the quadrupolar arrangement (left half) is disrupted at the interface between two regions. The field created by the pinching geometry has a field strength of 0.5 T at the centre of magnets (represented by the dark blue colour). i, Top view of the Qpump based on this principle. The orientation of magnetization for the arc segments is radially outward (red) or inward (blue). j, x–y contour plot of the calculated magnetic field along the z-axis centre of the Qpump.
Extended Data Fig. 7 Comparison of platelet and whole blood quality in peristaltic and magnetostaltic pumping.
a–c, Representative SEM images of platelets: after peristaltic pumping (a); platelets from control blood (b); and platelets from blood after Qpump pumping (c). No major morphological change due to the activation of platelets was observed for either type of pump (peristaltic or Qpump). d, A picture of the whole blood in a tube after peristaltic pumping (left), control (middle) and Qpump pumping (right).
Extended Data Fig. 8 Process steps for optical imaging of antitubes in Magoil.
a, b, Optical micrographs of a water antitube in Magoil for a gap width w = 220 μm (a) and w = 307 μm (b). c, d, Greyscale, rotated and inverted images for b and a respectively. e, f, Column average profiles of gap for a and b, respectively. g, h, Gaussian function fits to the background subtracted profiles. Note: the 94-μm antitube is thermodynamically stable, as the image was taken during the extrusion of the water antitube, whereas the 30-μm tube is thermodynamically unstable. After injection, water was then extracted, resulting in a thinning of the tube, which at this diameter collapses into droplets in a matter of minutes.
Supplementary information
Supplementary Information
Additional information is provided in the following sections: I, Langevin and demagnetisation expressions used to correctly determine the magnetic properties of the ferrofluid (M4); II, Remanent magnetisation of permanent magnets for M5; III, 3-D magnetic analytical expressions for M6 IV, Full derivations for equations 1 and 2 (M18); V, Derivation of Equation 3 (M19); VI, Derivation of equation 4 (M20).
Video 1
Extrusion and extraction of water into holmium-based Magoil in a quadrupolar field using two in/outlets. The water is dyed with ink to enhance visibility. Bubbles are removed from the top Magoil–air interface manually.
Video 2
Rupture of an anti-tube in Magoil by a plastic stick, which self-heals without any flow from an external pump.
Video 3
Photocrosslinking of photopolymer resin that was extruded into holmium aqueous solution in a quadrupolar arrangement of magnets.
Video 4
Honey flowing from reservoirs under gravity through three different configurations: an antitube, no tube (that is, air only), and a normal tube of the same diameter.
Video 5
Injection of APG311 ferrofluid into a water-containing thin cell surrounded by four 10×10×10 mm3 cube magnets with the field orientation shown in Extended Data Fig. 1d.
Video 6
Injection of APG311 ferrofluid into a water-containing thin cell surrounded by six 10×10×10 mm3 cube magnets with the field orientation shown in Extended Data Fig. 1f.
Video 7
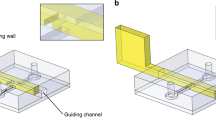
Splitting of water through a free-hanging Y-junction in a ferrofluid. The ferrofluid is held in place by the magnetic field gradient force supplied by the magnets, there is no physical support below it. Water is injected from one input on the left and splits in two on the right.
Video 8
Valving an antitube in ferrofluid using a fifth magnet; upon addition of a magnet the flow stops; upon removal the flow recommences.
Video 9
Animated simulations of 0.15 T isovolume of the magnetic field in a quadrupolar field upon valving with one magnet.
Video 10
Animated simulations of the 0.15 T isovolume of the magnetic field in a quadrupolar field upon valving with two magnets.
Video 11
Non-contact peristaltic pumping using moving valve-points (occlusions) generated by a rotating wheel of valving magnets.
Video 12
The demonstration of pumping water by a Qpump. The outlet was connected to a pressure sensor to measure the pressure generated, showing ~900 mbar of pumping pressure.
Rights and permissions
About this article
Cite this article
Dunne, P., Adachi, T., Dev, A.A. et al. Liquid flow and control without solid walls. Nature 581, 58–62 (2020). https://doi.org/10.1038/s41586-020-2254-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2254-4
This article is cited by
-
Magnetic fluid film enables almost complete drag reduction across laminar and turbulent flow regimes
Communications Physics (2024)
-
Reconfigurable liquid devices from liquid building blocks
Nature Chemical Engineering (2024)
-
Rewritable printing of ionic liquid nanofilm utilizing focused ion beam induced film wetting
Nature Communications (2024)
-
Machining water through laser cutting of nanoparticle-encased water pancakes
Nature Communications (2023)
-
One droplet reaction for synthesis of multi-sized nanoparticles
Nano Research (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.