Abstract
Observing and controlling macroscopic quantum systems has long been a driving force in quantum physics research. In particular, strong coupling between individual quantum systems and mechanical oscillators is being actively studied1,2,3. Whereas both read-out of mechanical motion using coherent control of spin systems4,5,6,7,8,9 and single-spin read-out using pristine oscillators have been demonstrated10,11, temperature control of the motion of a macroscopic object using long-lived electronic spins has not been reported. Here we observe a spin-dependent torque and spin-cooling of the motion of a trapped microdiamond. Using a combination of microwave and laser excitation enables the spins of nitrogen–vacancy centres to act on the diamond orientation and to cool the diamond libration via a dynamical back-action. Furthermore, by driving the system in the nonlinear regime, we demonstrate bistability and self-sustained coherent oscillations stimulated by spin–mechanical coupling, which offers the prospect of spin-driven generation of non-classical states of motion. Such a levitating diamond—held in position by electric field gradients under vacuum—can operate as a ‘compass’ with controlled dissipation and has potential use in high-precision torque sensing12,13,14, emulation of the spin-boson problem15 and probing of quantum phase transitions16. In the single-spin limit17 and using ultrapure nanoscale diamonds, it could allow quantum non-demolition read-out of the spin of nitrogen–vacancy centres at ambient conditions, deterministic entanglement between distant individual spins18 and matter-wave interferometry16,19,20.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Treutlein, P., Genes, C., Hammerer, K., Poggio, M. & Rabl, P. In Cavity Optomechanics: Nano- and Micromechanical Resonators Interacting with Light (eds Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F.) 327–351 (Springer, 2014).
Rabl, P. et al. Strong magnetic coupling between an electronic spin qubit and a mechanical resonator. Phys. Rev. B 79, 041302 (2009).
Leibfried, D., Blatt, R., Monroe, C. & Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).
LaHaye, M. D., Suh, J., Echternach, P. M., Schwab, K. C. & Roukes, M. L. Nanomechanical measurements of a superconducting qubit. Nature 459, 960–964 (2009).
Kolkowitz, S. et al. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 335, 1603–1606 (2012).
Arcizet, O. et al. A single nitrogen-vacancy defect coupled to a nanomechanical oscillator. Nat. Phys. 7, 879–883 (2011).
Lee, D., Lee, K. W., Cady, J. V., Ovartchaiyapong, P. & Jayich, A. C. B. Topical review: spins and mechanics in diamond. J. Opt. 19, 033001 (2017).
O’Connell, A. D. et al. Quantum ground state and single-phonon control of a mechanical resonator. Nature 464, 697–703 (2010).
Treutlein, P., Hunger, D., Camerer, S., Hänsch, T. W. & Reichel, J. Bose-Einstein condensate coupled to a nanomechanical resonator on an atom chip. Phys. Rev. Lett. 99, 140403 (2007).
Mamin, H. J., Poggio, M., Degen, C. L. & Rugar, D. Nuclear magnetic resonance imaging with 90-nm resolution. Nat. Nanotechnol. 2, 301–306 (2007).
Rugar, D., Budakian, R., Mamin, H. J. & Chui, B. W. Single spin detection by magnetic resonance force microscopy. Nature 430, 329–332 (2004).
Kim, P. H., Hauer, B. D., Doolin, C., Souris, F. & Davis, J. P. Approaching the standard quantum limit of mechanical torque sensing. Nat. Commun. 7, 13165 (2016).
Burgess, J. A. J. et al. Quantitative magneto-mechanical detection and control of the Barkhausen effect. Science 339, 1051–1054 (2013).
Hoang, T. M. et al. Torsional optomechanics of a levitated nonspherical nanoparticle. Phys. Rev. Lett. 117, 123604 (2016).
Leggett, A. J. et al. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 59, 1–85 (1987).
Yin, Z. Q., Zhao, N. & Li, T. C. Hybrid opto-mechanical systems with nitrogen-vacancy centers. Sci. China Phys. Mech. Astron. 58, 1–12 (2015).
Conangla, P. G., Schell, A. W., Rica, R. A. & Quidant, R. Motion control and optical interrogation of a levitating single nitrogen vacancy in vacuum. Nano Lett. 18, 3956–3961 (2018).
Rabl, P. et al. A quantum spin transducer based on nanoelectromechanical resonator arrays. Nat. Phys. 6, 602–608 (2010).
Yin, Z., Li, T., Zhang, X. & Duan, L. M. Large quantum superpositions of a levitated nanodiamond through spin-optomechanical coupling. Phys. Rev. A 88, 033614 (2013).
Scala, M., Kim, M. S., Morley, G. W., Barker, P. F. & Bose, S. Matter-wave interferometry of a levitated thermal nano-oscillator induced and probed by a spin. Phys. Rev. Lett. 111, 180403 (2013).
Einstein, A. & Johannes de Haas, W. Experimenteller Nachweis der Ampèreschen Molekularströme. Verh. Deutsch. Physik. Gesellschaft 17, 152–170 (1915).
Alzetta, G., Arimondo, E. & Ascoli, C. Paramagnetic resonance experiments at low fields with angular-momentum detection. Nuovo Cim. B 52, 392–402 (1967).
Arcizet, O., Cohadon, P. F., Briant, T., Pinard, M. & Heidmann, A. Radiation-pressure cooling and optomechanical instability of a micromirror. Nature 444, 71–74 (2006).
Gigan, S. et al. Self-cooling of a micromirror by radiation pressure. Nature 444, 67–70 (2006).
Schliesser, A., Rivière, R., Anetsberger, G., Arcizet, O. & Kippenberg, T. J. Resolved-sideband cooling of a micromechanical oscillator. Nat. Phys. 4, 415–419 (2008).
Barson, M. S. J. et al. Nanomechanical sensing using spins in diamond. Nano Lett. 17, 1496–1503 (2017).
Chang, D. E. et al. Cavity opto-mechanics using an optically levitated nanosphere. Proc. Natl Acad. Sci. USA 107, 1005–1010 (2010).
Romero-Isart, O., Juan, M. L., Quidant, R. & Cirac, J. I. Toward quantum superposition of living organisms. New J. Phys. 12, 033015 (2010).
Huillery, P. et al. Spin-mechanics with levitating ferromagnetic particles. Preprint at http://arxiv.org/abs/1903.09699 (2019).
Wu, M. et al. Nanocavity optomechanical torque magnetometry and radiofrequency susceptometry. Nat. Nanotechnol. 12, 127–131 (2017).
Delord, T. et al. Ramsey interferences and spin echoes from electron spins inside a levitating macroscopic particle. Phys. Rev. Lett. 121, 053602 (2018).
Delord, T., Nicolas, L., Bodini, M. & Hétet, G. Diamonds levitating in a Paul trap under vacuum: measurements of laser-induced heating via NV center thermometry. Appl. Phys. Lett. 111, 013101 (2017).
Delord, T., Nicolas, L., Schwab, L. & Hétet, G. Electron spin resonance from NV centers in diamonds levitating in an ion trap. New J. Phys. 19, 033031 (2017).
Tetienne, J.-P. et al. Magnetic-field-dependent photodynamics of single NV defects in diamond: an application to qualitative all-optical magnetic imaging. New J. Phys. 14, 103033 (2012).
Hebestreit, E., René, R., Frimmer, M. & Novotny, L. Measuring the internal temperature of a levitated nanoparticle in high vacuum. Phys. Rev. A 97, 043803 (2018).
Millen, J., Deesuwan, T., Barker, P. & Anders, J. Nanoscale temperature measurements using non-equilibrium Brownian dynamics of a levitated nanosphere. Nat. Nanotechnol. 9, 425 (2014).
Acknowledgements
We thank R. Blatt, C. Voisin, Y. Chassagneux, E. Baudin and S. Deléglise for discussions.
Author information
Authors and Affiliations
Contributions
T.D. and P.H. contributed equally to this work. T.D., P. H., L.N. and G.H. performed the spin-torque experiments; T.D., P.H. and G.H. analysed the data and performed the modelling with assistance from L.N., and G.H., T. D. and P.H. wrote the manuscript. All authors contributed to the interpretation of the data and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Ashok Ajoy and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Parametric spin-excitation of the librational mode.
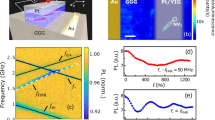
a, Detection principle of the librational modes using microwave parametric excitation (top). Reflected light field amplitude as a function of time for one low-frequency librational mode (170 Hz) at 1 mbar (bottom). b, Spin-mechanical resonance for two different microwave powers: trace i, 20 dBm; trace ii, −10 dBm. c, Reflected light field amplitude as a function of time, for the three microwave frequencies 2.617 GHz (red thin curve), 2.623 GHz (green) and 2.634 GHz (blue) corresponding to the points 1, 2 and 3 in b, respectively. Plain thicker lines show the slow envelope of the fit to the data (see Methods) using two sines at the frequency of the parametrically excited librational mode (480 Hz) and of the closest librational mode (590 Hz) with an amplitude that is 30 times smaller.
Extended Data Fig. 2 Numerical simulations in the nonlinear regime.
a, Effective damping and spring constants as a function of microwave detuning deduced by a numerical fit to the ring-down curves (see Methods). Traces i, ii, iii and iv correspond to increasing microwave Rabi frequencies Ω/2π = 50, 150, 200 and 250 kHz, respectively. b, Evolution of the angle as a function of time after turning on a microwave frequency to the blue of the spin resonance at a time t = 20 ms, showing amplification and finally lasing at t = 120 ms. c, Librational mode velocity as a function of microwave Rabi frequency, for three different values of the spin–lattice relaxation rate 1/T1 = 1, 2 and 3 kHz for traces i, ii and iii, respectively.
Extended Data Fig. 3 Phonon-lasing as a function of time.
Shown is the reflected light field amplitude as a function of time on sudden switch-on of a microwave signal at a time t = 0.02 s to the blue side of the spin transition. The microwave power is above threshold so lasing can be observed after the Brownian motion signal (seen before t = 0.02 s). This curve was used to plot the histogram of Fig. 3C in the main text.
Extended Data Fig. 4 Calibration of sensitivity using NV magnetometry.
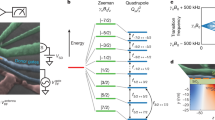
a, Upper panel, mechanically detected spin resonance for three different microwave powers. The dashed line is the locus of the signal minima. Lower panel, angle between the NV axis and magnetic field direction versus NV spin transition frequency. ∆S is the maximal change of the optical signal. ∆θNV is the maximum angle between the NV axis and the magnetic field direction. b, Optical signal as a function of time. c, Left panel, sketch depicting the angular motion of the diamond on magnetization of one class of NV spins using only two angles θx and θy for simplicity. B is the orientation of the magnetic field. Right panel, angular trajectory represented in (θx, θy) space. We note O is the particle orientation without NV magnetization (Mz = 0). The red (green) line is the trajectory in the isotropic (anisotropic) case (see Methods). θd is the detected angle. d, Power spectra of the librational Brownian motion for two different speckle alignments taken with a resolution bandwidth of 1 Hz. The red curve shows all three librational modes. For the blue curve, the detection is tuned to be mainly sensitive to the mode with the highest confinement frequency. The latter detection setting is used for the data shown in a and b.
Extended Data Fig. 5 Measurement of spin polarization rates.
a, Sequences employed to measure the laser induced polarization rate to the ground state (i) and to measure the microwave induced polarization rate to the magnetic state \({m{\prime} }_{{\rm{s}}}=-1\) (ii). The laser is kept on at all times for both sequences. b, Trace i shows the photoluminescence (PL) rate at a time τ after having turned off the microwave signal. An exponential fit to the data gives a laser polarization time of 300 μs. Trace ii shows the photoluminescence rate at a time τ after having turned on the microwave signal. The polarization time to the magnetic state is here 124 μs.
Extended Data Fig. 6 Particle angle dynamics for different microwave detunings in the bistable regime.
a–f, Left panel, experimental observation of the reflected signal amplitude as a function of time for microwave frequencies (in GHz) of 2.8000 (a), 2.8010 (b), 2.8020 (c), 2.8030 (d), 2.8035 (e), 2.8040 (f), tuned to the red of the spin transition. Right panel, histogram showing the number of counts within each bin.
Supplementary information
Supplementary Information
This supplementary file details the theory behind the observations, both on the spin-cooling and phonon lasing effects.
Rights and permissions
About this article
Cite this article
Delord, T., Huillery, P., Nicolas, L. et al. Spin-cooling of the motion of a trapped diamond. Nature 580, 56–59 (2020). https://doi.org/10.1038/s41586-020-2133-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2133-z
This article is cited by
-
Quantum rotations of nanoparticles
Nature Reviews Physics (2021)
-
Quantum electromechanics with levitated nanoparticles
npj Quantum Information (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.