Abstract
Attosecond pulses are central to the investigation of valence- and core-electron dynamics on their natural timescales1,2,3. The reproducible generation and characterization of attosecond waveforms has been demonstrated so far only through the process of high-order harmonic generation4,5,6,7. Several methods for shaping attosecond waveforms have been proposed, including the use of metallic filters8,9, multilayer mirrors10 and manipulation of the driving field11. However, none of these approaches allows the flexible manipulation of the temporal characteristics of the attosecond waveforms, and they suffer from the low conversion efficiency of the high-order harmonic generation process. Free-electron lasers, by contrast, deliver femtosecond, extreme-ultraviolet and X-ray pulses with energies ranging from tens of microjoules to a few millijoules12,13. Recent experiments have shown that they can generate subfemtosecond spikes, but with temporal characteristics that change shot-to-shot14,15,16. Here we report reproducible generation of high-energy (microjoule level) attosecond waveforms using a seeded free-electron laser17. We demonstrate amplitude and phase manipulation of the harmonic components of an attosecond pulse train in combination with an approach for its temporal reconstruction. The results presented here open the way to performing attosecond time-resolved experiments with free-electron lasers.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Raw data were generated at the FERMI large-scale facility. Derived data supporting the findings of this study are available from the corresponding author on reasonable request.
References
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Corkum, P. B. & Krausz, F. Attosecond science. Nat. Phys. 3, 381–387 (2007).
Kapteyn, H., Cohen, O., Christov, I. & Murnane, M. Harnessing attosecond science in the quest for coherent X-rays. Science 317, 775–778 (2007).
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Kienberger, R. et al. Atomic transient recorder. Nature 427, 817–821 (2004).
Tzallas, P., Charalambidis, D., Papadogiannis, N. A., Witte, K. & Tsakiris, G. D. Direct observation of attosecond light bunching. Nature 426, 267–271 (2003).
Nabekawa, Y. et al. Interferometric autocorrelation of an attosecond pulse train in the single-cycle regime. Phys. Rev. Lett. 97, 153904 (2006).
López-Martens, R. et al. Amplitude and phase control of attosecond light pulses. Phys. Rev. Lett. 94, 033001 (2005).
Gustafsson, E. et al. Broadband attosecond pulse shaping. Opt. Lett. 32, 1353–1355 (2007).
Hofstetter, M. et al. Attosecond dispersion control by extreme ultraviolet multilayer mirrors. Opt. Express 19, 1767–1776 (2011).
Bartels, R. et al. Shaped-pulse optimization of coherent emission of high-harmonic soft X-rays. Nature 406, 164–166 (2000).
Ackermann, W. et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photon. 1, 336–342 (2007).
Emma, P. et al. First lasing and operation of an ängstrom-wavelength free-electron laser. Nat. Photon. 4, 641–647 (2010).
Marinelli, A. et al. Experimental demonstration of a single-spike hard-X-ray free electron-laser starting from noise. Appl. Phys. Lett. 111, 151101 (2017).
Huang, S. et al. Generating single-spike hard X-ray pulses with nonlinear bunch compression in free-electron lasers. Phys. Rev. Lett. 119, 154801 (2017).
Hartmann, N. et al. Attosecond time–energy structure of X-ray free-electron laser pulses. Nat. Photon. 12, 215–220 (2018).
Allaria, E. et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photon. 6, 699–704 (2012).
Mairesse, Y. et al. Attosecond synchronization of high-harmonic soft X-rays. Science 302, 1540–1543 (2003).
Schulz, S. et al. Femtosecond all-optical synchronisation of an X-ray free-electron laser. Nat. Commun. 6, 5938 (2015).
Danailov, M. B. et al. Towards jitter-free pump-probe measurements at seeded free electron laser facilities. Opt. Express 22, 12869–12879 (2014).
Prince, K. C. et al. Coherent control with a short-wavelength free-electron laser. Nat. Photon. 10, 176–179 (2016).
Iablonskyi, D. et al. Observation and control of laser-enabled Auger decay. Phys. Rev. Lett. 119, 073203 (2017).
Takahashi, E. J. et al. Attosecond nonlinear optics using gigawatt-scale isolated attosecond pulses. Nat. Commun. 4, 2691 (2013).
Nayak, A. et al. Multiple ionization of argon via multi-XUV-photon absorption induced by 20-GW high-order harmonic laser pulses. Phys. Rev. A 98, 023426 (2018).
Zholents, A. A. Method of an enhanced self-amplified spontaneous emission for x-ray free electron lasers. Phys. Rev. Spec. Top. Accel. Beams 8, 040701 (2005).
Thompson, N. R. & McNeil, B. W. J. Mode locking in a free-electron laser amplifier. Phys. Rev. Lett. 100, 203901 (2008).
Ribič, P. R. et al. Coherent soft X-ray pulses from an echo-enabled harmonic generation free-electron laser. Nat. Photon. 13, 555–561 (2019).
Hemsing, E. et al. Soft X-ray FEL Seeding Studies for LCLS-II: Task Force Status Report. A White Paper by SLAC and LBNL. Technical Note SLAC-TN-19-001 (SLAC, 2019); available at https://www.slac.stanford.edu/pubs/slactns/tn06/slac-tn-19-001.pdf (2019).
Grattoni, V. et al. Status of seeding development at sFLASH. In Proc. FEL2017 (eds Bishofberger, K., Carlsten, B. & Schaa, V. R. W.) 136–139 (JACoW, 2018).
Zhao, Z. et al. Status of the SXFEL facility. Appl. Sci. 7, 607 (2017).
Yong, Y. et al. Dalian extreme ultraviolet coherent light source. Chin. J. Lasers 46, 0100005 (2019).
Finetti, P. et al. Pulse duration of seeded free-electron lasers. Phys. Rev. X 7, 021043 (2017).
Zangrando, M. et al. Recent results of PADReS, the Photon Analysis Delivery and REduction System, from the FERMI FEL commissioning and user operations. J. Synchr. Rad. 22, 565–570 (2015).
Reiche, S. Update on the FEL code GENESIS 1.3. In Proc. 36th Int. Free Electron Laser Conf. (FEL’14) (eds Chrin, J., Reiche, S. & Schaa, V. R. W.) TUP019, 403–407 (JACoW, 2014).
Acknowledgements
This project received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 641789 MEDEA and the Italian Ministry of Research (Project FIRB no. RBID08CRXK). K.U. acknowledges support from the X-ray Free Electron Laser Utilization Research Project and the X-ray Free Electron Laser Priority Strategy Program of the Ministry of Education, Culture, Sports, Science and Technology of Japan (MEXT), from the Cooperative Research Program ‘Network Joint Research Center for Materials and Devices: Dynamic Alliance for Open Innovation Bridging Human, Environment and Materials’, from the bilateral project CNR-JSPS ‘Ultrafast science with extreme ultraviolet Free Electron Lasers’, and from the IMRAM project for international co-operation. R.F. and J.M. thank the Swedish Research Council (VR) and the Knut and Alice Wallenberg Foundation for financial support. E.V.G. acknowledges support from the Foundation for the Advancement of Theoretical Physics and Mathematics ‘BASIS’. M. Meyer and T.M. acknowledge support from the Deutsche Forschungsgemeinschaft (DFG) under grant no. SFB925/1. A.A.L. was supported by the US Department of Energy contract no. DE-AC02-76SF00515. Research at Louisiana State University was supported by the US Department of Energy, Office of Science, Basic Energy Sciences, under contract no. de-sc0010431. Portions of this research were conducted with high performance computing resources provided by Louisiana State University (http://www.hpc.lsu.edu) and by Louisiana Optical Network Infrastructure (http://hpc.loni.org). G.S. acknowledges useful discussions about the simulations and the data analysis with T. Pfeifer and M. Kübel. We acknowledge L. Foglia, A. Simoncig and M. Coreno for valuable discussions.
Author information
Authors and Affiliations
Contributions
P.K.M., M. Moioli, D.E., M.D.F., O.P., H.A., P.C., T.M., M. Meyer, S.B., N.I., E.R.S., J.M., T.C., M.D., S.K., H.N.G., D.Y., K.U., K.C.P., C.G. and C.C. contributed to data acquisition and to data analysis. L.G., E.A., G.D.N., C.S., G.P. and S.S. operated the machine and designed the three and four harmonic generation scheme. A.A.L. contributed to the machine operation. A.D. and M. B. D. designed the beam path for the NIR pulse. P.F. designed the mechanics for the recombination mirror. A.D. and C.G. designed the recombination mirror, and the whole set-up was installed by A.D., C.G. and M.D.F. A.D. and M.D.F. designed and installed the beam dump diagnostic system for alignment of the collinear configuration. M.D.F., O.P. and C.C. prepared the end station. R.B., G.K., C.E.S.D.R. and F.B. developed the analysis tools used during beamtime. M.R. contributed to the preliminary development of the simulation codes. M.L., J.E.B. and K.J.S. performed the TDSE calculations. R.J.S. and R.F. constructed and operated the magnetic bottle electron spectrometer. A.N.G.-G. and E.V.G. developed the perturbation-theory approach and derived the atomic phase contributions. C.C. and G.S. conceived the idea of the experiment. G.S. developed the numerical code for the SFA simulations. P.K.M. developed the numerical code for the correlation analysis. P.K.M., C.C. and G.S. analysed the experimental data and performed the simulations. G.S. supervised the work. P.K.M., A.N.G.-G., E.V.G., C.C. and G.S. wrote the manuscript, which was discussed and agreed by all coauthors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Eduard Prat Costa, Makina Yabashi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
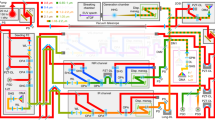
Extended Data Fig. 1 Free-electron laser configuration for the generation of multiple harmonics and experimental setup.
a, b, Configurations of the six undulators (U1–U6) for the generation of three (a) and four (b) harmonics. In the first case, two undulators per harmonic were used, while in the second case, each harmonic was generated by one undulator only. The phase-shifters (PS1–PS5) used to control the relative phase between the harmonics are indicated in yellow for the two configurations. c, d, Typical single-shot photoelectron spectra without (black lines) and with (red lines) the NIR pulse, measured for the three (c) and four (d) harmonic cases. e, Schematic, half-section view of the spectrometer, including the ion flight tube (bottom) and electron flight tube (top). f, Normalized simulated geometrical collection efficiency as a function of polar emission angle for 2–42 eV electrons, using a cylindrical magnet configuration with the pole placed 5 mm away from the interaction region. Electrons were simulated using steps of 5 eV. An emission angle of 0° (180°) corresponds to the axis of the spectrometer in (away from) the direction of the electron detector.
Extended Data Fig. 2 Simulated correlation plots.
Shown are simulated correlation plots (P8,9, P7,8) for different values of Δφ7,8,9 from 0 to 2π in steps of π/4: Δφ7,8,9 = 0 (a), π/4 (b), π/2 (c), 3π/4 (d), π (e), 5π/4 (f), 3π/2 (g), 7π/4 (h) and 2π (i). The intensities of the three harmonics are equal.
Extended Data Fig. 3 Simulated correlation parameter ρ7,8,9.
Evolution of the correlation parameter ρ7,8,9 as a function of the phase difference Δφ7,8,9 simulated using the SFA (red) and the TDSE (blue). The black curve indicates a cosine evolution.
Extended Data Fig. 4 Phase reordering of single-shot sideband intensities.
a, b, Intensity of the sidebands \({{\rm{S}}}_{8,9}^{(-)}\) (a) and \({{\rm{S}}}_{7,8}^{(-)}\) (b) (black points) as a function of the relative phase 3ωNIRτ between the attosecond pulse train and the NIR field. The red curves show sinusoidal fits of the distributions. c, Comparison of the reconstructed attosecond pulse train using the correlation parameter method ρ7,8,9 (black curve) and the ‘reconstruction of attosecond beating by interference of two-photon transitions’ method (red curve) based on the phase differences extracted from the sinusoidal fits. The second method is typically used for the characterization of attosecond pulse trains produced by HHG. The error in the reconstructions is indicated by the shaded areas.
Extended Data Fig. 5 Reconstruction of attosecond pulses for multi-NIR photon transitions.
a–d, Input (black line) and reconstructed (a, red line; b, blue line; c, green line; and d, magenta line) intensity profiles of the attosecond train, corresponding to Fig. 1c–f for phase differences Δφ7,8,9 = 0 (a), π/2 (b), π (c) and 3π/2 (d). e, Reconstruction of attosecond pulses from sideband oscillations for multi-NIR photon transitions for the trace presented in Fig. 1b (input (black line) and reconstructed (blue dotted line) intensity profiles). The intensity of the NIR pulse is INIR = 1.5 × 1011 W cm−2. The relative phases between the harmonics are: φ10 − φ9 = 108°, φ9 − φ8 = 160° and φ8 − φ7 = 8°.
Extended Data Fig. 6 GENESIS 1.3 simulations.
Shown is the attosecond pulse train simulated using the GENESIS 1.3 code: a, complete temporal evolution of the train, and b, magnified view of the attosecond pulses in the train.
Supplementary information
Supplementary Methods
This file contains the Supplementary Methods and additional references.
Rights and permissions
About this article
Cite this article
Maroju, P.K., Grazioli, C., Di Fraia, M. et al. Attosecond pulse shaping using a seeded free-electron laser. Nature 578, 386–391 (2020). https://doi.org/10.1038/s41586-020-2005-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-2005-6
This article is cited by
-
Transient responses of double core-holes generation in all-attosecond pump-probe spectroscopy
Scientific Reports (2024)
-
Acousto-optic modulation of gigawatt-scale laser pulses in ambient air
Nature Photonics (2024)
-
Out-of-equilibrium charge redistribution in a copper-oxide based superconductor by time-resolved X-ray photoelectron spectroscopy
Scientific Reports (2024)
-
Experimental demonstration of attosecond pump–probe spectroscopy with an X-ray free-electron laser
Nature Photonics (2024)
-
Prediction on X-ray output of free electron laser based on artificial neural networks
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.