Abstract
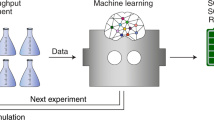
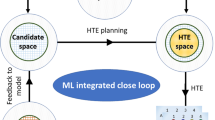
Simultaneously optimizing many design parameters in time-consuming experiments causes bottlenecks in a broad range of scientific and engineering disciplines1,2. One such example is process and control optimization for lithium-ion batteries during materials selection, cell manufacturing and operation. A typical objective is to maximize battery lifetime; however, conducting even a single experiment to evaluate lifetime can take months to years3,4,5. Furthermore, both large parameter spaces and high sampling variability3,6,7 necessitate a large number of experiments. Hence, the key challenge is to reduce both the number and the duration of the experiments required. Here we develop and demonstrate a machine learning methodology to efficiently optimize a parameter space specifying the current and voltage profiles of six-step, ten-minute fast-charging protocols for maximizing battery cycle life, which can alleviate range anxiety for electric-vehicle users8,9. We combine two key elements to reduce the optimization cost: an early-prediction model5, which reduces the time per experiment by predicting the final cycle life using data from the first few cycles, and a Bayesian optimization algorithm10,11, which reduces the number of experiments by balancing exploration and exploitation to efficiently probe the parameter space of charging protocols. Using this methodology, we rapidly identify high-cycle-life charging protocols among 224 candidates in 16 days (compared with over 500 days using exhaustive search without early prediction), and subsequently validate the accuracy and efficiency of our optimization approach. Our closed-loop methodology automatically incorporates feedback from past experiments to inform future decisions and can be generalized to other applications in battery design and, more broadly, other scientific domains that involve time-intensive experiments and multi-dimensional design spaces.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets used in this study are available at https://data.matr.io/1.
Code availability
The CLO code, data and figures associated with this manuscript are available at https://github.com/chueh-ermon/battery-fast-charging-optimization. The data processing and early-prediction code are available at https://github.com/chueh-ermon/BMS-autoanalysis. The charging protocol generation code (automated creation of battery cycler tests) is available at https://github.com/chueh-ermon/automate-Arbin-schedule-file-creation.
References
Tabor, D. P. et al. Accelerating the discovery of materials for clean energy in the era of smart automation. Nat. Rev. Mater. 3, 5–20 (2018).
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547–555 (2018).
Baumhöfer, T., Brühl, M., Rothgang, S. & Sauer, D. U. Production caused variation in capacity aging trend and correlation to initial cell performance. J. Power Sources 247, 332–338 (2014).
Keil, P. & Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—an experimental study with different 18650 high-power cells. J. Energy Storage 6, 125–141 (2016).
Severson, K. A. et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 4, 383–391 (2019).
Schuster, S. F., Brand, M. J., Berg, P., Gleissenberger, M. & Jossen, A. Lithium-ion cell-to-cell variation during battery electric vehicle operation. J. Power Sources 297, 242–251 (2015).
Harris, S. J., Harris, D. J. & Li, C. Failure statistics for commercial lithium ion batteries: a study of 24 pouch cells. J. Power Sources 342, 589–597 (2017).
Ahmed, S. et al. Enabling fast charging—a battery technology gap assessment. J. Power Sources 367, 250–262 (2017).
Liu, Y., Zhu, Y. & Cui, Y. Challenges and opportunities towards fast-charging battery materials. Nat. Energy 4, 540–550 (2019).
Hoffman, M. W., Shahriari, B. & de Freitas, N. On correlation and budget constraints in model-based bandit optimization with application to automatic machine learning. In Proc. 17th Int. Conf. on Artificial Intelligence and Statistics (AISTATS) Vol. 33, 365–374 (Proceedings of Machine Learning Research, 2014); http://proceedings.mlr.press/v33/hoffman14.html.
Grover, A. et al. Best arm identification in multi-armed bandits with delayed feedback. In Proc. 21st Int. Conf. on Artificial Intelligence and Statistics (AISTATS) Vol. 84, 833–842 (Proceedings of Machine Learning Research, 2018); http://proceedings.mlr.press/v84/grover18b.html.
Nikolaev, P. et al. Autonomy in materials research: a case study in carbon nanotube growth. npj Comput. Mater. 2, 16031 (2016).
Ling, J., Hutchinson, M., Antono, E., Paradiso, S. & Meredig, B. High-dimensional materials and process optimization using data-driven experimental design with well-calibrated uncertainty estimates. Integr. Mater. Manuf. Innov. 6, 207–217 (2017).
Balachandran, P. V., Kowalski, B., Sehirlioglu, A. & Lookman, T. Experimental search for high-temperature ferroelectric perovskites guided by two-step machine learning. Nat. Commun. 9, 1668 (2018).
Bédard, A.-C. et al. Reconfigurable system for automated optimization of diverse chemical reactions. Science 361, 1220–1225 (2018).
Granda, J. M., Donina, L., Dragone, V., Long, D.-L. & Cronin, L. Controlling an organic synthesis robot with machine learning to search for new reactivity. Nature 559, 377–381 (2018).
King, R. D. et al. The automation of science. Science 324, 85–89 (2009).
Schneider, G. Automating drug discovery. Nat. Rev. Drug Discov. 17, 97–113 (2018).
Domhan, T., Springenberg, J. T. & Hutter, F. Speeding up automatic hyperparameter optimization of deep neural networks by extrapolation of learning curves. In Proc. 24th Int. Conf. on Artificial Intelligence 3460–3468 (AAAI Press, 2015).
Klein, A., Falkner, S., Springenberg, J. T. & Hutter, F. Learning curve prediction with Bayesian neural networks. In Proc. 2017 Int. Conf. on Learning Representations 1–16 (2017); https://openreview.net/forum?id=S11KBYclx.
Petrak, J. Fast Subsampling Performance Estimates for Classification Algorithm Selection. Technical Report TR-2000-07, 3–14 (Austrian Research Institute for Artificial Intelligence, 2000); http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.28.3305&rep=rep1&type=pdf.
Li, L., Jamieson, K., DeSalvo, G., Rostamizadeh, A. & Talwalkar, A. Hyperband: a novel bandit-based approach to hyperparameter optimization. J. Mach. Learn. Res. 18, 1–52 (2018).
Hutter, F., Hoos, H. H. & Leyton-Brown, K. Sequential model-based optimization for general algorithm configuration. In Proc. 5th Int. Conf. on Learning and Intelligent Optimization 507–523 (Springer, 2011).
Luo, Y., Liu, Y. & Wang, S. Search for an optimal multistage charging pattern for lithium-ion batteries using the Taguchi approach. In Region 10 Conf. (TENCON 2009) 1–5, https://doi.org/10.1109/TENCON.2009.5395823 (IEEE, 2009).
Liu, Y., Hsieh, C. & Luo, Y. Search for an optimal five-step charging pattern for Li-ion batteries using consecutive orthogonal arrays. IEEE Trans. Energ. Convers. 26, 654–661 (2011).
Schindler, S., Bauer, M., Cheetamun, H. & Danzer, M. A. Fast charging of lithium-ion cells: identification of aging-minimal current profiles using a design of experiment approach and a mechanistic degradation analysis. J. Energy Storage 19, 364–378 (2018).
Zou, H. & Hastie, T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B 67, 301–320 (2005).
Keil, P. et al. Calendar aging of lithium-ion batteries. I. Impact of the graphite anode on capacity fade. J. Electrochem. Soc. 163, A1872–A1880 (2016).
Wood, D. L., Li, J. & Daniel, C. Prospects for reducing the processing cost of lithium ion batteries. J. Power Sources 275, 234–242 (2015).
Zimmerman, A. H., Quinzio, M. V. & Monica, S. Adaptive charging method for lithium-ion battery cells. US Patent US6204634B1 (2001).
Park, S., Kato, D., Gima, Z., Klein, R. & Moura, S. Optimal experimental design for parameterization of an electrochemical lithium-ion battery model. J. Electrochem. Soc. 165, A1309–A1323 (2018).
Smith, J. S., Nebgen, B., Lubbers, N., Isayev, O. & Roitberg, A. E. Less is more: sampling chemical space with active learning. J. Chem. Phys. 148, 241733 (2018).
Shahriari, B., Swersky, K., Wang, Z., Adams, R. P. & de Freitas, N. Taking the human out of the loop: a review of Bayesian optimization. Proc. IEEE 104, 148–175 (2016).
Audibert, J.-Y., Bubeck, S. & Munos, R. Best arm identification in multi-armed bandits. In Proc. 23rd Conf. on Learning Theory (COLT) 41–53 (2010); http://certis.enpc.fr/~audibert/Mes%20articles/COLT10.pdf.
Srinivas, N., Krause, A., Kakade, S. M. & Seeger, M. W. Information-theoretic regret bounds for Gaussian process optimization in the bandit setting. IEEE Trans. Inf. Theory 58, 3250–3265 (2012).
Drake, S. J. et al. Measurement of anisotropic thermophysical properties of cylindrical Li-ion cells. J. Power Sources 252, 298–304 (2014).
Çengel, Y. A. & Boles, M. A. Thermodynamics: An Engineering Approach (McGraw-Hill Education, 2015).
Smith, A. J., Burns, J. C., Zhao, X., Xiong, D. & Dahn, J. R. A high precision coulometry study of the SEI growth in Li/graphite cells. J. Electrochem. Soc. 158, A447–A452 (2011).
Zhang, S. S. The effect of the charging protocol on the cycle life of a Li-ion battery. J. Power Sources 161, 1385–1391 (2006).
Kim, J. M. et al. Battery charging method and battery pack using the same. US Patent Application US20160226270A1 (2016).
Lee, M.-S., Song, S.-B., Jung, J.-S. & Golovanov, D. Battery charging method and battery pack using the same. US Patent US9917458B2 (2018).
Notten, P. H. L., Op het Veld, J. H. G. & van Beek, J. R. G. Boostcharging Li-ion batteries: a challenging new charging concept. J. Power Sources 145, 89–94 (2005).
Paryani, A. Low temperature charging of Li-ion cells. US Patent US8552693B2 (2013).
Mehta, V. H. & Straubel, J. B. Fast charging with negative ramped current profile. US Patent US8643342B2 (2014).
Acknowledgements
This work was supported by the Toyota Research Institute through the Accelerated Materials Design and Discovery programme. P.M.A. was supported by the Thomas V. Jones Stanford Graduate Fellowship and the National Science Foundation Graduate Research Fellowship under grant number DGE-114747. A.G. was supported by a Microsoft Research PhD Fellowship and a Stanford Data Science Scholarship. N.P. was supported by the SAIC Innovation Center through the Stanford Energy 3.0 industry affiliates programme. S.J.H. was supported by the Assistant Secretary for Energy Efficiency, Vehicle Technologies Office of the US Department of Energy under the Advanced Battery Materials Research Program. X-ray tomography was performed at the Stanford Nano Shared Facilities, supported by the National Science Foundation under award ECCS-1542152. We thank A. Anapolsky, L. Attia, C. Cundy, J. Hirshman, S. Jorgensen, G. McConohy, J. Song, R. Smith, B. Storey and H. Thaman for discussions.
Author information
Authors and Affiliations
Contributions
P.M.A., N.J., Y.-H.L., M.H.C., N.P. and W.C.C. conceived and conducted the experiments. A.G., T.M.M., B.C. and S.E. developed the Bayesian optimization algorithm and incorporated early outcome predictions into the closed loop. P.M.A. and K.A.S. performed the early-prediction modelling. P.M.A., Z.Y., P.K.H. and M.A. performed data management. P.M.A., A.G., N.J., S.J.H., S.E. and W.C.C. interpreted the results. All authors edited and reviewed the manuscript. R.D.B., S.E. and W.C.C. supervised the work.
Corresponding authors
Ethics declarations
Competing interests
S.E., W.C.C., A.G., T.M.M., N.P. and P.M.A. have filed a patent application related to this work: US Patent Application No. 16/161,790 (16 October 2018).
Additional information
Peer review information Nature thanks Marius Bauer, Matthias Seeger and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Illustrations of early outcome predictor and BO components of CLO.
a, Illustration of early outcome prediction for two cells (A and B) using data from only the first 100 cycles. Two discharge capacity features are generated: the second-cycle discharge capacity, Qd,2, and the difference between the maximum and second-cycle discharge capacities, max(Qd) − Qd,2. Three voltage features are generated: the logarithm of the minimum, variance and the skewness of the difference in voltage curves between cycles 100 and 10. These five features are combined in a linear model to predict the final cycle life, or the number of cycles until the capacity falls below 0.88 A h. The weights and scalings of each feature are determined by training the model on a training set using the elastic net; the weights and scaling values are presented in Supplementary Table 1. See Severson et al.7 and Methods for additional details. b, Illustration of the BO principle. The desired output, cycle life, has a true functional dependence on charging protocol parameters (such as CC1). Here, we show a one-dimensional model (that is, just dependent on one parameter, CC1) for simplicity. By performing Gaussian process regression on the available data, we develop a probabilistic estimate of the true function; our goal is for the estimate to match the true function. The next data point selected is that which maximizes the upper confidence bound (UCB), which is selected by either high uncertainty (exploration) or high predicted value (exploitation). Once this point is selected (right panel), the next point selected is, again, that which maximizes the upper confidence bound.
Extended Data Fig. 2 Cell characterization.
a, b, Voltage versus capacity during rate testing of A123 18650M1A cylindrical cells under charge (a) and discharge (b). The (dis)charge step not under investigation is cycled at 1C to isolate the rate of each step; for example, the charge rate test is performed with 1-C discharge steps. We note that the discharge rate capability is much higher than that of charge. c, d, Battery surface temperature (‘can temperature’) versus capacity during rate testing under charge (c) and discharge (d). The can temperature is measured via a type T thermocouple secured with thermal epoxy. e, f, Overpotential as a function of SOC and C rate (see Methods section ‘Overpotential analysis’ for details of the measurement) for a minimally cycled cell (e) and an aged cell at 80% of nominal capacity (f). The trend lines are linear fits of the overpotential as a function of current at fixed SOC (excluding outliers). We note that both of the relationships are linear (indicating that the rate capability is ohmically limited) and that the SOC dependence is weak, particularly for the minimally cycled cell. The initial internal resistance, averaged over two cells and all four SOCs, is 33 mΩ.
Extended Data Fig. 3 Additional optimization results.
a, b, Mean of the absolute difference in CLO-estimated cycle lives with increasing rounds, expressed as both percentage change (a) and absolute change (b). These changes are relatively small beyond round 2, suggesting that the closed loop can perform well with even smaller time or battery budgets. c, Change in Kendall rank correlation coefficient with increasing rounds. From round 3 to round 4, the ranking of the top protocols shifts, but the cycle lives of these top protocols are similar. d, Distribution of CLO-estimated mean cycle lives after round 4. The mean and standard deviation are 943 cycles and 126 cycles, respectively. e, Correlation between CLO-estimated mean cycle lives and the sum of squared currents, a simplified measure of heat generation (P = I2R). This relationship suggests that minimizing heat generation, as opposed to avoiding lithium plating, may be the operative optimization strategy for these cells under these conditions. f, Standard deviation (σ4,i) versus mean (μ4,i) of the BO predictive distribution over cycle life after round 4. The standard deviation quantifies the uncertainty in the cycle life estimates and is generally low for protocols estimated to have high mean cycle life, since these protocols are probed more frequently. We start with a relatively wide, flat prior (standard deviation 164) and therefore the uncertainty intervals after four rounds are also wide. g, Mean ± standard deviation of the predictive distribution over cycle life after round 4 (μ4,i ± σ4,i) for all charging protocols, sorted by their rank after round 4. The legend indicates the number of repetitions for each protocol (excluding failed batteries).
Extended Data Fig. 4 Means and upper/lower confidence bounds (μk,i ± βkσk,i) on cycle life per round k.
Protocol indices on the x-axis are sorted by rank after round 4. The weighted interval around the estimated mean, βkσk,i = (β0εk)σk,i, weights the protocol-specific standard deviation at round k, σk,i (estimated by the Gaussian process model) with the exploration tradeoff hyperparameter at round k, βk. The upper and lower confidence bounds are plotted for all charging protocols before round 1 (a) and after rounds 1 (b), 2 (c), 3 (d) and 4 (e). The predictive distributions for all charging protocols have identical means and standard deviations before the first round of testing. Because the standard deviations are weighted by βk = β0εk and ε = 0.5, the weighted confidence bounds rapidly decrease with increasing round number, favouring exploitation (examination of protocols with high means). The BO algorithm recommends the 48 protocols with the highest upper bounds (red points); the upper bounds are high either due to high uncertainty (exploration) or high means (exploitation). The algorithm rapidly shifts from exploration to exploitation as εk rapidly shrinks the upper bounds with increasing round index. We note that one protocol per round that should have been selected (that is, with a top-48 upper bound) was not selected owing to a processing error; instead, the protocol with the 49th-highest upper bound was selected.
Extended Data Fig. 5 Mean and standard deviation of the CLO-estimated predicted distribution over cycle lives after round 4.
In this two-dimensional representation, mean estimated cycle life (colour scale) and standard deviation of cycle life (marker size) after round 4 are presented as a function of CC1, CC2 and CC3 (the x axis, y axis and panels a–f, respectively). Panels a–f represent CC3 = 3.6C, 4.0C, 4.4C, 4.8C, 5.2C, 5.6C and 6.0C, respectively. CC4 is represented by the contour lines. Note that the protocols with the highest cycle lives generally have the smallest standard deviations, since these protocols have been tested repeatedly.
Extended Data Fig. 6 Selected protocols for validation.
The three protocols with the highest CLO-estimated mean cycle lives are shown in panels b, c and d. The protocols shown in panels a, f, g and h are approximations of previously proposed battery fast-charging protocols (Extended Data Table 1). The remaining two protocols, shown in panels e and i, were selected to obtain a representative sampling from the entire distribution of CLO-estimated cycle lives. The annotations on each panel represent the cycle lives of each protocol as estimated by CLO (‘CLO’), early outcome prediction from validation (‘Early prediction’), and the final cycle lives from validation (‘Final’). In the annotations, the errors represent the CLO-estimated standard deviation after round 4 (σk,4) for the CLO-estimated cycle lives and the 95% confidence intervals for the early-predicted and final cycle lives from validation (n = 5; n = 4 for the early predictions of 3.6C-6.0C-5.6C-4.755C) (a).
Extended Data Fig. 7 Validation ablation analysis.
We perform pairwise comparisons of the cycle lives of the nine validation protocols, as estimated from three sources: closed-loop estimates after four rounds, early predictions from the validation experiment and final cycle lives from the validation experiment. Panels a–c compare closed-loop estimates to early predictions from validation, panels d–f compare final cycle lives from validation to early predictions from validation, and panels g–i compare final cycle lives from validation to closed-loop estimates. The first column (a, d and g) compares cycle lives averaged on a protocol basis; the second column (b, e and h) compares cycle lives on a battery (cell) basis; and the third column (c, f and i) compares the predicted ranking by cycle life via each method. Orange points represent the top three CLO-estimated protocols, blue points represent protocols inspired by the battery literature (Methods), and green points represent protocols selected to sample the distribution of estimated cycle lives. The error bars represent the 95% confidence intervals (n = 5; n = 4 for the early predictions of 3.6C-6.0C-5.6C-4.755C). The Pearson correlation coefficient and Kendall rank correlation coefficients are displayed for all relevant cycle life and ranking plots, respectively.
Extended Data Fig. 8 Closed-loop performance under resource constraints.
Comparison of the closed loop with and without the Bayesian optimization algorithm (that is, with and without the explore/exploit component) as a function of number of channels and number of rounds in the 224-protocol space, using the first-principles simulator as the ground-truth source for cycle lives. Early prediction is not included. Each point represents the mean of 100 simulations; error bars represent the 95% confidence intervals (n = 100). Early prediction is not incorporated into these simulations. The complete closed loop (that is, with Bayesian optimization) consistently outperforms the closed loop without Bayesian optimization. Bayesian optimization offers the largest advantage when the number of channels is low relative to the number of protocols.
Extended Data Fig. 9 Hyperparameter sensitivity analysis on a cycle life simulator.
The true cycle life of the best charging protocol as estimated by CLO, averaged over ten random seeds, is plotted as a function of the initial exploration constant (β0), the exploration decay factor (ε) and the kernel bandwidth (γ). The values of all other hyperparameters are consistent with the values indicated in the ‘BO hyperparameter optimization’ Methods section and in Supplementary Table 5. Overall, CLO achieves acceptable performance over a range of hyperparameter combinations; the highest-cycle-life protocols as estimated by the best and worst hyperparameter combinations differ by only 60 cycles. In our real-world CLO experiment, the selected hyperparameters are β0 = 5.0, ε = 0.5 and γ = 1; this combination performed well on a variety of simulated parameter spaces and budgets.
Supplementary information
Supplementary Information
This file contains Supplementary Tables 1-6, Supplementary Discussions 1-4 and Supplementary References.
Rights and permissions
About this article
Cite this article
Attia, P.M., Grover, A., Jin, N. et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 578, 397–402 (2020). https://doi.org/10.1038/s41586-020-1994-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-020-1994-5
This article is cited by
-
Sustainable plug-in electric vehicle integration into power systems
Nature Reviews Electrical Engineering (2024)
-
Origin of fast charging in hard carbon anodes
Nature Energy (2024)
-
A cross-scale framework for evaluating flexibility values of battery and fuel cell electric vehicles
Nature Communications (2024)
-
Universal machine learning aided synthesis approach of two-dimensional perovskites in a typical laboratory
Nature Communications (2024)
-
Autonomous closed-loop mechanistic investigation of molecular electrochemistry via automation
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.