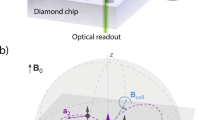
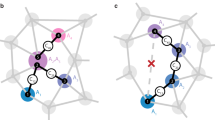
Abstract
Nuclear magnetic resonance (NMR) is a powerful method for determining the structure of molecules and proteins1. Whereas conventional NMR requires averaging over large ensembles, recent progress with single-spin quantum sensors2,3,4,5,6,7,8,9 has created the prospect of magnetic imaging of individual molecules10,11,12,13. As an initial step towards this goal, isolated nuclear spins and spin pairs have been mapped14,15,16,17,18,19,20,21. However, large clusters of interacting spins—such as those found in molecules—result in highly complex spectra. Imaging these complex systems is challenging because it requires high spectral resolution and efficient spatial reconstruction with sub-ångström precision. Here we realize such atomic-scale imaging using a single nitrogen vacancy centre as a quantum sensor, and demonstrate it on a model system of 27 coupled 13C nuclear spins in diamond. We present a multidimensional spectroscopy method that isolates individual nuclear–nuclear spin interactions with high spectral resolution (less than 80 millihertz) and high accuracy (2 millihertz). We show that these interactions encode the composition and inter-connectivity of the cluster, and develop methods to extract the three-dimensional structure of the cluster with sub-ångström resolution. Our results demonstrate a key capability towards magnetic imaging of individual molecules and other complex spin systems9,10,11,12,13.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Rule, G. S. & Hitchens, T. K. Fundamentals of Protein NMR Spectroscopy Vol. 5 (Springer Science & Business Media, 2006).
Mamin, H. et al. Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 339, 557–560 (2013).
Staudacher, T. et al. Nuclear magnetic resonance spectroscopy on a (5-nanometer)3 sample volume. Science 339, 561–563 (2013).
Shi, F. et al. Single-protein spin resonance spectroscopy under ambient conditions. Science 347, 1135–1138 (2015).
Lovchinsky, I. et al. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science 351, 836–841 (2016).
Aslam, N. et al. Nanoscale nuclear magnetic resonance with chemical resolution. Science 357, 67–71 (2017).
Glenn, D. R. et al. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 555, 351–354 (2018).
Smits, J. et al. Two-dimensional nuclear magnetic resonance spectroscopy with a microfluidic diamond quantum sensor. Sci. Adv. 5, eaaw7895 (2019).
Lovchinsky, I. et al. Magnetic resonance spectroscopy of an atomically thin material using a single-spin qubit. Science 355, 503–507 (2017).
Ajoy, A., Bissbort, U., Lukin, M. D., Walsworth, R. L. & Cappellaro, P. Atomic-scale nuclear spin imaging using quantum-assisted sensors in diamond. Phys. Rev. X 5, 011001 (2015).
Kost, M., Cai, J. & Plenio, M. B. Resolving single molecule structures with nitrogen-vacancy centers in diamond. Sci. Rep. 5, 11007 (2015).
Perunicic, V., Hill, C., Hall, L. & Hollenberg, L. A quantum spin-probe molecular microscope. Nat. Commun. 7, 12667 (2016).
Wang, Z.-Y., Haase, J. F., Casanova, J. & Plenio, M. B. Positioning nuclear spins in interacting clusters for quantum technologies and bioimaging. Phys. Rev. B 93, 174104 (2016).
Sushkov, A. et al. Magnetic resonance detection of individual proton spins using quantum reporters. Phys. Rev. Lett. 113, 197601 (2014).
Müller, C. et al. Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 5, 4703 (2014).
Shi, F. et al. Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 10, 21–25 (2014).
Zopes, J. et al. Three-dimensional localization spectroscopy of individual nuclear spins with sub-angstrom resolution. Nat. Commun. 9, 4678 (2018).
Zopes, J., Herb, K., Cujia, K. S. & Degen, C. L. Three-dimensional nuclear spin positioning using coherent radio-frequency control. Phys. Rev. Lett. 121, 170801 (2018).
Sasaki, K., Itoh, K. M. & Abe, E. Determination of the position of a single nuclear spin from free nuclear precessions detected by a solid-state quantum sensor. Phys. Rev. B 98, 121405 (2018).
Abobeih, M. H. et al. One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 9, 2552 (2018).
Yang, Z. et al. Structural analysis of nuclear spin clusters via two-dimensional nanoscale nuclear magnetic resonance spectroscopy. Preprint at https://arxiv.org/abs/1902.05676v2 (2019).
Rosenfeld, E. L., Pham, L. M., Lukin, M. D. & Walsworth, R. L. Sensing coherent dynamics of electronic spin clusters in solids. Phys. Rev. Lett. 120, 243604 (2018).
Knowles, H. S., Kara, D. M. & Atatüre, M. Demonstration of a coherent electronic spin cluster in diamond. Phys. Rev. Lett. 117, 100802 (2016).
Cramer, J. et al. Repeated quantum error correction on a continuously encoded qubit by real-time feedback. Nat. Commun. 7, 11526 (2016).
Pfender, M. et al. High-resolution spectroscopy of single nuclear spins via sequential weak measurements. Nat. Commun. 10, 594 (2019).
Cujia, K., Boss, J., Herb, K., Zopes, J. & Degen, C. Tracking the precession of single nuclear spins by weak measurements. Nature 571, 230–233 (2019).
Slichter, C. Principles of Magnetic Resonance (Springer, 1996).
Bradley, C. E. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Laraoui, A. et al. High-resolution correlation spectroscopy of 13C spins near a nitrogen-vacancy centre in diamond. Nat. Commun. 4, 1651 (2013).
Pfender, M. et al. Nonvolatile nuclear spin memory enables sensor-unlimited nanoscale spectroscopy of small spin clusters. Nat. Commun. 8, 834 (2017).
Maurer, P. C. et al. Room-temperature quantum bit memory exceeding one second. Science 336, 1283–1286 (2012).
Dutt, M. G. et al. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316, 1312–1316 (2007).
Nizovtsev, A. P. et al. Non-flipping 13C spins near an NV center in diamond: hyperfine and spatial characteristics by density functional theory simulation of the C510[NV]H252 cluster. New J. Phys. 20, 023022 (2018).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Toyli, D. M., de las Casas, C. F., Christle, D. J., Dobrovitski, V. V. & Awschalom, D. D. Fluorescence thermometry enhanced by the quantum coherence of single spins in diamond. Proc. Natl Acad. Sci. USA 110, 8417–8421 (2013).
Taminiau, T. H. et al. Detection and control of individual nuclear spins using a weakly coupled electron spin. Phys. Rev. Lett. 109, 137602 (2012).
Kolkowitz, S., Unterreithmeier, Q. P., Bennett, S. D. & Lukin, M. D. Sensing distant nuclear spins with a single electron spin. Phys. Rev. Lett. 109, 137601 (2012).
Zhao, N. et al. Sensing single remote nuclear spins. Nat. Nanotechnol. 7, 657–662 (2012).
Boss, J. M., Cujia, K., Zopes, J. & Degen, C. L. Quantum sensing with arbitrary frequency resolution. Science 356, 837–840 (2017).
Schmitt, S. et al. Submillihertz magnetic spectroscopy performed with a nanoscale quantum sensor. Science 356, 832–837 (2017).
Laraoui, A., Pagliero, D. & Meriles, C. A. Imaging nuclear spins weakly coupled to a probe paramagnetic center. Phys. Rev. B 91, 205410 (2015).
Gullion, T., Baker, D. B. & Conradi, M. S. New, compensated Carr–Purcell sequences. J. Magn. Reson. 89, 479–484 (1990).
Warren, W. S. Effects of arbitrary laser or NMR pulse shapes on population inversion and coherence. J. Chem. Phys. 81, 5437–5448 (1984).
Zhao, N., Hu, J.-L., Ho, S.-W., Wan, J. T. K. & Liu, R. B. Atomic-scale magnetometry of distant nuclear spin clusters via nitrogen-vacancy spin in diamond. Nat. Nanotechnol. 6, 242–246 (2011).
Acknowledgements
We thank V. V. Dobrovitski, T. van der Sar, W. Hahn, M. Scheer and R. Zia for valuable discussions. We thank R. F. L. Vermeulen and R. N. Schouten for assistance with the RF electronics, and M. Eschen for assistance with the experimental setup. We acknowledge support from the Netherlands Organisation for Scientific Research (NWO/OCW) through a Vidi grant, as part of the Frontiers of Nanoscience (NanoFront) programme and as part of the Quantum Software Consortium programme (project number 024.003.037/3368).
Author information
Authors and Affiliations
Contributions
M.H.A. and T.H.T. devised the experiments. M.H.A. performed the experiments. J.R. developed the 3D structure analysis method. M.H.A., J.R. and T.H.T. analysed the data. M.H.A., J.R., M.J.D. and C.E.B. prepared the experimental apparatus. C.E.B. and J.R. developed the RF electronics. H.P.B. and M.A.B. performed preliminary experiments. M.H.A., M.J.D., J.R., C.E.B. and T.H.T. developed the magnetic-field alignment procedure and the 14N echo spectroscopy. M.M. and D.J.T. grew the diamond sample. M.H.A., J.R. and T.H.T. wrote the manuscript with input from all authors. T.H.T. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature thanks Nir Bar-Gill, Vidya Praveen Bhallamudi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Experimental sequence.
The pulse sequence consists of five parts: sensor preparation, sensor initialization, polarization of the probe spin, double resonance, and detection of the probe spin. Sensor preparation: the NV centre is prepared by excitation with two 637-nm lasers for 150 μs and counting of the detected photons (read-out (RO) laser resonant with the Ex transition and initialization (Init) laser resonant with the E′ transition)24,34. If the number of photons exceeds a certain threshold, the NV is in the negative charge state and resonant with both lasers, and we proceed to the next step. If not, we apply a 515-nm laser (charge reset (RS) laser, 1 ms) and repeat the process24,34. Sensor initialization: the NV electron spin is initialized in the ms = 0 state through spin pumping (Init laser, 100 μs)34. Polarization of the probe spin: first, the NV sensor is brought into a superposition state using a π/2 pulse. Then, a dynamical decoupling sequence of N′ equally spaced π pulses of the form (τr − π − τr)N′ is applied to the electron spin. This sequence correlates the state of the nuclear spin(s) with the phase of the electron spin. We use two different sequences (see Methods). For sequence B, the microwave (MW) π pulses are interleaved with RF pulses (RF1) that resonantly drive the probe spin(s) (dashed box); see Bradley et al.28 for details. A second π/2 pulse maps the electron phase to the population and the electron spin is read out (RO laser). Double resonance: N echo pulses are applied simultaneously on the probe spin(s) (RF1) and the target spin(s) (RF2), so that the coupling between these spins is isolated. To mitigate pulse errors, we alternate the phases of the pulses following the XY8 scheme42. Detection of the probe spin: the detection sequence is the same as the polarization sequence except for the final RO laser pulse, which is applied for 10 μs and with higher power.
Extended Data Fig. 2 Ramsey experiments and reconstructed spectra.
a, Schematic of the pulse sequence used in the Ramsey experiment (equivalent to correlation spectroscopy); see Methods and Extended Data Fig. 1 for details. b, Ramsey signal for C2 and the corresponding PSD (5 kHz detuning). The red line represents the central frequency f0. Green lines are the 27 frequencies based on the seven strongest coupling strengths extracted from our high-resolution double-resonance spectroscopy (Supplementary Table 4). These frequencies are given by f0 ± f1 ± f2 ± f3 ± f4 ± f5 ± f6 ± f7, where f1 to f7 are the seven largest measured coupling strengths for C2. c–e, The same experiment for C3 (c; ~5 kHz detuning), C15 (d; ~1 kHz detuning) and C5 (e; ~2 kHz detuning).
Extended Data Fig. 3 Strongly coupled subclusters.
3D plots showing the structure of two strongly coupled subclusters (orange boxes) within the larger cluster (shown in the centre). Ramsey measurements performed on spins within these subclusters show clear beating signals within their dephasing time \({T}_{2}^{\ast }\) (see, for example, Extended Data Fig. 2). a, Eight-spin subcluster. b, Four-spin subcluster. Couplings above 3 Hz are marked blue, above 20 Hz green and above 50 Hz red. Grey points show the 2D projections of the diamond-lattice coordinates.
Extended Data Fig. 4 Finding the position of the NV centre.
a, 3D plot showing the 27-nuclear-spin cluster shown in Fig. 4, with the position of the nitrogen spin (green) and vacancy (purple) lattice sites calculated from the measured nitrogen–13C couplings. The grey dots show the 2D projections of the diamond-lattice coordinates. b, Bar plot showing the measured couplings fiN between 13C spin i and the nitrogen spin (grey), as well as the theoretically calculated couplings |CiN|/4π (green). Error bars are one standard deviation. See Supplementary Table 4 for the numerical values. c, Bar plots of Δr for the fitted position of the nitrogen spin (black) and fit errors δx (blue), δy (orange) and δz (green), where the 13C spins are fixed at the diamond-lattice solution. d, Plot of z versus \({r}_{xy}=\sqrt{{x}^{2}+{y}^{2}}\) for all lattice positions used in the DFT calculation from Nizovtsev et al.33 (blue) and for the appropriately transformed 13C coordinates found in this work (orange). Spins 5, 6, 9, 12 and 19 match a DFT lattice position, whereas the rest of the identified spins are outside the 510 lattice sites simulated. e, Measured electron–13C parallel (top) and perpendicular (bottom) hyperfine couplings for the five spins that are within the DFT calculation volume (red; from Supplementary Table 1), compared with the DFT results from ref. 33 (blue).
Extended Data Fig. 5 Aligning the magnetic field using a thermal echo sequence.
a, Pulse sequence used for the thermal echo measurement35. The electron spin is prepared in a superposition of the states ms = 0 and ms = −1 in the first half of the sequence and then swapped to a superposition of ms = 0 and ms = +1 for the second half, using a sequence of three closely spaced π pulses. By sweeping τ, the average frequency fTE = (f+1 + f−1)/2 is obtained, which is minimized when B⊥ = 0. f±1 are the ms = 0 ↔ ms = ±1 transition frequencies. The NV nitrogen spin is initialized in mI = 0 (ref. 34). b, Magnetic-field alignment by scanning the magnet position in two orthogonal directions. The obtained thermal echo frequencies are fitted with a parabolic function to find the optimum position (that is, minimal fTE). The plots show the frequency difference fTE − 2.877652 GHz. c, The magnet is placed at the optimum position and the measurement is repeated 200 times (over a 10-h period). The obtained average frequency difference is 0.13 kHz, with a standard deviation of 0.27 kHz, which is consistent with the statistical measurement error. Therefore, the total uncertainty for the magnet alignment is ~0.4 kHz, which corresponds to a perpendicular field of 0.5 G or a misalignment angle of 0.07°.
Supplementary information
Supplementary Information
This file contains additional details of the methods used in the paper, including supplementary discussion and derivations. In addition, it includes six supplementary figures and five supplementary tables, which summarize the experimental parameters used, nuclear spin properties, measured coupling strengths and obtained spatial coordinates of the spins in the cluster.
Rights and permissions
About this article
Cite this article
Abobeih, M.H., Randall, J., Bradley, C.E. et al. Atomic-scale imaging of a 27-nuclear-spin cluster using a quantum sensor. Nature 576, 411–415 (2019). https://doi.org/10.1038/s41586-019-1834-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1834-7
This article is cited by
-
Three-dimensional magnetic resonance tomography with sub-10 nanometer resolution
npj Quantum Information (2024)
-
Correlated sensing with a solid-state quantum multisensor system for atomic-scale structural analysis
Nature Photonics (2024)
-
Mapping a 50-spin-qubit network through correlated sensing
Nature Communications (2024)
-
Quantum sensors for biomedical applications
Nature Reviews Physics (2023)
-
Quantum microscopy with van der Waals heterostructures
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.