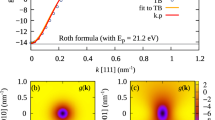
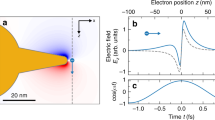
Abstract
The macroscopic electromagnetic boundary conditions, which have been established for over a century1, are essential for the understanding of photonics at macroscopic length scales. Even state-of-the-art nanoplasmonic studies2,3,4, exemplars of extremely interface-localized fields, rely on their validity. This classical description, however, neglects the intrinsic electronic length scales (of the order of ångström) associated with interfaces, leading to considerable discrepancies between classical predictions and experimental observations in systems with deeply nanoscale feature sizes, which are typically evident below about 10 to 20 nanometres5,6,7,8,9,10. The onset of these discrepancies has a mesoscopic character: it lies between the granular microscopic (electronic-scale) and continuous macroscopic (wavelength-scale) domains. Existing top-down phenomenological approaches deal only with individual aspects of these omissions, such as nonlocality11,12,13 and local-response spill-out14,15. Alternatively, bottom-up first-principles approaches—for example, time-dependent density functional theory16,17—are severely constrained by computational demands and thus become impractical for multiscale problems. Consequently, a general and unified framework for nanoscale electromagnetism remains absent. Here we introduce and experimentally demonstrate such a framework—amenable to both analytics and numerics, and applicable to multiscale problems—that reintroduces the electronic length scale via surface-response functions known as Feibelman d parameters18,19. We establish an experimental procedure to measure these complex dispersive surface-response functions, using quasi-normal-mode perturbation theory and observations of pronounced nonclassical effects. We observe nonclassical spectral shifts in excess of 30 per cent and the breakdown of Kreibig-like broadening in a quintessential multiscale architecture: film-coupled nanoresonators, with feature sizes comparable to both the wavelength and the electronic length scale. Our results provide a general framework for modelling and understanding nanoscale (that is, all relevant length scales above about 1 nanometre) electromagnetic phenomena.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Maxwell, J. C. A dynamical theory of the electromagnetic field. Philos. Trans. R. Soc. Lond. 155, 459–512 (1865).
Nielsen, M., Shi, X., Dichtl, P., Maier, S. A. & Oulton, R. F. Giant nonlinear response at a plasmonic nanofocus drives efficient four-wave mixing. Science 358, 1179–1181 (2017).
Chikkaraddy, R. et al. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 535, 127–130 (2016).
Akselrod, G. M. et al. Probing the mechanisms of large Purcell enhancement in plasmonic nanoantennas. Nat. Photon. 8, 835–840 (2014).
Kreibig, U. & Genzel, L. Optical absorption of small metallic particles. Surf. Sci. 156, 678–700 (1985).
Tiggesbäumker, J., Köller, L., Meiwes-Broer, K.-H. & Liebsch, A. Blue shift of the Mie plasma frequency in Ag clusters and particles. Phys. Rev. A 48, R1749–R1752 (1993).
Cottancin, E. et al. Optical properties of noble metal clusters as a function of the size: comparison between experiments and a semi-quantal theory. Theor. Chem. Acc. 116, 514–523 (2006).
Ciracì, C. et al. Probing the ultimate limits of plasmonic enhancement. Science 337, 1072–1074 (2012).
Scholl, J. A., Koh, A. L. & Dionne, J. A. Quantum plasmon resonances of individual metallic nanoparticles. Nature 483, 421–427 (2012).
Raza, S. et al. Blueshift of the surface plasmon resonance in silver nanoparticles studied with EELS. Nanophotonics 2, 131–138 (2013).
Boardman, A. D. Electromagnetic Surface Modes (John Wiley & Sons, 1982).
Fernández-Domínguez, A. I., Wiener, A., García-Vidal, F. J., Maier, S. A. & Pendry, J. B. Transformation-optics description of nonlocal effects in plasmonic nanostructures. Phys. Rev. Lett. 108, 106802 (2012).
Raza, S., Bozhevolnyi, S. I., Wubs, M. & Mortensen, N. A. Nonlocal optical response in metallic nanostructures. J. Phys. Condens. Matter 27, 183204 (2015).
Zhu, W. et al. Quantum mechanical effects in plasmonic structures with subnanometre gaps. Nat. Commun. 7, 11495 (2016).
Skjølstrup, E. J. H., Søndergaard, T. & Pedersen, T. G. Quantum spill-out in few-nanometer metal gaps: effect on gap plasmons and reflectance from ultrasharp groove arrays. Phys. Rev. B 97, 115429 (2018).
Zuloaga, J., Prodan, E. & Nordlander, P. Quantum description of the plasmon resonances of a nanoparticle dimer. Nano Lett. 9, 887–891 (2009).
Teperik, T. V., Nordlander, P., Aizpurua, J. & Borisov, A. G. Robust subnanometric plasmon ruler by rescaling of the nonlocal optical response. Phys. Rev. Lett. 110, 263901 (2013).
Feibelman, P. J. Surface electromagnetic fields. Prog. Surf. Sci. 12, 287–407 (1982).
Liebsch, A. Electronic Excitations at Metal Surfaces (Springer, 1997).
Halperin, W. P. Quantum size effects in metal particles. Rev. Mod. Phys. 58, 533–606 (1986).
Yan, W., Wubs, M. & Mortensen, N. A. Projected dipole model for quantum plasmonics. Phys. Rev. Lett. 115, 137403 (2015).
Christensen, T., Yan, W., Jauho, A.-P., Soljačić, M. & Mortensen, N. A. Quantum corrections in nanoplasmonics: shape, scale, and material. Phys. Rev. Lett. 118, 157402 (2017).
Apell, P. & Ljungbert, A. A general non-local theory for the electromagnetic response of a small metal particle. Phys. Scr. 26, 113–118 (1982).
Liebsch, A. Dynamical screening at simple-metal surfaces. Phys. Rev. B 36, 7378–7388 (1987).
Liebsch, A. Surface-plasmon dispersion and size dependence of Mie resonance: silver versus simple metals. Phys. Rev. B 48, 11317–11328 (1993).
Feibelman, P. J. Comment on “Surface plasmon dispersion of Ag”. Phys. Rev. Lett. 72, 788 (1994).
Lalanne, P., Yan, W., Vynck, K., Sauvan, C. & Hugonin, J.-P. Light interaction with photonic and plasmonic resonances. Laser Photonics Rev. 12, 1700113 (2018).
Yan, W., Faggiani, R. & Lalanne, P. Rigorous modal analysis of plasmonic nanoresonators. Phys. Rev. B 97, 205422 (2018).
Yang, Y., Miller, O. D., Christensen, T., Joannopoulos, J. D. & Soljačić, M. Low-loss plasmonic dielectric nanoresonators. Nano Lett. 17, 3238–3245 (2017).
Yang, J., Giessen, H. & Lalanne, P. Simple analytical expression for the peak-frequency shifts of plasmonic resonances for sensing. Nano Lett. 15, 3439–3444 (2015).
Jin, D. et al. Quantum-spillover-enhanced surface-plasmonic absorption at the interface of silver and high-index dielectrics. Phys. Rev. Lett. 115, 193901 (2015).
Groner, M. D., Elam, J. W., Fabreguette, F. H. & George, S. M. Electrical characterization of thin Al2O3 films grown by atomic layer deposition on silicon and various metal substrates. Thin Solid Films 413, 186–197 (2002).
Banerjee, A. et al. Optical properties of refractory metal based thin films. Opt. Mater. Express 8, 2072–2088 (2018).
Acknowledgements
We thank J. Daley, S. E. Kooi and M. Mondol for assistance in sample fabrication and measurement. We thank F. Niroui and T. Zhu for lending us equipment. We acknowledge discussions with V. Bulović, O. D. Miller and N. A. Mortensen. We thank P. Rebusco for reading and editing the manuscript. K.K.B. thanks A. Chu and J. Wanapun for support. This work was partly supported by the US Army Research Office through the Institute for Soldier Nanotechnologies under contract number W911NF-18-2-0048 and W911NF-13-D-0001, and by Air Force Office of Scientific Research (AFOSR) under grant contract number FA9550-18-1-0436. Y.Y. was partly supported by the MRSEC Program of the National Science Foundation under grant number DMR-1419807. D.Z. was supported by a National Science Scholarship from A*STAR, Singapore. W.Y. was supported by Programme IdEx Bordeaux-LAPHIA (grant number ANR-10- IDEX-03-02) and project ‘Resonance’ (grant number ANR-16-CE24-0013) of the French National Agency for Research (ANR). M.Z. was supported by the National Natural Science Foundation of China (grant number 11574078) and the China Scholarship Council. T.C. was supported by the Danish Council for Independent Research (grant number DFFC6108-00667).
Author information
Authors and Affiliations
Contributions
Y.Y. and T.C. conceived the idea. D.Z. fabricated the samples. Y.Y. and D.Z. designed the experiment, built the setup, conducted the scattering measurements and performed the ellipsometry. T.C. derived the mesoscopic boundary conditions. Y.Y., W.Y. and T.C. developed the numerical methods and Y.Y. performed the numerical calculations. W.Y. proposed the auxiliary-potential method, performed density functional theory calculations and implemented the QNM-based perturbation analysis. D.Z. performed the atomic-force microscopy measurement. A.A. and D.Z. performed the transmission electron microscopy measurement. D.Z. and M.Z. characterized nanoparticle size statistics. Y.Y., D.Z., W.Y. and T.C. analysed the data. Y.Y., D.Z. and T.C. drafted the manuscript with extensive input from all authors. J.D.J., P.L., T.C., K.K.B. and M.S. supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Michal Lipson and Javier Aizpurua for their contribution to the peer review of this work.
Supplementary information
Supplementary Information
This file contains supplementary text sections S1–S16, which includes supplementary figures and tables.
Rights and permissions
About this article
Cite this article
Yang, Y., Zhu, D., Yan, W. et al. A general theoretical and experimental framework for nanoscale electromagnetism. Nature 576, 248–252 (2019). https://doi.org/10.1038/s41586-019-1803-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1803-1
This article is cited by
-
Ultrasmall and tunable TeraHertz surface plasmon cavities at the ultimate plasmonic limit
Nature Communications (2023)
-
Electromagnetic Response of Core-Satellite Nanoparticles for Application in Photothermal Conversion
Plasmonics (2023)
-
Surface Dyakonov–Cherenkov radiation
eLight (2022)
-
Extremely confined gap plasmon modes: when nonlocality matters
Nature Communications (2022)
-
An image interaction approach to quantum-phase engineering of two-dimensional materials
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.