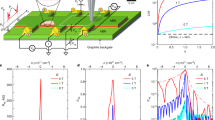
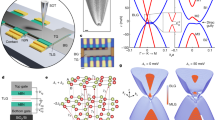
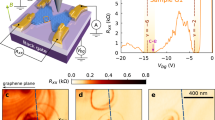
Abstract
Topology is a powerful recent concept asserting that quantum states could be globally protected against local perturbations1,2. Dissipationless topologically protected states are therefore of major fundamental interest as well as of practical importance in metrology and quantum information technology. Although topological protection can be robust theoretically, in realistic devices it is often susceptible to various dissipative mechanisms, which are difficult to study directly because of their microscopic origins. Here we use scanning nanothermometry3 to visualize and investigate the microscopic mechanisms that undermine dissipationless transport in the quantum Hall state in graphene. Simultaneous nanoscale thermal and scanning gate microscopy shows that the dissipation is governed by crosstalk between counterpropagating pairs of downstream and upstream channels that appear at graphene boundaries as a result of edge reconstruction. Instead of local Joule heating, however, the dissipation mechanism comprises two distinct and spatially separated processes. The work-generating process that we image directly, which involves elastic tunnelling of charge carriers between the quantum channels, determines the transport properties but does not generate local heat. By contrast, the heat and entropy generation process—which we visualize independently—occurs nonlocally upon resonant inelastic scattering from single atomic defects at graphene edges, and does not affect transport. Our findings provide an insight into the mechanisms that conceal the true topological protection, and suggest routes towards engineering more robust quantum states for device applications.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Data supporting the findings of this study are available within the article and its Supplementary Information files and from the corresponding authors upon reasonable request.
Change history
27 November 2019
An Amendment to this paper has been published and can be accessed via a link at the top of the paper.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Halbertal, D. et al. Nanoscale thermal imaging of dissipation in quantum systems. Nature 539, 407–410 (2016).
Tzalenchuk, A. et al. Towards a quantum resistance standard based on epitaxial graphene. Nat. Nanotechnol. 5, 186–189 (2010).
Weis, J. & von Klitzing, K. Metrology and microscopic picture of the integer quantum Hall effect. Philos. Trans. R. Soc. A 369, 3954–3974 (2011).
Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 38, 9375–9389 (1988).
Silvestrov, P. G. & Efetov, K. B. Charge accumulation at the boundaries of a graphene strip induced by a gate voltage: Electrostatic approach. Phys. Rev. B 77, 155436 (2008).
Cui, Y.-T. et al. Unconventional correlation between quantum Hall transport quantization and bulk state filling in gated graphene devices. Phys. Rev. Lett. 117, 186601 (2016).
Vasyukov, D. et al. A scanning superconducting quantum interference device with single electron spin sensitivity. Nat. Nanotechnol. 8, 639–644 (2013).
Eriksson, M. A. et al. Cryogenic scanning probe characterization of semiconductor nanostructures. Appl. Phys. Lett. 69, 671–673 (1996).
Halbertal, D. et al. Imaging resonant dissipation from individual atomic defects in graphene. Science 358, 1303–1306 (2017).
Altimiras, C. et al. Tuning energy relaxation along quantum Hall channels. Phys. Rev. Lett. 105, 226804 (2010).
Venkatachalam, V., Hart, S., Pfeiffer, L., West, K. & Yacoby, A. Local thermometry of neutral modes on the quantum Hall edge. Nat. Phys. 8, 676–681 (2012).
Itoh, K. et al. Signatures of a nonthermal metastable state in copropagating quantum Hall edge channels. Phys. Rev. Lett. 120, 197701 (2018).
Tikhonov, K. S., Gornyi, I. V., Kachorovskii, V. Y. & Mirlin, A. D. Resonant supercollisions and electron-phonon heat transfer in graphene. Phys. Rev. B 97, 085415 (2018).
Kong, J. F., Levitov, L., Halbertal, D. & Zeldov, E. Resonant electron-lattice cooling in graphene. Phys. Rev. B 97, 245416 (2018).
Chae, J. et al. Enhanced carrier transport along edges of graphene devices. Nano Lett. 12, 1839 (2012).
Panchal, V. et al. Visualisation of edge effects in side-gated graphene nanodevices. Sci. Rep. 4, 5881 (2014).
Vera-Marun, I. J. et al. Quantum Hall transport as a probe of capacitance profile at graphene edges. Appl. Phys. Lett. 102, 013106 (2013).
Barraud, C. et al. Field effect in the quantum Hall regime of a high mobility graphene wire. J. Appl. Phys. 116, 073705 (2014).
Akiho, T., Irie, H., Onomitsu, K. & Muraki, K. Counterflowing edge current and its equilibration in quantum Hall devices with sharp edge potential: Roles of incompressible strips and contact configuration. Phys. Rev. B 99, 121303 (2019).
Ma, E. Y. et al. Unexpected edge conduction in mercury telluride quantum wells under broken time-reversal symmetry. Nat. Commun. 6, 7252 (2015).
Shtanko, O. & Levitov, L. Robustness and universality of surface states in Dirac materials. Proc. Natl Acad. Sci. USA 115, 5908–5913 (2018).
Akhmerov, A. R. & Beenakker, C. W. J. Boundary conditions for Dirac fermions on a terminated honeycomb lattice. Phys. Rev. B 77, 085423 (2008).
Allen, M. T. et al. Spatially resolved edge currents and guided-wave electronic states in graphene. Nat. Phys. 12, 128–133 (2016).
Amet, F. et al. Supercurrent in the quantum Hall regime. Science 352, 966–969 (2016).
Zhu, M. J. et al. Edge currents shunt the insulating bulk in gapped graphene. Nat. Commun. 8, 14552 (2017).
Indolese, D. I. et al. Signatures of van Hove singularities probed by the supercurrent in a graphene–hBN superlattice. Phys. Rev. Lett. 121, 137701 (2018).
Pribiag, V. S. et al. Edge-mode superconductivity in a two-dimensional topological insulator. Nat. Nanotechnol. 10, 593–597 (2015).
Lee, G.-H. et al. Inducing superconducting correlation in quantum Hall edge states. Nat. Phys. 13, 693–698 (2017).
de Vries, F. K. et al. h/e Superconducting quantum interference through trivial edge states in InAs. Phys. Rev. Lett. 120, 047702 (2018).
Ribeiro-Palau, R. et al. High-quality electrostatically defined Hall bars in monolayer graphene. Nano Lett. 19, 2583–2587 (2019).
Pizzocchero, F. et al. The hot pick-up technique for batch assembly of van der Waals heterostructures. Nat. Commun. 7, 11894 (2016).
Ella, L. et al. Simultaneous voltage and current density imaging of flowing electrons in two dimensions. Nat. Nanotechnol. 14, 480–487 (2019).
Finkler, A. et al. Self-aligned nanoscale SQUID on a tip. Nano Lett. 10, 1046–1049 (2010).
Finkler, A. et al. Scanning superconducting quantum interference device on a tip for magnetic imaging of nanoscale phenomena. Rev. Sci. Instrum. 83, 073702 (2012).
Paradiso, N. et al. Spatially resolved analysis of edge-channel equilibration in quantum Hall circuits. Phys. Rev. B 83, 155305 (2011).
Garcia, A. G. F., König, M., Goldhaber-Gordon, D. & Todd, K. Scanning gate microscopy of localized states in wide graphene constrictions. Phys. Rev. B 87, 085446 (2013).
Pascher, N. et al. Imaging the conductance of integer and fractional quantum Hall edge states. Phys. Rev. X 4, 011014 (2014).
Bhandari, S. et al. Imaging cyclotron orbits of electrons in graphene. Nano Lett. 16, 1690–1694 (2016).
Braem, B. A. et al. Investigating energy scales of fractional quantum Hall states using scanning gate microscopy. Phys. Rev. B 93, 115442 (2016).
Dou, Z. et al. Imaging bulk and edge transport near the Dirac point in graphene moiré superlattices. Nano Lett. 18, 2530–2537 (2018).
Herbschleb, E. D. et al. Direct imaging of coherent quantum transport in graphene p–n–p junctions. Phys. Rev. B 92, 125414 (2015).
Schnez, S. et al. Imaging localized states in graphene nanostructures. Phys. Rev. B 82, 165445 (2010).
Bischoff, D. et al. Localized charge carriers in graphene nanodevices. Appl. Phys. Rev. 2, 031301 (2015).
Vasko, F. T. & Zozoulenko, I. V. Conductivity of a graphene strip: width and gate-voltage dependencies. Appl. Phys. Lett. 97, 092115 (2010).
Woessner, A. et al. Near-field photocurrent nanoscopy on bare and encapsulated graphene. Nat. Commun. 7, 10783 (2016).
Acknowledgements
We thank G. Zhang, I. V. Gornyi, A. D. Mirlin and Y. Gefen for discussions and theoretical analysis, M. E. Huber for SOT readout setup, and M. L. Rappaport for technical assistance. This work was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant number 785971), by the Israel Science Foundation (ISF; grant number 921/18), by the Minerva Foundation with funding from the Federal German Ministry of Education and Research, by the German-Israeli Foundation (GIF), by the Weizmann–UK Making Connections Program, and by Manchester Graphene-NOWNANO CDT EP/L-1548X. E.Z. acknowledges the support of the Leona M. and Harry B. Helmsley Charitable Trust grant 2018PG-ISL006.
Author information
Authors and Affiliations
Contributions
A.M., A.A.-S., D.H., I.M. and E.Z. conceived the experiments. J.B. and D.J.P. conceived and fabricated the samples. A.M. and A.A.-S. carried out the measurements and data analysis. D.H. and I.M. performed preliminary studies. K.B. and Y.M. fabricated the SOTs and the tuning fork feedback. A.M., E.Z., A.A.-S., D.J.P., J.B. and A.K.G. wrote the manuscript. All authors participated in discussions and writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Xi Lin and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Optical image of sample A.
Shown are the hBN/graphene/hBN heterostructure (green), the etched regions exposing the SiO2/Si substrate (dark) and the metal contacts (yellow). The dashed rectangles mark the regions shown in Fig. 2 (red) and Supplementary Video 2 (blue). The current is applied to the bottom constriction and drained at the top contact, and the corresponding voltages Vxx and V2p are measured in the scanning-gate mode. The dashed line on the right shows the native edge of graphene encapsulated in hBN.
Extended Data Fig. 2 Optical and scanning electron microscopy images of sample B.
a, Optical image showing the hBN/graphene/hBN heterostructure (light green), etched tranches exposing the SiO2/Si substrate (light blue), bottom plunger gates (light brown) and the metal contacts (dark). The dashed rectangle marks the region shown in Fig. 3, Extended Data Figs. 6, 7, 9, Supplementary Fig. 2 and with variable voltage Vpg applied to the plunger gates. The current is applied to the top contact and drained at the bottom contact and the corresponding voltages Vxx and V2p are measured in the scanning gate mode. b, Scanning electron micrograph of a twin sample of device B showing (from bright to dark) the metal contacts, four plunger gates, hBN/graphene/hBN, and the etched trenches.
Extended Data Fig. 3 Optical image of sample C.
Shown are the hBN/graphene/hBN heterostructure (light brown), etched trenches exposing the SiO2/Si substrate (light cyan) and the metal contacts (yellow). The bottom plunger gates are difficult to distinguish in the optical image and are artificially highlighted in a dark orange colour. The dashed rectangle marks the region shown in Supplementary Fig. 2. The current is applied to the top contact and drained at the bottom, and the corresponding voltages Vxx and V2p are measured in the scanning gate mode.
Extended Data Fig. 4 Transport measurements of samples B and C.
a, b, Colour rendering of Rxx of samples B (a) and C (b) as a function of the back-gate voltage Vbg and the applied perpendicular magnetic field Bz.
Extended Data Fig. 5 Effect of the plunger gate on transport characteristics.
a, An optical image of device B with the measurement circuit shown. b, Four-probe measurements of Hall conductance \({\sigma }_{yx}={R}_{yx}/({R}_{xx}^{2}+{R}_{yx}^{2})\) and Rxx against back-gate voltage Vbg for different Vpg values at Bz = 0.9 T and Iac = 50 nA at 93.72 Hz. A voltage of 3 V was applied to the two plunger gates on the right edge and \(-\)3 V was applied to the top plunger gate on the left edge. In this configuration the nontopological quantum Hall channels on the right edge of the sample are cut off, giving rise to enhanced \({R}_{xx}\) response on the left edge upon varying Vpg. c, Rxx plotted against Vbg from b plotted on a logarithmic scale. d, Values from the four-probe measurement of Rxx plotted against Vpg at Vbg = −1 V (dashed line in c).
Extended Data Fig. 6 Visualization of bulk current flow upon cutting off nontopological channels.
a, Schematic trajectories of quantum Hall edge channels with the nontopological pair of channels cut off by the hole-depleting plunger gate. b, Scanning gate Rxx(r) image in sample B at Vbg = −1.2 V, Vtg = 3 V, Vpg = −0.1 V and Idc = 1.75 µA, revealing current flowing through the bulk the in the cut-off region (diffuse red blob). c, Tac(r) acquired simultaneously with Rxx(r) showing \(\dot{Q}\) rings along the graphene boundaries due to nonlocal dissipation. The images were acquired in the dashed red area in Extended Data Fig. 2.
Extended Data Fig. 7 Demonstration of hole edge accumulation in n-doped bulk.
a, Scanning gate Rxx(r) imaging of sample B (in the red dashed area in Extended Data Fig. 2) in the vicinity of n-doped ν = 2 plateau (Vbg = 0.12 V, ν = 2.07, Vpg = −2 V, see Extended Data Fig. 5c for transport) using a positive Vtg of 6 V. The depletion of the hole accumulated edges by the positive Vtg cases increase in Rxx(r) similar to the case of the p-doped bulk. b, Same as a in the vicinity of the ν = 6 plateau (Vbg = 1.475 V, ν = 5.98). In both images, Idc = 1.75 µA.
Extended Data Fig. 8 Effect of the tip potential Vtg on the quantum Hall channels with p-doped edge accumulation.
a–d, Schematic trajectories of the edge channels upon increasing Vtg. a, Non-perturbing tip at flat band conditions \({V}_{{\rm{tg}}}={V}_{{\rm{tg}}}^{{\rm{FB}}}\approx 0{\rm{V}}\). b, Application of a weakly perturbing Vtg slightly reduces the edge hole accumulation and shifts the nontopological quantum Hall channels closer to each other. c, A stronger depleting Vtg cuts off the nontopological pair of channels. d, A higher Vtg forms an n-doped region under the tip.
Extended Data Fig. 9 Demonstration of elastic tunnelling by comparing perturbing and non-perturbing tip potential in sample B.
a, Two probe R2p(r) in the case of non-perturbing \({V}_{{\rm{tg}}}=0.05{\rm{V}}\approx {V}_{{\rm{tg}}}^{{\rm{FB}}}\) showing essentially constant R2p(r). b, The corresponding Tdc(r) shows the current-induced temperature variation in the sample unperturbed by the tip at Vbg = −1.1 V (ν = −1.44), Vpg = −2 V and Idc = 1.75 µA. The increased temperature at the bottom-right corner is caused by heat diffusion from the hot spot at the nearby current contact. c, R2p(r) for Vtg = 3 V revealing the location of \(\dot{W}({\bf{r}})\) processes by perturbing the local work by \(\delta \dot{W}({\bf{r}})\) through enhanced backscattering. d, The corresponding Tdc(r) showing the temperature map mimicking the R2p(r) signal caused by the enhanced nonlocal heat release \(\dot{Q}\) due to tip-induced \(\delta \dot{W}({\bf{r}})\). e, Horizontal line cuts of Tdc(r) along the green and blue lines in b. The green data show a peak at the graphene boundary (dashed yellow line in b) followed by a slowly decaying tail into the bulk, whereas the blue data display no peak at the inner edge of the plunger gates, showing that the \(\dot{W}({\bf{r}})\) process there is elastic. f, Vertical line cut through the protrusion region showing peaks at the graphene boundaries with overlapping tails in the middle. The coloured dots are the intersection points of the lines.
Supplementary information
Supplementary Information
This provides additional discussion about supplementary scans and supplementary videos supporting the claims of the presented paper. It contains extensive discussion of the five Supplementary Videos and of Supplementary Figs. S1 to S3. Supplementary Fig. S1 supports the discussion of Supplementary Video V2 and Supplementary Figs. S2 and S3 demonstrate additional examples of plunger gate modification of edge reconstruction.
Supplementary Video 1
Thermal imaging \({T}_{ac}(r)\) vs \({V}_{bg}\) of sample A. Full sequence of \({T}_{ac}({\boldsymbol{r}})\) scans shown in Fig. 1c,d for backgate voltages \({V}_{bg}\) incremented from \(-\)8 V to 8 V at \(T=\) 4.2 K, \({B}_{z}=\) 1 T, and \({V}_{tg}=\) 8 V
Supplementary Video 2
Scanning gate imaging \({R}_{xx}(r)\) vs \({V}_{bg}\) of sample A. A sequence of scanning gate images of the four-probe resistance \({R}_{xx}({\boldsymbol{r}})\) in a zoomed-in region along the top boundary of sample A. The \({R}_{xx}({\boldsymbol{r}})={V}_{xx}({\boldsymbol{r}})/{I}_{dc}\) is recorded as a function of the tip position \({\boldsymbol{r}}\) for a range of back gate voltages \({V}_{bg}\) from \(-\)6 V to \(-\)1.9 V (\(\nu \,\)from \(-\)10.7 to 0.09) in small steps of \( \sim \)30 mV. Here \({B}_{z}=\) 1.0 T, \({V}_{tg}=\) 1 V, and the value of the applied current \({I}_{dc}\) is adjusted for each \({V}_{bg}\) to maintain total power dissipated in the sample of \({R}_{2p}{I}_{dc}^{2}=\) 2 nW. The dashed horizontal line denotes the top edge of the sample
Supplementary Video 3
Plunger gate \({V}_{pg}\) dependence. An example of the evolution of the simultaneously acquired thermal \({T}_{ac}({\boldsymbol{r}})\) and scanning gate \({R}_{xx}({\boldsymbol{r}})\) images in sample B upon varying \({V}_{pg}\) from +0.6 V to -2.0 V similarly to Fig. 3 for \({V}_{bg}=-\)1.05 V, \({V}_{tg}=\) 6 V, and \({I}_{dc}=\) 1.75 µA. At this higher \({V}_{tg}\) the \(\dot{Q}\) rings and the \(\dot{W}\) arc-like features are readily resolved. The \(\dot{Q}\) rings due to phonon emission at the atomic defects are observed in the \({T}_{ac}({\boldsymbol{r}})\) images along the entire graphene perimeter, visible in the form of smaller diameter sharp rings
Supplementary Video 4
Current dependence. A sequence of \({R}_{xx}({\boldsymbol{r}})\) in sample B as a function of applied current \({I}_{ac}\), from 10 nA to 1.4 \(\mu \)A, at \({V}_{bg}=-\)1.0 V, \({V}_{pg}=-\)2.0 V, and \({V}_{tg}=\) 8.0 V
Supplementary Video 5
Effects of tip potential \({V}_{tg}\) on \({R}_{xx}(r)\). An example of the evolution of \({R}_{xx}({\boldsymbol{r}})\) upon varying \({V}_{tg}\) from -2 V to +10.25 V in sample B, at \({V}_{bg}=-\)1 V (\(\nu =-\)1.15), \({V}_{pg}=-\)0.22 V (neutral plunger gate), and very low current of \({I}_{ac}=\) 10 nA
Rights and permissions
About this article
Cite this article
Marguerite, A., Birkbeck, J., Aharon-Steinberg, A. et al. Imaging work and dissipation in the quantum Hall state in graphene. Nature 575, 628–633 (2019). https://doi.org/10.1038/s41586-019-1704-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1704-3
This article is cited by
-
Demonstration and imaging of cryogenic magneto-thermoelectric cooling in a van der Waals semimetal
Nature Physics (2024)
-
Beryllene, the lightest Xene
npj 2D Materials and Applications (2023)
-
Para-hydrodynamics from weak surface scattering in ultraclean thin flakes
Nature Communications (2023)
-
Direct visualization of electronic transport in a quantum anomalous Hall insulator
Nature Materials (2023)
-
Transport measurement of fractional charges in topological models
npj Quantum Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.