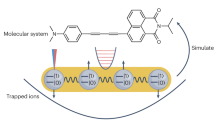
Abstract
Computing the electronic structure of molecules with high precision is a central challenge in the field of quantum chemistry. Despite the success of approximate methods, tackling this problem exactly with conventional computers remains a formidable task. Several theoretical1,2 and experimental3,4,5 attempts have been made to use quantum computers to solve chemistry problems, with early proof-of-principle realizations done digitally. An appealing alternative to the digital approach is analogue quantum simulation, which does not require a scalable quantum computer and has already been successfully applied to solve condensed matter physics problems6,7,8. However, not all available or planned setups can be used for quantum chemistry problems, because it is not known how to engineer the required Coulomb interactions between them. Here we present an analogue approach to the simulation of quantum chemistry problems that relies on the careful combination of two technologies: ultracold atoms in optical lattices and cavity quantum electrodynamics. In the proposed simulator, fermionic atoms hopping in an optical potential play the role of electrons, additional optical potentials provide the nuclear attraction, and a single-spin excitation in a Mott insulator mediates the electronic Coulomb repulsion with the help of a cavity mode. We determine the operational conditions of the simulator and test it using a simple molecule. Our work opens up the possibility of efficiently computing the electronic structures of molecules with analogue quantum simulation.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Code and data availability
The computer code developed for this study is available from the corresponding authors upon reasonable request. All data supporting the findings of this study can be generated using the numerical methods described within Methods and Supplementary Information and are available upon reasonable request.
References
Aspuru-Guzik, A., Dutoi, A. D., Love, P. J. & Head-Gordon, M. Simulated quantum computation of molecular energies. Science 309, 1704–1707 (2005).
Wecker, D., Bauer, B., Clark, B. K., Hastings, M. B. & Troyer, M. Gate-count estimates for performing quantum chemistry on small quantum computers. Phys. Rev. A 90, 022305 (2014).
O’Malley, P. et al. Scalable quantum simulation of molecular energies. Phys. Rev. X 6, 031007 (2016).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Lanyon, B. P. et al. Towards quantum chemistry on a quantum computer. Nat. Chem. 2, 106–111 (2010).
Choi, J.-y. et al. Exploring the many-body localization transition in two dimensions. Science 352, 1547–1552 (2016).
Trotzky, S. et al. Probing the relaxation towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. Nat. Phys. 8, 325–330 (2012).
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2002).
Feynman, R. P. Simulating physics with computers. Int. J. Theor. Phys. 217, 467–488 (1982).
Cao, Y. et al. Quantum chemistry in the age of quantum computing. Chem. Rev. https://doi.org/10.1021/acs.chemrev.8b00803 (2019).
Kassal, I., Whitfield, J. D., Perdomo-Ortiz, A., Yung, M.-H. & Aspuru-Guzik, A. Simulating chemistry using quantum computers. Annu. Rev. Phys. Chem. 62, 185–207 (2011).
Reiher, M., Wiebe, N., Svore, K. M., Wecker, D. & Troyer, M. Elucidating reaction mechanisms on quantum computers. Proc. Natl Acad. Sci. USA 114, 7555–7560 (2017).
Cirac, J. I. & Zoller, P. Goals and opportunities in quantum simulation. Nat. Phys. 8, 264–266 (2012).
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008).
Murch, K. W., Moore, K. L., Gupta, S. & Stamper-Kurn, D. M. Observation of quantum-measurement backaction with an ultracold atomic gas. Nat. Phys. 4, 561–564 (2008).
Krinner, L., Stewart, M., Pazmiño, A., Kwon, J. & Schneble, D. Spontaneous emission of matter waves from a tunable open quantum system. Nature 559, 589–592 (2018).
Ritsch, H., Domokos, P., Brennecke, F. & Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 85, 553–601 (2013).
Schreppler, S. et al. Optically measuring force near the standard quantum limit. Science 344, 1486–1489 (2014).
Brennecke, F., Ritter, S., Donner, T. & Esslinger, T. Cavity optomechanics with a Bose–Einstein condensate. Science 322, 235–238 (2008).
Brennecke, F. et al. Cavity QED with a Bose–Einstein condensate. Nature 450, 268–271 (2007).
Domokos, P. & Ritsch, H. Collective cooling and self-organization of atoms in a cavity. Phys. Rev. Lett. 89, 253003 (2002).
Szabo, A. & Ostlund, N. S. Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory (Courier Corporation, 2012).
Daley, A. J., Boyd, M. M., Ye, J. & Zoller, P. Quantum computing with alkaline-earth-metal atoms. Phys. Rev. Lett. 101, 170504 (2008).
Sturm, M. R., Schlosser, M., Walser, R. & Birkl, G. Quantum simulators by design: many-body physics in reconfigurable arrays of tunnel-coupled traps. Phys. Rev. A 95, 063625 (2017).
Barredo, D., Lienhard, V., de Léséleuc, S., Lahaye, T. & Browaeys, A. Synthetic three-dimensional atomic structures assembled atom by atom. Nature 561, 79–82 (2018).
Riegger, L. et al. Localized magnetic moments with tunable spin exchange in a gas of ultracold fermions. Phys. Rev. Lett. 120, 143601 (2018).
de Vega, I., Porras, D. & Cirac, J. I. Matter-wave emission in optical lattices: single particle and collective effects. Phys. Rev. Lett. 101, 260404 (2008).
Kołos, W. & Wolniewicz, L. Accurate adiabatic treatment of the ground state of the hydrogen molecule. J. Chem. Phys. 41, 3663–3673 (1964).
Sims, J. S. & Hagstrom, S. A. High precision variational calculations for the Born–Oppenheimer energies of the ground state of the hydrogen molecule. J. Chem. Phys. 124, 094101 (2006).
Gerchberg, R. & Saxton, O. A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 35, 237–246 (1971).
Whyte, G. & Courtial, J. Experimental demonstration of holographic three-dimensional light shaping using a Gerchberg–Saxton algorithm. New J. Phys. 7, 117 (2005).
Soifer, V. A., Kotlar, V. & Doskolovich, L. Iteractive Methods for Diffractive Optical Elements Computation (CRC Press, 2014).
Ye, J., Kimble, H. & Katori, H. Quantum state engineering and precision metrology using state-insensitive light traps. Science 320, 1734–1738 (2008).
Crubellier, A., González-Férez, R., Koch, C. P. & Luc-Koenig, E. Controlling the s-wave scattering length with nonresonant light: predictions of an asymptotic model. Phys. Rev. A 95, 023405 (2017).
Mandel, O. et al. Coherent transport of neutral atoms in spin-dependent optical lattice potentials. Phys. Rev. Lett. 91, 010407 (2003).
Anderlini, M., Sebby-Strabley, J., Kruse, J., Porto, J. V. & Phillips, W. D. Controlled atom dynamics in a double-well optical lattice. J. Phys. B 39, S199–S210 (2006).
Parr, R. G. & Yang, W. Density-Functional Theory of Atoms and Molecules (Oxford Univ. Press, 1989).
Omran, A. et al. Microscopic observation of Pauli blocking in degenerate fermionic lattice gases. Phys. Rev. Lett. 115, 263001 (2015).
Gupta, V. P. Principles and Applications of Quantum Chemistry (Academic Press, 2015).
Schleier-Smith, M. H., Leroux, I. D., Zhang, H., Van Camp, M. A. & Vuletić, V. Optomechanical cavity cooling of an atomic ensemble. Phys. Rev. Lett. 107, 143005 (2011).
Acknowledgements
We thank S. Blatt and N. Meyer for useful discussions regarding the experimental implementation of this proposal. We acknowledge support from the ERC Advanced Grant QENOCOBA under the EU Horizon 2020 programme (grant agreement 742102). J.A.-L. acknowledges support from “la Caixa” Foundation (ID 100010434) under fellowship LCF/BQ/ES18/11670016. Work at ICFO is supported by the Spanish Ministry of Economy and Competitiveness through the “Severo Ochoa” programme (SEV-2015-0522), Fundació Privada Cellex, and by Generalitat de Catalunya through the CERCA programme. A. G.-T. acknowledges support from the Spanish project PGC2018-094792-B-100 (MCIU/AEI/FEDER, EU) and from the CSIC Research Platform on Quantum Technologies PTI-001. T.S. is grateful to the Thousand-Youth-Talent Program of China. P.Z. was supported by the ERC Synergy Grant UQUAM and by SFB FoQus of the Austrian Science Foundation.
Author information
Authors and Affiliations
Contributions
J.A.-L., A.G.-T. and T.S. designed the model, developed the methods and analysed the data. J.A.-L. and A.G.-T. performed the calculations. J.A.-L., A.G.-T. and J.I.C. wrote the manuscript with input from all authors. J.I.C. and P.Z. conceived the study and were in charge of the overall direction and planning.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Results of the G-S algorithm.
a, b, We apply the G-S algorithm to identify the phase mask associated with a holographic 3D Coulomb potential on a lattice of N3 sites. Fixing the origin at the central site, we choose the nucleus position as n = [(2ndiv)−1, 0, 0] (the first coordinate is shifted so that the lattice induces a natural cutoff). a, An axial central cut of the potential (yellow markers) in direction z (see aligned set of sites in b; red), created by a phase mask composed of (ndivN) × (ndivN) cells for ndiv = 3 (see inset), compared to the objective Coulomb potential (blue solid line). In step (ii) of the algorithm, the Ewald sphere is discretized using a parallel projection, as in ref. 31. The field is initiated with random phases. Parameters: N = 30 and 7,000 iterations of the G-S algorithm. b, Location of the axial cut shown in a.
Extended Data Fig. 2 Numerical simulation of the adiabatic preparation of the ground state of H2 with the simulator (particularized for a 2D lattice).
Red dashed lines follow the adiabatic evolution of the initial state \(\left|{\psi }_{0}\right\rangle \) and arrows point to the direction of evolution. a, Preparation of the bosonic state through steps I(a)–I(c) (see Methods and Extended Data Table 1). Continuous lines indicate the exact energy of the two lowest energy states. For the adiabatic evolution we use Trotterized time as ΔtU = 0.5 and evolution with |ΔU|/(U2Δt) = 3 × 10−4. b, Steps II–III of the preparation of the fermionic state. In the simulation, we use the Trotterized time evolution in intervals of ΔtV0 = 0.05. In step II, the kinetic term is adiabatically introduced in steps of \(\Delta {t}_{{\rm{F}}}/({{\rm{V}}}_{0}^{2}\Delta t)=0.005\). In step III, the electronic repulsion is tuned up as \(\Delta V/({{\rm{V}}}_{0}^{2}\Delta t)=0.02\). Here yellow (blue) continuous lines follow the exact energy levels of Hqc, as calculated by imaginary-time evolution with (without) the effect of electronic repulsion. The top insets show the Mott excitation (a) fermionic population (b) in the lattice at the times indicated in the figure. The final point of the evolution shown in b corresponds to d/a0 = 1. Parameters: N = 60, U/Jc = 1.5, d/a = 10.
Supplementary information
Supplementary Information
This file contains Supplementary Text, Supplementary Figures 1 and 2, and additional references. This presents the numerical methods employed in this Letter, together with a derivation of the simulated Hamiltonian and conditions introduced in the main text
Rights and permissions
About this article
Cite this article
Argüello-Luengo, J., González-Tudela, A., Shi, T. et al. Analogue quantum chemistry simulation. Nature 574, 215–218 (2019). https://doi.org/10.1038/s41586-019-1614-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1614-4
This article is cited by
-
Advancements in Quantum Computing—Viewpoint: Building Adoption and Competency in Industry
Datenbank-Spektrum (2024)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
Practical quantum advantage in quantum simulation
Nature (2022)
-
Tuneable Gaussian entanglement in levitated nanoparticle arrays
npj Quantum Information (2022)
-
Engineering topological states in atom-based semiconductor quantum dots
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.