Abstract
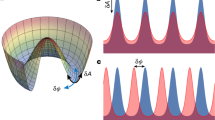
Supersolids are exotic materials combining the frictionless flow of a superfluid with the crystal-like periodic density modulation of a solid. The supersolid phase of matter was predicted 50 years ago1,2,3 for solid helium4,5,6,7,8. Ultracold quantum gases have recently been made to exhibit periodic order typical of a crystal, owing to various types of controllable interaction9,10,11,12,13. A crucial feature of a D-dimensional supersolid is the occurrence of D + 1 gapless excitations, reflecting the Goldstone modes associated with the spontaneous breaking of two continuous symmetries: the breaking of phase invariance, corresponding to the locking of the phase of the atomic wave functions at the origin of superfluid phenomena, and the breaking of translational invariance due to the lattice structure of the system. Such modes have been the object of intense theoretical investigations1,14,15,16,17,18, but they have not yet been observed experimentally. Here we demonstrate supersolid symmetry breaking through the appearance of two distinct compressional oscillation modes in a harmonically trapped dipolar Bose–Einstein condensate, reflecting the gapless Goldstone excitations of the homogeneous system. We observe that the higher-frequency mode is associated with an oscillation of the periodicity of the emergent lattice and the lower-frequency mode characterizes the superfluid oscillations. This work also suggests the presence of two separate quantum phase transitions between the superfluid, supersolid and solid-like configurations.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The datasets that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Andreev, A. F. & Lifshitz, I. M. Quantum theory of defects in crystals. Sov. Phys. JETP 29, 1107–1113 (1969).
Chester, G. V. Speculations on Bose–Einstein condensation and quantum crystals. Phys. Rev. A 2, 256–258 (1970).
Leggett, A. J. Can a solid be “superfluid”? Phys. Rev. Lett. 25, 1543–1546 (1970).
Boninsegni, M. & Prokof’ev, N. V. Colloquium: Supersolids: what and where are they? Rev. Mod. Phys. 84, 759 (2012).
Kim, E. & Chan, M. H. W. Probable observation of a supersolid helium phase. Nature 427, 225–227 (2004).
Balibar, S. The enigma of supersolidity. Nature 464, 176–182 (2010).
Kim, D. Y. & Chan, M. H. W. Absence of supersolidity in solid helium in porous Vycor glass. Phys. Rev. Lett. 109, 155301 (2012).
Nyéki, J. et al. Intertwined superfluid and density wave order in two-dimensional 4He. Nat. Phys. 13, 455–459 (2017).
Li, J.-R. et al. A stripe phase with supersolid properties in spin–orbit-coupled Bose–Einstein condensates. Nature 543, 91–94 (2017).
Léonard, J., Morales, A., Zupancic, P., Esslinger, T. & Donner, T. Supersolid formation in a quantum gas breaking a continuous translational symmetry. Nature 543, 87–90 (2017).
Tanzi, L. et al. Observation of a dipolar quantum gas with metastable supersolid properties. Phys. Rev. Lett. 122, 130405 (2019).
Böttcher, F. et al. Transient supersolid properties in an array of dipolar quantum droplets. Phys. Rev. X 9, 011051 (2019).
Chomaz, L. et al. Long-lived and transient supersolid behaviors in dipolar quantum gases. Phys. Rev. X 9, 021012 (2019).
Josserand, C., Pomeau, Y. & Rica, S. Coexistence of ordinary elasticity and superfluidity in a model of a defect-free supersolid. Phys. Rev. Lett. 98, 195301 (2007).
Watanabe, H. & Brauner, T. Spontaneous breaking of continuous translational invariance. Phys. Rev. D 85, 085010 (2012).
Kunimi, M. & Kato, Y. Mean-field and stability analyses of two-dimensional flowing soft-core bosons modeling a supersolid. Phys. Rev. B 86, 060510(R) (2012).
Saccani, S., Moroni, S. & Boninsegni, M. Excitation spectrum of a supersolid. Phys. Rev. Lett. 108, 175301 (2012).
Roccuzzo S. M. & Ancilotto, F. Supersolid behavior of a dipolar Bose-Einstein condensate confined in a tube. Phys. Rev. A 99, 041601(R) (2019).
Li, Y., Pitaevskii, L. P. & Stringari, S. Quantum tricriticality and phase transitions in spin-orbit-coupled Bose–Einstein condensates. Phys. Rev. Lett. 108, 225301 (2012).
Lang, J., Piazza, F. & Zwerger, W. Collective excitations and supersolid behavior of bosonic atoms inside two crossed optical cavities. New J. Phys. 19, 123027 (2017).
Pupillo, G., Micheli, A., Boninsegni, M., Lesanovsky, I. & Zoller, P. Strongly correlated gases of Rydberg-dressed atoms: quantum and classical dynamics. Phys. Rev. Lett. 104, 223002 (2010).
Macrì, T., Maucher, F., Cinti, F., & Pohl, T. Elementary excitations of ultracold soft-core bosons across the superfluid-supersolid phase transition. Phys. Rev. A 87, 061602 (2013).
Ancilotto, F., Rossi, M. & Toigo, F. Supersolid structure and excitation spectrum of soft-core bosons in three dimensions. Phys. Rev. A 88, 033618 (2013).
Lu, Z.-K., Li, Y., Petrov, D. S. & Shlyapnikov, G. V. Stable dilute supersolid of two-dimensional dipolar bosons. Phys. Rev. Lett. 115, 075303 (2015).
Stringari, S. Collective excitations of a trapped Bose-condensed gas. Phys. Rev. Lett. 77, 2360–2363 (1996).
Jin, D. S., Ensher, J. R., Matthews, M. R., Wieman, C. E. & Cornell, E. A. Collective excitations of a Bose-Einstein condensate in a dilute gas. Phys. Rev. Lett. 77, 420–423 (1996).
Mewes, M. O. et al. Collective excitations of a Bose-Einstein condensate in a magnetic trap. Phys. Rev. Lett. 77, 988–991 (1996).
Pitaevskii, L. & Stringari, S. Bose-Einstein Condensation and Superfluidity (Oxford Univ. Press, 2011).
Petter, D. et al. Probing the roton excitation spectrum of a stable dipolar Bose gas. Phys. Rev. Lett. 122, 183401 (2019).
Chomaz, L. et al. Observation of roton mode population in a dipolar quantum gas. Nat. Phys. 14, 442–446 (2018).
Lima, A. R. P. & Pelster, A. Beyond mean-field low-lying excitations of dipolar Bose gases. Phys. Rev. A 86, 063609 (2012).
Kadau, H. et al. Observing the Rosensweig instability of a quantum ferrofluid. Nature 530, 194–197 (2016).
Wenzel, M., Böttcher, F., Langen, T., Ferrier-Barbut, I. & Pfau, T. Striped states in a many-body system of tilted dipoles. Phys. Rev. A 96, 053630 (2017).
van Bijnen, R. M. W., Parker, N. G., Kokkelmans, S. J. J. M. F., Martin, A. M. & O’Dell, D. H. J. Collective excitation frequencies and stationary states of trapped dipolar Bose-Einstein condensates in the Thomas-Fermi regime. Phys. Rev. A 82, 033612 (2010).
Ronen, S., Bortolotti, D. C. E. & Bohn, J. L. Bogoliubov modes of a dipolar condensate in a cylindrical trap. Phys. Rev. A 74, 013623 (2006).
Blakie, P.E., Baillie, D. & Bisset, R. N. Roton spectroscopy in a harmonically trapped dipolar Bose-Einstein condensate. Phys. Rev. A 86, 021604 (2012).
Léonard, J., Morales, A., Zupancic, P., Donner, T. & Esslinger, T. Monitoring and manipulating Higgs and Goldstone modes in a supersolid quantum gas. Science 358, 1415–1418 (2017).
Guo, M. et al. The low-energy Goldstone mode in a trapped dipolar supersolid. Nature https://doi.org/10.1038/s41586-019-1569-5 (2019).
Natale, G. et al. Excitation spectrum of a trapped dipolar supersolid and its experimental evidence. Phys. Rev. Lett. 123, 050402 (2019).
Menotti, C. & Stringari, S. Collective oscillations of a one-dimensional trapped Bose-Einstein gas. Phys. Rev. A 66, 043610 (2002).
Matveeva, N., Recati, A. & Stringari, S. Dipolar drag in bilayer harmonically trapped gases. Eur. Phys. J. D 65, 219–222 (2011).
Lucioni, E. et al. Dysprosium dipolar Bose-Einstein condensate with broad Feshbach resonances. Phys. Rev. A 97, 060701 (2018).
Böttcher, F. et al. Quantum correlations in dilute dipolar quantum droplets beyond the extended Gross-Pitaevskii equation. Preprint at https://arxiv.org/abs/1904.10349 (2019).
Giovanazzi, S. et al. Expansion dynamics of a dipolar Bose-Einstein condensate. Phys. Rev. A 74, 013621 (2006).
Giorgini, S. Collisionless dynamics of dilute Bose gases: Role of quantum and thermal fluctuations. Phys. Rev. A 61, 063615 (2000).
Acknowledgements
This work received funding from the EC-H2020 research and innovation program (grant number 641122-QUIC). We acknowledge discussions with R. Citro and J. G. Maloberti and technical assistance from A. Barbini, F. Pardini, M. Tagliaferri and M. Voliani. S.M.R., A.R. and S.S. acknowledge funding from Provincia Autonoma di Trento and the Q@TN initiative. We acknowledge discussions with the participants of the Stuttgart meeting on ‘Perspectives for supersolidity in dipolar droplet arrays’.
Author information
Authors and Affiliations
Contributions
L.T., E.L., F.F., A.F., C.G. and G.M. conceived the experimental investigation, performed the measurements and the experimental data analysis. S.M.R., A.R. and S.S. conceived the theoretical investigation, performed the simulations and the theoretical data analysis. All authors contributed to discussions and writing of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Peer review information Nature thanks Sean Mossman, Georgy Shlyapnikov and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Fig. 1 Peak amplitude and relative distance.
In the supersolid regime, the axial breathing mode bifurcates into higher- and lower-frequency modes, mainly coupled to the relative distance between the density peaks and to their amplitude, respectively. a, b, Time evolution of the relative distance d(t) between two density peaks (a) and its Fourier transform, dominated by a peak at the higher frequency (red arrow) (b). c, d, Time evolution of the peak density amplitude A(t) (c) and its Fourier transform, dominated by the lower-frequency mode (blue arrow) (d).
Extended Data Fig. 2 Examples of small- and large-amplitude oscillations.
a, b, Typical false-colour experimental distributions in the \(({k}_{x},{k}_{y})\) plane for the BEC regime close to the roton instability, \({{\epsilon }}_{{\rm{dd}}}\) = 1.35(3) (a) and the droplet regime, \({{\epsilon }}_{{\rm{dd}}}\) = 1.50(5) (b). c, d, Small-amplitude oscillation of \({\sigma }_{k}(t)\) under the same conditions, \({{\epsilon }}_{{\rm{dd}}}\) = 1.35(3) (c) and \({{\epsilon }}_{{\rm{dd}}}\) = 1.50(5) (d). e, f, Large-amplitude oscillation of \({\sigma }_{k}(t)\) for the BEC regime, \({{\epsilon }}_{{\rm{dd}}}\) = 1.21(2) (e) and the supersolid regime, \({{\epsilon }}_{{\rm{dd}}}\) = 1.38(2) (f). In the supersolid regime, we observe a small frequency shift in the oscillation of \({\sigma }_{k}(t)\) over time: we fit ω/ωx = 1.43(1) up to about 150 ms (blue line), and ω/ωx = 1.48(2) from 150 ms onwards (red line). Error bars represent the standard deviation of 4–8 measurements.
Extended Data Fig. 3 Large temperature measurements in the BEC regime.
a, b, Measured frequency (a) and measured damping time (b) of the axial breathing mode at \({{\epsilon }}_{{\rm{dd}}}\) ≈ 1.2 for increasing temperature. The measured frequency for a thermal gas (red dot) is compatible with ω/ωx = 2, demonstrating the collisionless nature of the system and the breaking of phase invariance for the BEC. Error bars represent the standard deviation of 4–8 measurements.
Rights and permissions
About this article
Cite this article
Tanzi, L., Roccuzzo, S.M., Lucioni, E. et al. Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas. Nature 574, 382–385 (2019). https://doi.org/10.1038/s41586-019-1568-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1568-6
This article is cited by
-
Giant magnetocaloric effect in spin supersolid candidate Na2BaCo(PO4)2
Nature (2024)
-
Heating a dipolar quantum fluid into a solid
Nature Communications (2023)
-
Supersolidity in ultracold dipolar gases
Nature Reviews Physics (2023)
-
Apparatus for producing a \(^{168}\hbox {Er}\) Bose–Einstein condensate
Journal of the Korean Physical Society (2023)
-
Spin supersolidity in nearly ideal easy-axis triangular quantum antiferromagnet Na2BaCo(PO4)2
npj Quantum Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.