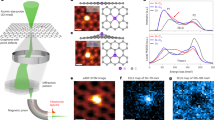
Abstract
Propagating atomic vibrational waves—phonons—determine important thermal, mechanical, optoelectronic and transport characteristics of materials. Thus a knowledge of phonon dispersion (that is, the dependence of vibrational energy on momentum) is a key part of our understanding and optimization of a material’s behaviour. However, the phonon dispersion of a free-standing monolayer of a two-dimensional material such as graphene, and its local variations, have remained elusive for the past decade because of the experimental limitations of vibrational spectroscopy. Even though electron energy loss spectroscopy (EELS) in transmission has recently been shown to probe local vibrational charge responses1,2,3,4, such studies are still limited by momentum space integration due to the focused beam geometry; they are also restricted to polar materials such as boron nitride or oxides1,2,3,4, in which huge signals induced by strong dipole moments are present. On the other hand, measurements on graphene performed by inelastic X-ray (neutron) scattering spectroscopy5,6,7 or EELS in reflection8,9 do not have any spatial resolution and require large microcrystals. Here we provide a new pathway to determine phonon dispersions down to the scale of an individual free-standing graphene monolayer by mapping the distinct vibrational modes for a large momentum transfer. The measured scattering intensities are accurately reproduced and interpreted with density functional perturbation theory10. Additionally, a nanometre-scale mapping of selected momentum-resolved vibrational modes using graphene nanoribbon structures has enabled us to spatially disentangle bulk, edge and surface vibrations. Our results are a proof-of-principle demonstration of the feasibility of studying local vibrational modes in two-dimensional monolayer materials at the nanometre scale.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.
Code availability
Quantum ESPRESSO is an open-source suite of computational tools available at www.quantum-espresso.org. The PH package was modified to print out the valence-electron density response to ionic displacements. The post-processing code used to simulate the EEL spectra will be included in a next release of the PH package.
References
Krivanek, O. L. et al. Vibrational spectroscopy in the electron microscope. Nature 514, 209–212 (2014).
Lagos, M. J., Trügler, A., Hohenester, U. & Batson, P. E. Mapping vibrational surface and bulk modes in a single nanocube. Nature 543, 529–532 (2017).
Hage, F. S. et al. Nanoscale momentum-resolved vibrational spectroscopy. Sci. Adv. 1, eaar7495 (2018).
Dwyer, C. et al. Electron-beam mapping of vibrational modes with nanometer spatial resolution. Phys. Rev. Lett. 117, 256101 (2016).
Maultzsch, J., Reich, S., Thomsen, C., Requardt, H. & Ordejón, P. Phonon dispersion in graphite. Phys. Rev. Lett. 92, 075501 (2004).
Mohr, M. et al. Phonon dispersion of graphite by inelastic X-ray scattering. Phys. Rev. B 76, 035439 (2007).
Nicklow, R., Wakabayashi, N. & Smith, H. G. Lattice dynamics of pyrolytic graphite. Phys. Rev. B 5, 4951–4962 (1972).
Vig, S. et al. Measurement of the dynamic charge response of materials using low-energy, momentum-resolved electron energy-loss spectroscopy (M-EELS). SciPost Phys. 3, 026 (2017).
Oshima, C., Aizawa, T., Souda, R., Ishizawa, Y. & Sumiyoshi, Y. Surface phonon dispersion curves of graphite (0001) over the entire energy region. Solid State Commun. 65, 1601–1604 (1988).
Giannozzi, P., De Gironcoli, S., Pavone, P. & Baroni, S. Ab initio calculation of phonon dispersions in semiconductors. Phys. Rev. B 43, 7231–7242 (1991).
Van Hove, L. Correlations in space and time and Born approximation scattering in systems of interacting particles. Phys. Rev. 95, 249–262 (1954).
Roth, F., König, A., Fink, J., Büchner, B. & Knupfer, M. Electron energy-loss spectroscopy: a versatile tool for the investigations of plasmonic excitations. J. Electron Spectrosc. Relat. Phenom. 195, 85–95 (2014).
Nicholls, R. J. et al. Theory of momentum-resolved phonon spectroscopy in the electron microscope. Phys. Rev. B 99, 094105 (2019).
Vogl, P. Microscopic theory of electron-phonon interaction in insulators or semiconductors. Phys. Rev. B 13, 694–704 (1976).
Falter, C., Ludwig, W., Maradudin, A. A., Selmke, M. & Zierau, W. Valence charge density and effective charges within the density-response theory. Phys. Rev. B 32, 6510–6517 (1985).
Ghosez, P., Michenaud, J.-P. & Gonze, X. Dynamical atomic charges: the case of ABO3 compounds. Phys. Rev. B 58, 6224–6240 (1998).
Muller, D. & Silcox, J. Delocalization in inelastic scattering. Ultramicroscopy 59, 195–213 (1995).
Hage, F. S., Kepaptsoglou, D. M., Ramasse, Q. M. & Allen, L. J. Phonon spectroscopy at atomic resolution. Phys. Rev. Lett. 122, 016103 (2019).
Venkatraman, K., Levin, B. D. A., March, K., Rez, P. & Crozier, P. A. Vibrational spectroscopy at atomic resolution with electron impact scattering. Preprint at https://arXiv.org/abs/1812.08895 (2018).
Sohier, T., Gibertini, M., Calandra, M., Mauri, F. & Marzari, N. Breakdown of optical phonons’ splitting in two-dimensional materials. Nano Lett. 17, 3758–3763 (2017).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Acknowledgements
This work was supported by KAKENHI (17H04797 and 16H06333) and by the European Graphene Flagship Core 2 grant no. 785219. T.P. thanks the FWF for funding (P27769-N20). P.B. and F.M. acknowledge CINECA awards under the ISCRA initiative (grants HP10B3EDF2 and HP10BSZ6LY) for making available high-performance computing resources and support. We thank P. Ayala for fruitful discussions.
Author information
Authors and Affiliations
Contributions
R.S., S.M., T.P. and K.S. designed the experiments. R.S. performed EELS measurements. R.S. and T.P. analysed data. P.B. and F.M. established the theory and performed ab initio calculations. R.S., T.P., P.B., F.M. and K.S. co-wrote the paper. All authors commented on manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Raw EEL spectra including quasi-elastic lines.
a–d, Series of momentum-resolved EEL spectra along the ΓΜΓΜ (a, c) and ΓΚΜΚΓ (b, d) directions taken from graphite (a, b) and hBN (c, d) flakes.
Extended Data Fig. 2 Line shape analysis of the measured spectra of graphite.
Shown are typical examples of line shape analysis of the EEL spectra of graphite at q = 2.25, 3.25 and 4.00 Å−1 (left, middle and right panels, respectively). Each component (modes LA, LO, TO, LA; purple lines) is fitted with a Voigtian including the fixed experimental broadening factor (30–40 meV). The data points and the fitting lines are shown by black dots and blue lines, respectively.
Extended Data Fig. 3 Phonon dispersion of hBN and graphite along the ΓΚΜΚΓ direction.
a, b, Series of momentum-resolved EEL spectra (left) and simulated spectra (right) along the ΓΚΜΚΓ direction (from top to bottom) for graphite and hBN, respectively. The quasi-elastic lines have been subtracted. (The raw data including the quasi-elastic lines are shown in Extended Data Fig. 1). The spectra are recorded at every 0.25 Å−1 from q = 0 to 5.00 Å−1 in the ΓΜ direction and at the second Γ point of graphite (5.11 Å−1). The spectra at every Γ point (red lines) include the Bragg reflection spots. c–f, Intensity colour maps of graphite (c, e) and hBN (d, f) constructed from the measured EEL spectra (c, d) and from the simulated spectra (e, f) are shown with the simulated phonon dispersion curves (solid lines). The peak positions extracted from the measured spectra by the line shape analysis are indicated by the open triangles in c and d.
Extended Data Fig. 4 Bubble plots of the phonon dispersion of graphite and hBN.
Left column, along the ΓMΓM direction; right column, along the ΓKMKΓ direction. These plots are obtained by line shape analysis of the measured spectra (‘Experiment’; first and third rows) and from the simulation (DFPT; second and fourth rows). The size (cross-section) of each point (the ‘bubble’) corresponds to the intensity, which is normalized by the highest peak at each measured (or calculated) q.
Extended Data Fig. 5 The contribution of out-of-plane modes induced by sample tilting.
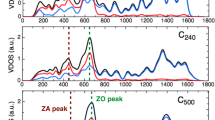
Left, middle, right, simulated spectra of hBN at q = 1, 1.75, 2.5 Å−1 respectively along the ΓΚΜΚΓ line: each panel shows the effect of the tilting angle. ZA and ZO modes are gradually activated as the tilting angle increases. Bars indicate the mode-resolved calculated intensities at each phonon frequency that are then broadened with a 25-meV Lorentzian, resulting in the simulated spectra.
Extended Data Fig. 6 q-dependence of effective charges and total intensity for phonon EEL spectra.
Top, the evolution of effective charges in both hBN and graphite as a function of q are shown along the ΓΜΓΜ (left panel) and ΓΚΜΚΓ (right panel) directions. Solid (dashed) lines correspond to the real (imaginary) part of the effective charge. Despite graphite hosting two inequivalent carbon ions (C1 and C2), their effective charges are substantially indistinguishable except for very small momenta, where tiny differences only can be seen (inset). Bottom, the total intensity for graphite (black) and hBN (red) as a function of momentum transfer obtained from the experiments (filled circles with dotted lines) and from DFPT calculations (solid lines), evaluated as \(I({\boldsymbol{q}})={\int }_{0}^{{\rm{\infty }}}{\rm{d}}\omega \frac{{{\rm{d}}}^{2}\sigma }{{\rm{d}}\Omega {\rm{d}}\omega }({\boldsymbol{q}},\omega )\). The singular behaviour of the theoretical total intensity observed at Γ points in higher-order Brillouin zones can be ascribed to the 1/ωqν dependence of the differential cross-section, which diverges for LA modes (notice that this diverging behaviour does not appear if the total intensity is evaluated with a low-frequency cut-off ωcut, as shown in Fig. 2a). A renormalized intensity defined as \(I({\boldsymbol{q}})\propto \sum _{\nu }{|\sum _{I}\frac{1}{\sqrt{{M}_{I}}}{{\boldsymbol{Z}}}_{I}({\boldsymbol{q}})\cdot {{\boldsymbol{e}}}_{{\boldsymbol{q}},\nu }^{I}{{\rm{e}}}^{-i{\boldsymbol{q}}\cdot {{\boldsymbol{\tau }}}_{I}}|}^{2}\) is also shown in the bottom panels. This highlights the non-trivial momentum-dependence of EEL intensity that stems from effective charges when the trivial momentum and phonon dependencies 1/q2 and (1+nqv)/ωqv, respectively, are neglected. A blue line scaling as 1/q2 (q2) is also shown as a reference for total (renormalized) intensities.
Extended Data Fig. 7 Phonon EEL spectra of monolayer graphene.
a–d, Series of momentum-resolved EEL spectra along ΓΜΓΜ (a), ΓΚΜΚΓ (b), asymmetric ΓΚ (c) and ΚΚ (d) directions taken from monolayer graphene. The quasi-elastic lines have been subtracted.
Extended Data Fig. 8 Bubble plots for the phonon dispersion of monolayer graphene.
Each vertical pair of panels is labelled at the top by the sample material and the direction: in each of these vertical pairs, the top panel exhibits the plots obtained by line shape analysis of the measured spectra, and the bottom panel presents the plots obtained by simulation (DFPT). The directions are ΓΜΓΜ (top left), ΓΚΜΚΓ (top right), Γ → the third-closest Κ (bottom left) and ΚΚ (bottom right). The plot size (cross-section) corresponds to the intensity, which has been normalized by the highest peak at each measured or calculated q. In the ΓΜΓΜ line, LO modes (170–200 meV) are visible at the second Brillouin zone along with LA modes that show up throughout. In the ΓΚΜΚΓ direction, the TO mode is additionally seen at the second Brillouin zone along the KMK line for both experiment and simulation. In the low-symmetry line (Γ → the third-closest Κ), the TA mode shows up in the latter half of the second Brillouin zone. The dispersion along the ΚΚ direction that cuts across the second Brillouin zone shows the LO mode in the first half and the TO mode in the second half in the simulation, while this asymmetric behaviour is not clearly seen in the experiment. LA and TA modes are also activated weakly at the middle of the ΚΚ line in both experiment and simulation.
Extended Data Fig. 9 Momentum mapping of vibrations in graphite.
Shown are EELS spectra along two different directions: Γ → the third-closest Κ (‘Graphite asymmetric ΓK’; top four panels) and ΚΚ (‘Graphite ΚΚ’; bottom four panels). Within each group of four panels, the top two exhibit the intensity colour map (left) and bubble plots (right) obtained by line shape analysis of the measured spectra (Exp.): the bottom two present intensity colour maps and bubble plots obtained by the simulation (DFPT).
Extended Data Fig. 10 Position mapping of vibrations in monolayer graphene.
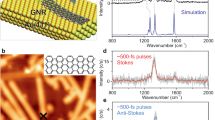
a, An STEM image of free-standing graphene; it has two-, three- and four-layer regions as well as a single-layer region (b). c, Typical EEL spectrum at q = 3.5 Å−1 taken from a clean single-layer region where 16 pixels are integrated. The phonon response there consists of two broad peaks: peak A (between 60 and 100 meV), which is related to the LA/ZO mode as well as the edge and sp3 defect contributions; and peak B (at about 200 meV), which is related to the LO/TO mode. d, e, Corresponding position mappings of vibration modes A and B, respectively (dashed lines show information from b). The integration windows for the mappings are also shown by the light green and light blue stripes in c. f, Intensity profiles of vibration modes A and B along the orange line in a across the two impurity-decorated grain boundaries. The intensity of the LO/TO mode (B) is simply proportional to the layer number (the specimen thickness), while the lower-energy mode (A) clearly shows higher intensity at the edges of two- and four-layer regions. Interestingly, no obvious intensity enhancement can be seen at the edge of the single-layer region. In addition, we found intensity variations of the low-energy mode at grain boundaries, as shown in f, although their interpretation is more complicated because there must be contributions from different momentum transfers derived from domains with different orientations.
Rights and permissions
About this article
Cite this article
Senga, R., Suenaga, K., Barone, P. et al. Position and momentum mapping of vibrations in graphene nanostructures. Nature 573, 247–250 (2019). https://doi.org/10.1038/s41586-019-1477-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1477-8
This article is cited by
-
Observation of the nonanalytic behavior of optical phonons in monolayer hexagonal boron nitride
Nature Communications (2024)
-
Single-atom vibrational spectroscopy with chemical-bonding sensitivity
Nature Materials (2023)
-
Nanoscale imaging of phonon dynamics by electron microscopy
Nature (2022)
-
AtomAI framework for deep learning analysis of image and spectroscopy data in electron and scanning probe microscopy
Nature Machine Intelligence (2022)
-
Imaging of isotope diffusion using atomic-scale vibrational spectroscopy
Nature (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.