Abstract
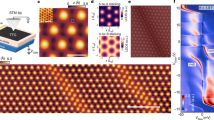
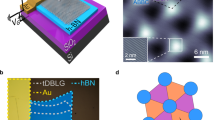
The electronic properties of heterostructures of atomically thin van der Waals crystals can be modified substantially by moiré superlattice potentials from an interlayer twist between crystals1,2. Moiré tuning of the band structure has led to the recent discovery of superconductivity3,4 and correlated insulating phases5 in twisted bilayer graphene (TBG) near the ‘magic angle’ of twist of about 1.1 degrees, with a phase diagram reminiscent of high-transition-temperature superconductors. Here we directly map the atomic-scale structural and electronic properties of TBG near the magic angle using scanning tunnelling microscopy and spectroscopy. We observe two distinct van Hove singularities (VHSs) in the local density of states around the magic angle, with an energy separation of 57 millielectronvolts that drops to 40 millielectronvolts with high electron/hole doping. Unexpectedly, the VHS energy separation continues to decrease with decreasing twist angle, with a lowest value of 7 to 13 millielectronvolts at a magic angle of 0.79 degrees. More crucial to the correlated behaviour of this material, we find that at the magic angle, the ratio of the Coulomb interaction to the bandwidth of each individual VHS (U/t) is maximized, which is optimal for electronic Cooper pairing mechanisms. When doped near the half-moiré-band filling, a correlation-induced gap splits the conduction VHS with a maximum size of 6.5 millielectronvolts at 1.15 degrees, dropping to 4 millielectronvolts at 0.79 degrees. We capture the doping-dependent and angle-dependent spectroscopy results using a Hartree–Fock model, which allows us to extract the on-site and nearest-neighbour Coulomb interactions. This analysis yields a U/t of order unity indicating that magic-angle TBG is moderately correlated. In addition, scanning tunnelling spectroscopy maps reveal an energy- and doping-dependent three-fold rotational-symmetry breaking of the local density of states in TBG, with the strongest symmetry breaking near the Fermi level and further enhanced when doped to the correlated gap regime. This indicates the presence of a strong electronic nematic susceptibility or even nematic order in TBG in regions of the phase diagram where superconductivity is observed.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data presented in this work is available upon reasonable request to A.N.P.
Code availability
Code for the analysis described in Methods section ‘Anisotropy quantification technique’ and other analyses presented in this paper are available upon reasonable request.
References
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Lopes dos Santos, J. M. B., Peres, N. M. R. & Castro Neto, A. H. Graphene bilayer with a twist: electronic structure. Phys. Rev. Lett. 99, 256802 (2007).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Wu, F., Lovorn, T., Tutuc, E. & MacDonald, A. H. Hubbard model physics in transition metal dichalcogenide moiré bands. Phys. Rev. Lett. 121, 026402 (2018).
Xian, L., Kennes, D. M., Tancogne-Dejean, N., Altarelli, M. & Rubio, A. Multi-flat bands and strong correlations in twisted bilayer boron nitride. Preprint at https://arxiv.org/abs/1812.08097 (2018).
Wong, D. et al. Local spectroscopy of moiré-induced electronic structure in gate-tunable twisted bilayer graphene. Phys. Rev. B 92, 155409 (2015).
Li, G. et al. Observation of Van Hove singularities in twisted graphene layers. Nat. Phys. 6, 109–113 (2010).
Brihuega, I. et al. Unraveling the intrinsic and robust nature of van Hove singularities in twisted bilayer graphene by scanning tunneling microscopy and theoretical analysis. Phys. Rev. Lett. 109, 196802 (2012).
Yin, L.-J., Qiao, J.-B., Zuo, W.-J., Li, W.-T. & He, L. Experimental evidence for non-Abelian gauge potentials in twisted graphene bilayers. Phys. Rev. B 92, 081406 (2015).
Yuan, N. F. Q. & Fu, L. Model for the metal-insulator transition in graphene superlattices and beyond. Phys. Rev. B 98, 045103 (2018).
Po, H. C., Zou, L. J., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).
Padhi, B., Setty, C. & Phillips, P. W. Doped twisted bilayer graphene near magic angles: proximity to Wigner crystallization, not Mott insulation. Nano Lett. 18, 6175–6180 (2018).
Isobe, H., Yuan, N. F. Q. & Fu, L. Unconventional superconductivity and density waves in twisted bilayer graphene. Preprint at https://arxiv.org/abs/1805.06449 (2018).
Kennes, D. M., Lischner, J. & Karrasch, C. Strong correlations and d+id superconductivity in twisted bilayer graphene. Preprint at https://arxiv.org/abs/1805.06310 (2018).
Huang, S. et al. Topologically protected helical states in minimally twisted bilayer graphene. Phys. Rev. Lett. 121, 037702 (2018).
Yoo, H. et al. Atomic and electronic reconstruction at van der Waals interface in twisted bilayer graphene. Preprint at https://arxiv.org/abs/1804.03806 (2018).
Carr, S., Fang, S., Zhu, Z. & Kaxiras, E. An exact continuum model for low-energy electronic states of twisted bilayer graphene. Preprint at https://arxiv.org/abs/1901.03420 (2019).
Trambly de Laissardière, G., Mayou, D. & Magaud, L. Localization of Dirac electrons in rotated graphene bilayers. Nano Lett. 10, 804–808 (2010).
Grüneis, A. et al. Electron-electron correlation in graphite: a combined angle-resolved photoemission and first-principles study. Phys. Rev. Lett. 100, 037601 (2008).
Trambly de Laissardière, G., Mayou, D. & Magaud, L. Numerical studies of confined states in rotated bilayers of graphene. Phys. Rev. B 86, 125413 (2012).
Xia, F., Farmer, D. B., Lin, Y.-m. & Avouris, P. Graphene field-effect transistors with high on/off current ratio and large transport band gap at room temperature. Nano Lett. 10, 715–718 (2010).
Cao, Y. et al. Strange metal in magic-angle graphene with near Planckian dissipation. Preprint at https://arxiv.org/abs/1901.03710 (2019).
Koralek, J. D. et al. Laser based angle-resolved photoemission, the sudden approximation, and quasiparticle-like spectral peaks in BSCCO. Phys. Rev. Lett. 96, 017005 (2006).
Mo, S. K. et al. Prominent quasiparticle peak in the photoemission spectrum of the metallic phase of V2O3. Phys. Rev. Lett. 90, 186403 (2003).
Valla, T. et al. Coherence–incoherence and dimensional crossover in layered strongly correlated metals. Nature 417, 627–630 (2002).
Rosenthal, E. P. et al. Visualization of electron nematicity and unidirectional antiferroic fluctuations at high temperatures in NaFeAs. Nat. Phys. 10, 225–232 (2014).
Li, S.-Y. et al. Evidence of electron-electron interactions around Van Hove singularities of a graphene Moiré superlattice. Preprint at https://arxiv.org/abs/1702.03501 (2017).
Andrade, E. F. et al. Visualizing the nonlinear coupling between strain and electronic nematicity in the iron pnictides by elasto-scanning tunneling spectroscopy. Preprint at https://arxiv.org/abs/1812.05287 (2018).
Kim, Y. et al. Charge inversion and topological phase transition at a twist angle induced van Hove singularity of bilayer graphene. Nano Lett. 16, 5053–5059 (2016).
Girit, Ç. Ö. & Zettl, A. Soldering to a single atomic layer. Appl. Phys. Lett. 91, 193512 (2007).
Wang, Z. F., Liu, F. & Chou, M. Y. Fractal Landau-level spectra in twisted bilayer graphene. Nano Lett. 12, 3833–3838 (2012).
Acknowledgements
We thank A. Millis, J. Schmalian, L. Fu, R. Fernandes and S. Todadri for discussions. This work is supported by the Programmable Quantum Materials (Pro-QM) programme at Columbia University, an Energy Frontier Research Center established by the Department of Energy (grant DE-SC0019443). Equipment support is provided by the Office of Naval Research (grant N00014-17-1-2967) and Air Force Office of Scientific Research (grant FA9550-16-1-0601). Support for sample fabrication at Columbia University is provided by the NSF MRSEC programme through Columbia in the Center for Precision Assembly of Superstratic and Superatomic Solids (DMR-1420634). Theoretical work was supported by the European Research Council (ERC-2015-AdG694097). The Flatiron Institute is a division of the Simons Foundation. L.X. acknowledges the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement number 709382 (MODHET). A.N.P. and A.R. acknowledge support from the Max Planck—New York City Center for Non-Equilibrium Quantum Phenomena. D.M.K. acknowledges funding from the Deutsche Forschungsgemeinschaft through the Emmy Noether programme (KA 3360/2-1). C.D. acknowledges support by the Army Research Office under W911NF-17-1-0323 and The David and Lucile Packard foundation.
Author information
Authors and Affiliations
Contributions
A.K. performed STM measurements. L.J.M., M.Y. and S.C. fabricated samples for STM measurements. A.K. and L.J.M. performed experimental data analysis. K.W. and T.T. provided hBN crystals. D.M.K. and L.X. performed theoretical calculations. J.H., C.D., A.R. and A.N.P. advised. A.K. wrote the manuscript with assistance from all authors.
Corresponding authors
Ethics declarations
Competing interests
: The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 0.79° LDOS doping dependence.
a, STS LDOS as a function of doping at a 0.79° TBG AA site for a doping range of −0.95ns to 0.8ns (ns being full filling of the moiré band with four electrons or holes). Spectra were taken in a closed loop at 100-meV and 50-pA setpoints with a 0.5-meV oscillation. b, Experimental VHS separation versus doping (bottom axis) and theoretical mean-field VHS separation as a function of chemical potential (Ed − μ) relative to charge neutrality (top axis) for the 0.79° doping-dependent LDOS. c, LDOS comparison of the correlated gap at half-filling (−0.5ns) in 1.15° TBG and 0.79° TBG. d, Peak-to-peak gap size as a function of doping, offset to half-filling (0.5ns) for 1.15° and 0.79°, where x is additional carrier doping in carriers per square centimetre around half-filling. e, Comparison of 0.79°, 1.15° and 1.10° LDOS when doped near the Fermi level, which is 0 V in the plot. The doping level of each curve is indicated in the legend. Error bars in b and d are estimated from the sum of squares of the lock-in oscillation (0.5 meV for 1.15° and 1 meV for 0.79°) used to determine feature positions.
Extended Data Fig. 2 Asymmetry in valence VHS with doping.
Half-widths of the trailing edge and leading edge of the valence VHS as a function of doping in the 1.15° sample. Error bars are estimated from the sum of squares of the lock-in oscillation (0.5 meV) used, which determines the peak half-width position.
Supplementary information
Supplementary Information
Supplementary Notes 1-10 including Supplementary Figures 1-10 and Supplementary References.
Rights and permissions
About this article
Cite this article
Kerelsky, A., McGilly, L.J., Kennes, D.M. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019). https://doi.org/10.1038/s41586-019-1431-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1431-9
This article is cited by
-
Direct observation of a magnetic-field-induced Wigner crystal
Nature (2024)
-
Manipulation of chiral interface states in a moiré quantum anomalous Hall insulator
Nature Physics (2024)
-
Terahertz linear/non-linear anomalous Hall conductivity of moiré TMD hetero-nanoribbons as topological valleytronics materials
Scientific Reports (2024)
-
Local atomic stacking and symmetry in twisted graphene trilayers
Nature Materials (2024)
-
Vestigial singlet pairing in a fluctuating magnetic triplet superconductor and its implications for graphene superlattices
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.