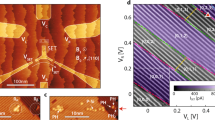
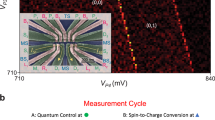
Abstract
Electron spin qubits formed by atoms in silicon have large (tens of millielectronvolts) orbital energies and weak spin–orbit coupling, giving rise to isolated electron spin ground states with coherence times of seconds1,2. High-fidelity (more than 99.9 per cent) coherent control of such qubits has been demonstrated3, promising an attractive platform for quantum computing. However, inter-qubit coupling—which is essential for realizing large-scale circuits in atom-based qubits—has not yet been achieved. Exchange interactions between electron spins4,5 promise fast (gigahertz) gate operations with two-qubit gates, as recently demonstrated in gate-defined silicon quantum dots6,7,8,9,10. However, creating a tunable exchange interaction between two electrons bound to phosphorus atom qubits has not been possible until now. This is because it is difficult to determine the atomic distance required to turn the exchange interaction on and off while aligning the atomic circuitry for high-fidelity, independent spin readout. Here we report a fast (about 800 picoseconds) \(\sqrt{{\bf{SWAP}}}\) two-qubit exchange gate between phosphorus donor electron spin qubits in silicon using independent single-shot spin readout with a readout fidelity of about 94 per cent on a complete set of basis states. By engineering qubit placement on the atomic scale, we provide a route to the realization and efficient characterization of multi-qubit quantum circuits based on donor qubits in silicon.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data pertaining to this study are available from the corresponding author upon reasonable request.
References
Kane, B. E. A silicon-based nuclear spin quantum computer. Nature 393, 133–137 (1998).
Muhonen, J. T. et al. Storing quantum information for 30 seconds in a nanoelectronic device. Nat. Nanotechnol. 9, 986–991 (2014).
Muhonen, J. T. et al. Quantifying the quantum gate fidelity of single-atom spin qubits in silicon by randomized benchmarking. J. Phys. Condens. Matter 27, 154205 (2015).
Hill, C. D. et al. Global control and fast solid-state donor electron spin quantum computing. Phys. Rev. B 72, 045350 (2005).
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998).
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015).
Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science 359, 439–442 (2018).
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature 555, 633–637 (2018).
Brunner, R. et al. Two-qubit gate of combined single-spin rotation and interdot spin exchange in a double quantum dot. Phys. Rev. Lett. 107, 146801 (2011).
Huang, W. et al. Fidelity benchmarks for two-qubit gates in silicon. Nature 569, 532–536 (2019).
Meunier, T., Calado, V. E. & Vandersypen, L. M. K. Efficient controlled-phase gate for single-spin qubits in quantum dots. Phys. Rev. B 83, 121403 (2011).
Kalra, R., Laucht, A., Hill, C. D. & Morello, A. Robust two-qubit gates for donors in silicon controlled by hyperfine interactions. Phys. Rev. X 4, 021044 (2014).
Hile, S. J. et al. Radio frequency reflectometry and charge sensing of a precision placed donor in silicon. Appl. Phys. Lett. 107, 093504 (2015).
Weber, B. et al. Spin blockade and exchange in Coulomb-confined silicon double quantum dots. Nat. Nanotechnol. 9, 430–435 (2014).
Yoneda, J. et al. A quantum-dot spin qubit with coherence limited by charge noise and fidelity higher than 99.9%. Nat. Nanotechnol. 13, 102–106 (2018).
Dial, O. E. et al. Charge noise spectroscopy using coherent exchange oscillations in a singlet-triplet qubit. Phys. Rev. Lett. 110, 146804 (2013).
Nowack, K. C. et al. Single-shot correlations and two-qubit gate of solid-state spins. Science 333, 1269–1272 (2011).
Broome, M. A. et al. High-fidelity single-shot singlet-triplet readout of precision-placed donors in silicon. Phys. Rev. Lett. 119, 046802 (2017).
Broome, M. A. et al. Two-electron spin correlations in precision placed donors in silicon. Nat. Commun. 9, 980 (2018).
Hsueh, Y.-L. et al. Spin-lattice relaxation times of single donors and donor clusters in silicon. Phys. Rev. Lett. 113, 246406 (2014).
Koiller, B., Hu, X. & Das Sarma, S. Exchange in silicon-based quantum computer architecture. Phys. Rev. Lett. 88, 027903 (2001).
Wang, Y. et al. Highly tunable exchange in donor qubits in silicon. npj Quantum Inf. 2, 16008 (2016).
Wang, Y., Chen, C.-Y., Klimeck, G., Simmons, M. Y. & Rahman, R. Characterizing Si:P quantum dot qubits with spin resonance techniques. Sci. Rep. 6, 31830 (2016); corrigendum 6, 38120 (2016).
Watson, T. F., Weber, B., House, M. G., Büch, H. & Simmons, M. Y. High-fidelity rapid initialization and read-out of an electron spin via the single donor D− charge state. Phys. Rev. Lett. 115, 166806 (2015).
Watson, T. F. et al. Atomically engineered electron spin lifetimes of 30 s in silicon. Sci. Adv. 3, e1602811 (2017).
Politi, A., Cryan, M. J., Rarity, J. G., Yu, S. & O’Brien, J. L. Silica-on-silicon waveguide quantum circuits. Science 320, 646–649 (2008).
Abrosimov, N. V. et al. A new generation of 99.999% enriched 28Si single crystals for the determination of Avogadro’s constant. Metrologia 54, 599–609 (2017).
Throckmorton, R. E., Barnes, E. & Das Sarma, S. Environmental noise effects on entanglement fidelity of exchange-coupled semiconductor spin qubits. Phys. Rev. B 95, 085405 (2017).
Martins, F. et al. Noise suppression using symmetric exchange gates in spin qubits. Phys. Rev. Lett. 116, 116801 (2016).
Wang, X. et al. Composite pulses for robust universal control of singlet–triplet qubits. Nat. Commun. 3, 997 (2012).
Horibe, K., Kodera, T. & Oda, S. Back-action-induced excitation of electrons in a silicon quantum dot with a single-electron transistor charge sensor. Appl. Phys. Lett. 106, 053119 (2015).
Shamim, S., Weber, B., Thompson, D. W., Simmons, M. Y. & Ghosh, A. Ultra low-noise atomic-scale structures for quantum circuitry in silicon. Nano Lett. 16, 5779–5784 (2016).
Keizer, J. G., Koelling, S., Koenraad, P. M. & Simmons, M. Y. Suppressing segregation in highly phosphorus doped silicon monolayers. ACS Nano 9, 12537–12541 (2015).
Gorman, S. K. et al. Tunneling statistics for analysis of spin-readout fidelity. Phys. Rev. Appl. 8, 034019 (2017).
Acknowledgements
The research was supported by the Australian Research Council Centre of Excellence for Quantum Computation and Communication Technology (project number CE170100012), the US Army Research Office under contract number W911NF-17-1-0202 and Silicon Quantum Computing Pty Ltd. M.Y.S. acknowledges an Australian Research Council Laureate Fellowship. This work was performed in part at the NSW node of the Australian National Fabrication Facility.
Reviewer information
Nature thanks Benjamin D’Anjou and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
Y.H., S.K.G. and L.K. fabricated the device. Y.H., S.K.G. and D.K. performed the measurements. Y.H., S.K.G., D.K, L.K. and J.G.K. analysed the data. The manuscript was written by Y.H., S.K.G. and M.Y.S. with input from all other authors. M.Y.S. conceived and supervised the project.
Corresponding author
Ethics declarations
Competing interests
M.Y.S. is a director of the company Silicon Quantum Computing Pty Ltd.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Determination of the number of donors in a qubit from the quantum dot charging energies.
a, RF-SET Coulomb diamonds. b, Gate–gate map around the (1, 3) ↔ (2, 2) charge transition and definitions of \({\rm{\delta }}{V}_{{\rm{g}}}^{{\rm{D}}{\rm{D}}}\), \({\rm{\Delta }}{V}_{{\rm{g}}}^{{\rm{S}}}\), \({\rm{\delta }}{V}_{{\rm{g}}}^{{\rm{S}}}\) and \({\rm{\delta }}{V}_{{\rm{g}}}^{{\rm{D}}}\). c, Gate–gate map for the regime with two electrons on donor qubits and definition of \({\rm{\Delta }}{V}_{{\rm{g}}}^{{\rm{D}}}\).
Extended Data Fig. 2 Experimental set-up for the two-qubit gate in a millikelvin dilution refrigerator.
The schematic shows the electrical connections from the device to the control computer at the different temperature stages of the dilution refrigerator from the top to bottom. An STM image of the device attached to the cold finger of the refrigerator at 50 mK is shown in the lower orange pane. The RF-reflectormetry circuit attached to the device employs a variable attenuator (‘Var. Atten.’) to control the power coupled through a directional coupler (‘Dir. Cplr.’) and sent to the source contact of the SET (red lines). The blue line is for d.c. current/voltage measurements of the SET. The slow signals (black components) and fast signals (green components) are combined using bias tees at 50 mK before being sent to the left and right gate electrodes.
Supplementary information
Supplementary Information
This file contains Supplementary Information Sections 1–5, Supplementary Tables 1–3, Supplementary References and Supplementary Figures 1–4.
Rights and permissions
About this article
Cite this article
He, Y., Gorman, S.K., Keith, D. et al. A two-qubit gate between phosphorus donor electrons in silicon. Nature 571, 371–375 (2019). https://doi.org/10.1038/s41586-019-1381-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1381-2
This article is cited by
-
High-fidelity initialization and control of electron and nuclear spins in a four-qubit register
Nature Nanotechnology (2024)
-
High-fidelity initialization and control of multiple nuclear spin qubits in silicon
Nature Nanotechnology (2024)
-
Compact terahertz harmonic generation in the Reststrahlenband using a graphene-embedded metallic split ring resonator array
Nature Communications (2024)
-
Atomic-scale manipulation of buried graphene–silicon carbide interface by local electric field
Communications Physics (2024)
-
A solid-state quantum microscope
Nature Electronics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.