Abstract
After two decades of development, cavity quantum electrodynamics with superconducting circuits has emerged as a rich platform for quantum computation and simulation. Lattices of coplanar waveguide resonators constitute artificial materials for microwave photons, in which interactions between photons can be incorporateded either through the use of nonlinear resonator materials or through coupling between qubits and resonators. Here we make use of the previously overlooked property that these lattice sites are deformable and permit tight-binding lattices that are unattainable even in solid-state systems. We show that networks of coplanar waveguide resonators can create a class of materials that constitute lattices in an effective hyperbolic space with constant negative curvature. We present numerical simulations of hyperbolic analogues of the kagome lattice that show unusual densities of states in which a macroscopic number of degenerate eigenstates comprise a spectrally isolated flat band. We present a proof-of-principle experimental realization of one such lattice. This paper represents a step towards on-chip quantum simulation of materials science and interacting particles in curved space.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
Data availability
The data and codes are available from the corresponding author upon reasonable request.
References
Cannon, J. W., Floyd, W. J., Kenyon, R. & Parry, W. R. in Flavors of Geometry 31, 59–115 (MSRI, 1997).
Leonhardt, U. & Philbin, T. G. General relativity in electrical engineering. New J. Phys. 8, 247 (2006).
Batz, S. & Peschel, U. Linear and nonlinear optics in curved space. Phys. Rev. A 78, 043821 (2008).
Smolyaninov, I. I. & Narimanov, E. E. Metric signature transitions in optical metamaterials. Phys. Rev. Lett. 105, 067402 (2010).
Genov, D. A., Zhang, S. & Zhang, X. Mimicking celestial mechanics in metamaterials. Nat. Phys. 5, 687–692 (2009).
Chen, H., Miao, R.-X. & Li, M. Transformation optics that mimics the system outside a Schwarzschild black hole. Opt. Express 18, 15183–15188 (2010).
Bekenstein, R. et al. Control of light by curved space in nanophotonic structures. Nat. Photon. 11, 664–670 (2017).
Bekenstein, R., Schley, R., Mutzafi, M., Rotschild, C. & Segev, M. Optical simulations of gravitational effects in the Newton–Schrödinger system. Nat. Phys. 11, 872–878 (2015).
Unruh, W. G. Experimental black-hole evaporation. Phys. Rev. Lett. 46, 1351–1353 (1981).
Weinfurtner, S., Tedford, E. W., Penrice, M. C. J., Unruh, W. G. & Lawrence, G. A. Measurement of stimulated Hawking emission in an analogue system. Phys. Rev. Lett. 106, 021302 (2011).
Philbin, T. G. et al. Fiber-optical analog of the event horizon. Science 319, 1367–1370 (2008).
Steinhauer, J. Observation of quantum Hawking radiation and its entanglement in an analogue black hole. Nat. Phys. 12, 959–965 (2016).
Carusotto, I., Fagnocchi, S., Recati, A., Balbinot, R. & Fabbri, A. Numerical observation of Hawking radiation from acoustic black holes in atomic Bose–Einstein condensates. New J. Phys. 10, 103001 (2008).
Gerace, D. & Carusotto, I. Analog Hawking radiation from an acoustic black hole in a flowing polariton superfluid. Phys. Rev. B 86, 144505 (2012).
Sabín, C. Mapping curved spacetimes into Dirac spinors. Sci. Rep. 7, 40346 (2017).
Pedernales, J. S. et al. Dirac equation in (1+1)-dimensional curved spacetime and the multiphoton quantum Rabi model. Phys. Rev. Lett. 120, 160403 (2018).
Koke, C., Noh, C. & Angelakis, D. G. Dirac equation in 2-dimensional curved spacetime, particle creation, and coupled waveguide arrays. Ann. Phys. 374, 162–178 (2016).
Boada, O., Celi, A., Latorre, J. I. & Lewenstein, M. Dirac equation for cold atoms in artificial curved spacetimes. New J. Phys. 13, 035002 (2011).
Houck, A. A., Türeci, H. E. & Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 8, 292–299 (2012).
Anderson, B. M., Ma, R., Owens, C., Schuster, D. I. & Simon, J. Engineering topological many-body materials in microwave cavity arrays. Phys. Rev. X 6, 041043 (2016).
Fitzpatrick, M., Sundaresan, N. M., Li, A. C. Y., Koch, J. & Houck, A. A. Observation of a dissipative phase transition in a one-dimensional circuit QED lattice. Phys. Rev. X 7, 011016 (2017).
Schmidt, S. & Koch, J. Circuit QED lattices: towards quantum simulation with superconducting circuits. Ann. Phys . (Berl.) 525, 395–412 (2013).
Underwood, D. L., Shanks, W. E., Koch, J. & Houck, A. A. Low-disorder microwave cavity lattices for quantum simulation with photons. Phys. Rev. A 86, 023837 (2012).
Coxeter, H. S. M. Regular honeycombs in hyperbolic space. In Proc. ICM Amsterdam 3, 155–169 (1954).
Schmidt, S., Gerace, D., Houck, A. A., Blatter, G. & Türeci, H. E. Nonequilibrium delocalization-localization transition of photons in circuit quantum electrodynamics. Phys. Rev. B 82, 100507 (2010).
Raftery, J., Sadri, D., Schmidt, S., Türeci, H. E. & Houck, A. A. Observation of a dissipation-induced classical to quantum transition. Phys. Rev. X 4, 031043 (2014).
Woess, W. Context-free languages and random walks on groups. Discrete Math. 67, 81–87 (1987).
Sunada, T. Group C∗-algebra sand the spectrum of a periodic Schrödinger operator on a manifold. Can. J. Math. 44, 180–193 (1992).
Floyd, W. J. & Plotnik, S. P. Growth functions on Fuchsian groups and the Euler characteristic. Invent. Math. 88, 1–29 (1987).
Bartholdi, L. & Ceccherini-Silberstein, T. G. Growth series and random walks on some hyperbolic graphs. Monatsh. Math. 136, 181–202 (2002).
Strichartz, R. S. Harmonic analysis as spectral theory of Laplacians. J. Funct. Anal. 87, 51–148 (1989).
McLaughlin, J. C. Random Walks and Convolution Operators on Free Products. PhD thesis, New York Univ. (1986).
Agmon, S. Spectral theory of Schrödinger operators on Euclidean and non-Euclidean spaces. Commun. Pure Appl. Math. 39, S3–S16 (1986).
Krioukov, D., Papadopoulos, F., Kitsak, M. & Vahdat, A. Hyperbolic geometry of complex networks. Phys. Rev. E 82, 036106 (2010).
Boguñá, M., Papadopoulos, F. & Krioukov, D. Sustaining the Internet with hyperbolic mapping. Nat. Commun. 1, 62 (2010).
Lipton, R. J. & Tarjan, R. E. A separator theorem for planar graphs. SIAM J. Appl. Math. 36, 177–189 (1979).
Breuckmann, N. P. & Terhal, B. M. Constructions and noise threshold of hyperbolic surface codes. IEEE Trans. Inf. Theory 62, 3731–3744 (2016).
Breuckmann, N. P., Vuillot, C., Campbell, E., Krishna, A. & Terhal, B. M. Hyperbolic and semi-hyperbolic surface codes for quantum storage. Quantum Sci. Technol. 2, 035007 (2017).
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).
Reagor, M. et al. Quantum memory with millisecond coherence in circuit QED. Phys. Rev. B 94, 014506 (2016).
Ashcroft, N. W. & Mermin, N. D. Solid State Physics (Thomson Learning, 1976).
Kroto, H. W., Heath, J. R., O’Brien, S. C., Curl, R. F. & Smalley, R. E. C60: buckminsterfullerene. Nature 318, 162–163 (1985).
Bergman, D. L., Wu, C. & Balents, L. Band touching from real-space topology in frustrated hopping models. Phys. Rev. B 78, 125104 (2008).
Leykam, D., Andreanov, A. & Flach, S. Artificial flat band systems: from lattice models to experiments. Adv. Phys. X 3, 1473052 (2018).
Kollár, A. J., Fitzpatrick, M., Sarnak, P. & Houck, A. A. Line-graph lattices: Euclidean and non-Euclidean flat bands, and implementations in circuit quantum electrodynamics. Preprint at https://arxiv.org/abs/1902.02794 (2019).
Annunziata, A. J. et al. Tunable superconducting nanoinductors. Nanotechnology 21, 445202 (2010).
Rotzinger, H. et al. Aluminium-oxide wires for superconducting high kinetic inductance circuits. Supercond. Sci. Technol. 30, 025002 (2016).
Kesten, H. Symmetric random walks on groups. Trans. Am. Math. Soc. 92, 336–354 (1959).
Chen, M. S., Onsager, L., Bonner, J. & Nagle, J. Hopping of ions in ice. J. Chem. Phys. 60, 405–419 (1974).
Carroll, S. M. Lecture notes on general relativity. Preprint at https://arxiv.org/abs/gr-qc/9712019 (1997).
Dunham, D., Lindgren, J. & Witte, D. Creating repeating hyperbolic patterns. Comput. Graph. 15, 215–223 (1981).
Adcock, B. M., Jones, K. C., Reiter, C. A. & Vislocky, L. M. Iterated function systems with symmetry in the hyperbolic plane. Comput. Graph. 24, 791–796 (2000).
Acknowledgements
We thank P. Sarnak, J. Kollár, R. Bekenstein, C. Fefferman and S. Parameswaran for discussions. This work was supported by the US National Science Foundation, the Princeton Center for Complex Materials (DMR-1420541) and the Multidisciplinary University Research Initiative (MURI) (W911NF-15-1-0397).
Author information
Authors and Affiliations
Contributions
A.J.K. conceived of the experiment, performed numerical simulations, measured the device and prepared the manuscript. M.F. designed, fabricated and measured the device, and prepared the manuscript. A.A.H. supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Reviewer information Nature thanks Göran Johansson, Prof. Enrique Solano and Martin Weides for their contribution to the peer review of this work.
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 System-size effects.
a, Numerical eigenenergy spectra for the heptagon-kagome lattice versus system size. The smallest layout tiling consists of a central heptagon and a shell of seven immediate neighbours (one shell). Each successive tiling includes another shell of immediate neighbours of the previous one. The spectra are plotted for one (red), two (blue), three (cyan) and four (gold) shells of neighbours. b–e, The results for each individual system size. The density of states converges rapidly with number of shells despite relatively small system sizes and effective hard-wall confinement. The theoretical plots elsewhere in this paper are from three-shell simulations. The experimental device consists of two shells.
Extended Data Fig. 2 Colour plots of selected numerical eigenstates of three shells of the heptagon-kagome lattice.
States are ordered from highest to lowest energy, and are plotted by placing a circle on each lattice site of the effective lattice. The size of the circle indicates the amplitude of the state on that site, and the colour its phase. a, The maximally excited state. This state is uniform in phase, but its amplitude varies radially owing to the effective confinement from the missing links at the boundary of the simulation. b, c, Examples of the two next-highest states. They bear a striking resemblance to Laguerre–Gaussian or particle-in-a-cylindrical-box modes found in flat Euclidean space. d–f, Selected intermediate excited states. Notice that the state in f shows both amplitude and phase modulation in the azimuthal direction, with independent periods. g, The localized eigenstate of compact support that forms the flat band.
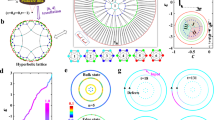
Extended Data Fig. 3 Poincaré-disk-model1,52,53 conformal projections of hyperbolic lattices.
a–d, Graphene-like lattices formed from heptagons, octagons, nonagons and dodecagons, respectively. e–h, The corresponding kagome-like effective lattices that arise when a–d are used as the layout lattice. i, A table of inter-site spacings for graphene-like hyperbolic layout lattices and their medial lattices, the kagome-like effective lattices. All distances are given in terms of the curvature length \(R=1/\sqrt{| K| }\). As the number of sides of the layout polygon increases, the intrinsic curvature of the tiling also grows, and the polygons become markedly larger.
Rights and permissions
About this article
Cite this article
Kollár, A.J., Fitzpatrick, M. & Houck, A.A. Hyperbolic lattices in circuit quantum electrodynamics. Nature 571, 45–50 (2019). https://doi.org/10.1038/s41586-019-1348-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1348-3
This article is cited by
-
Hyperbolic photonic topological insulators
Nature Communications (2024)
-
Cavity-mediated long-range interactions in levitated optomechanics
Nature Physics (2024)
-
Activating non-Hermitian skin modes by parity-time symmetry breaking
Communications Physics (2024)
-
Anomalous and Chern topological waves in hyperbolic networks
Nature Communications (2024)
-
On the Hyperbolic Bloch Transform
Annales Henri Poincaré (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.