Abstract
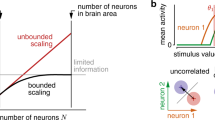
A neuronal population encodes information most efficiently when its stimulus responses are high-dimensional and uncorrelated, and most robustly when they are lower-dimensional and correlated. Here we analysed the dimensionality of the encoding of natural images by large populations of neurons in the visual cortex of awake mice. The evoked population activity was high-dimensional, and correlations obeyed an unexpected power law: the nth principal component variance scaled as 1/n. This scaling was not inherited from the power law spectrum of natural images, because it persisted after stimulus whitening. We proved mathematically that if the variance spectrum was to decay more slowly then the population code could not be smooth, allowing small changes in input to dominate population activity. The theory also predicts larger power-law exponents for lower-dimensional stimulus ensembles, which we validated experimentally. These results suggest that coding smoothness may represent a fundamental constraint that determines correlations in neural population codes.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All of the processed deconvolved calcium traces are available on figshare41 (https://figshare.com/articles/Recordings_of_ten_thousand_neurons_in_visual_cortex_in_response_to_2_800_natural_images/6845348), together with the image stimuli.
Code availability
The code is available on GitHub (https://github.com/MouseLand/stringer-pachitariu-et-al-2018b).
References
Barlow, H. B. in Sensory Communication (ed. Rosenblith, W.) 217–234 (MIT Press, 1961).
Atick, J. J. & Redlich, A. N. Towards a theory of early visual processing. Neural Comput. 2, 308–320 (1990).
Simoncelli, E. P. & Olshausen, B. A. Natural image statistics and neural representation. Annu. Rev. Neurosci. 24, 1193–1216 (2001).
DiCarlo, J. J., Zoccolan, D. & Rust, N. C. How does the brain solve visual object recognition? Neuron 73, 415–434 (2012).
Rigotti, M. et al. The importance of mixed selectivity in complex cognitive tasks. Nature 497, 585–590 (2013).
Chung, S., Lee, D. D. & Sompolinsky, H. Classification and geometry of general perceptual manifolds. Phys. Rev. X 8, 031003 (2018).
Cunningham, J. P. & Yu, B. M. Dimensionality reduction for large-scale neural recordings. Nat. Neurosci. 17, 1500–1509 (2014).
Machens, C. K., Romo, R. & Brody, C. D. Functional, but not anatomical, separation of “what” and “when” in prefrontal cortex. J. Neurosci. 30, 350–360 (2010).
Kobak, D. et al. Demixed principal component analysis of neural population data. eLife 5, e10989 (2016).
Archer, E. W., Koster, U., Pillow, J. W. & Macke, J. H. Low-dimensional models of neural population activity in sensory cortical circuits. In Proc. 27th International Conference on Neural Information Processing Systems (eds Ghahramani, Z. et al.) 343–351 (Curran, 2014).
Sadtler, P. T. et al. Neural constraints on learning. Nature 512, 423–426 (2014).
Chapin, J. K. & Nicolelis, M. A. Principal component analysis of neuronal ensemble activity reveals multidimensional somatosensory representations. J. Neurosci. Methods 94, 121–140 (1999).
Bathellier, B., Buhl, D. L., Accolla, R. & Carleton, A. Dynamic ensemble odor coding in the mammalian olfactory bulb: sensory information at different timescales. Neuron 57, 586–598 (2008).
Churchland, M. M. et al. Neural population dynamics during reaching. Nature 487, 51–56 (2012).
Mante, V., Sussillo, D., Shenoy, K. V. & Newsome, W. T. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature 503, 78–84 (2013).
Shadlen, M. N. & Newsome, W. T. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci. 18, 3870–3896 (1998).
Reich, D. S., Mechler, F. & Victor, J. D. Independent and redundant information in nearby cortical neurons. Science 294, 2566–2568 (2001).
Gao, P. et al. A theory of multineuronal dimensionality, dynamics and measurement. Preprint at https://www.biorxiv.org/content/early/2017/11/12/214262 (2017).
Pachitariu, M. et al. Suite2p: beyond 10,000 neurons with standard two-photon microscopy. Preprint at https://www.biorxiv.org/content/early/2017/07/20/061507 (2016).
Deng, J. et al. Imagenet: A large-scale hierarchical image database. In IEEE Conference on Computer Vision and Pattern Recognition 248–255 (IEEE, 2009).
Vinje, W. E. & Gallant, J. L. Natural stimulation of the nonclassical receptive field increases information transmission efficiency in V1. J. Neurosci. 22, 2904–2915 (2002).
Ringach, D. L. Spatial structure and symmetry of simple-cell receptive fields in macaque primary visual cortex. J. Neurophysiol. 88, 455–463 (2002).
Niell, C. M. & Stryker, M. P. Highly selective receptive fields in mouse visual cortex. J. Neurosci. 28, 7520–7536 (2008).
Softky, W. R. & Koch, C. The highly irregular firing of cortical cells is inconsistent with temporal integration of random EPSPs. J. Neurosci. 13, 334–350 (1993).
Cossell, L. et al. Functional organization of excitatory synaptic strength in primary visual cortex. Nature 518, 399–403 (2015).
Smyth, D., Willmore, B., Baker, G. E., Thompson, I. D. & Tolhurst, D. J. The receptive-field organization of simple cells in primary visual cortex of ferrets under natural scene stimulation. J. Neurosci. 23, 4746–4759 (2003).
Carandini, M. et al. Do we know what the early visual system does? J. Neurosci. 25, 10577–10597 (2005).
David, S. V. & Gallant, J. L. Predicting neuronal responses during natural vision. Netw. Comput. Neural Syst 16, 239–260 (2005).
Touryan, J., Felsen, G. & Dan, Y. Spatial structure of complex cell receptive fields measured with natural images. Neuron 45, 781–791 (2005).
de Vries, S. E. J. et al. A large-scale, standardized physiological survey reveals higher order coding throughout the mouse visual cortex. Preprint at https://www.biorxiv.org/content/early/2018/06/29/359513 (2018).
Field, D. J. Relations between the statistics of natural images and the response properties of cortical cells. J. Opt. Soc. Am. A 4, 2379–2394 (1987).
Ruderman, D. L. & Bialek, W. Statistics of natural images: Scaling in the woods. In Advances in Neural Information Processing Systems 551–558 (1994).
Tao, T. An Epsilon of Room, I: Real Analysis 1.12.3 (American Mathematical Society, 2010).
Szegedy, C. et al. Intriguing properties of neural networks. Preprint at http://arxiv.org/abs/1312.6199 (2013).
Goodfellow, I. J., Shlens, J. & Szegedy, C. Explaining and harnessing adversarial examples. Preprint at http://arxiv.org/abs/1412.6572 (2014).
Stringer, C. et al. Spontaneous behaviors drive multidimensional, brainwide activity. Science 364, eaav7893 (2019).
Pologruto, T. A., Sabatini, B. L. & Svoboda, K. ScanImage: flexible software for operating laser scanning microscopes. Biomed. Eng. Online 2, 13 (2003).
Chen, T.-W. et al. Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300 (2013).
Friedrich, J., Zhou, P. & Paninski, L. Fast online deconvolution of calcium imaging data. PLoS Comput. Biol. 13, e1005423 (2017).
Pachitariu, M., Stringer, C. & Harris, K. D. Robustness of spike deconvolution for neuronal calcium imaging. J. Neurosci. 38, 7976–7985 (2018).
Stringer, C., Pachitariu, M., Carandini, M. & Harris, K. Responses of ten thousand neurons to 2,800 natural images. Figshare https://doi.org/10.25378/janelia.6845348.v3 (2018).
Jun, J. J. et al. Fully integrated silicon probes for high-density recording of neural activity. Nature 551, 232–236 (2017).
Pachitariu, M., Steinmetz, N. A., Kadir, S. N., Carandini, M. & Harris, K. D. Fast and accurate spike sorting of high-channel count probes with kilosort. In Advances in Neural Information Processing Systems 4448–4456 (2016).
Allen, W. E. et al. Thirst regulates motivated behavior through modulation of brainwide neural population dynamics. Science 364, eaav3932(2019).
Izenman, A. J. Reduced-rank regression for the multivariate linear model. J. Multivariate Anal. 5, 248–264 (1975).
Schwartz, O. & Simoncelli, E. P. Natural signal statistics and sensory gain control. Nat. Neurosci. 4, 819–825 (2001).
Cowley, B. R., Smith, M. A., Kohn, A. & Yu, B. M. Stimulus-driven population activity patterns in macaque primary visual cortex. PLoS Comput. Biol. 12, e1005185 (2016).
Gallego, J. A. et al. Cortical population activity within a preserved neural manifold underlies multiple motor behaviors. Nat. Commun. 9, 4233 (2018).
Acknowledgements
We thank M. Krumin for assistance with the two-photon microscopes, C. Reddy for surgeries, and K. Falconer, A. Gretton and M. Benna for discussions of mathematics. This research was funded by Wellcome Trust Investigator grants (108726, 205093 and 204915) and by a grant from the Simons Foundation (SCGB 325512). C.S. was funded by a four-year Gatsby Foundation PhD studentship. M.C. holds the GlaxoSmithKline/Fight for Sight Chair in Visual Neuroscience. K.D.H. was funded by the European Research Council (694401). N.S. was supported by postdoctoral fellowships from the Human Frontier Sciences Program and the Marie Curie Action of the EU (656528). C.S. and M.P. are now funded by HHMI Janelia.
Reviewer information
Nature thanks Jakob Macke, Ken Miller and Byron Yu for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
C.S., M.P., N.S., M.C. and K.D.H. conceptualized the study; C.S., M.P., N.S. and K.D.H. devised the methodology; C.S. and M.P. designed the software; C.S., M.P. and N.S. performed experiments; C.S. and M.P. analysed the data; K.D.H. proved mathematical theorems; C.S., M.P., N.S., M.C. and K.D.H. wrote the paper; and M.C. and K.D.H. provided resources and acquired funding.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Reliability of single-neuron responses.
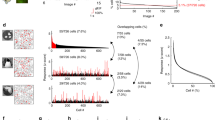
a, The responses of a single neuron to the first repeat of 2,800 stimuli plotted against its responses to the second repeat of the same stimuli. b, Histograms of P values for Pearson correlation of responses on the two repeats. Each coloured histogram represents a different recording. In total, 81.4 ± 5.1% (mean ± s.e.m., n = 7 recordings) of cells were significant at P < 0.05. c, Histogram of the single-neuron percentage of stimulus-related variance across the population. Each coloured histogram represents a different recording; arrowheads (top) represent the mean for each experiment.
Extended Data Fig. 2 Comparison with electrophysiology.
a, b, Single trial responses of 100 neurons to two repeats of 50 stimuli, recorded by two-photon calcium imaging. c, Distribution of tuning SNR for 74,353 neurons recorded by two-photon calcium imaging. d, Average peristimulus time histogram of spikes recorded electrophysiologically in a separate set of experiments. The images shown were a random subset of 700 images out of the total 2,800. The peristimulus time histogram reflects the average over all stimuli. The responses are z-scored across time for each neuron. e–g, Same as a–c for the electrophysiologically recorded neurons.
Extended Data Fig. 3 Single-neuron receptive fields estimated using reduced-rank regression and Gabor models.
a, The receptive fields of 159 randomly chosen neurons, estimated using reduced-rank regression. The receptive field map is z-scored for each neuron. b, An example Gabor fit to a single cell. c–h, Histograms showing the distribution of model parameters across cells. Each colour represents cells from one recording. i–n, Histograms showing the distribution of model parameters across cells when the model also has divisive normalization. o–u, Eigenspectra of Gabor population model responses to the different stimulus sets, as labelled. The unnormalized Gabors are shown in magenta, and the model with divisive normalization in black.
Extended Data Fig. 4 Stimulus-independent activity does not affect the measured eigenspectrum.
a, To measure the effects of correlated noise variability on eigenspectra estimated by cvPCA, we examined the effect of projecting out different numbers of noise dimensions (estimated during periods of spontaneous grey-screen) from the responses in an example experiment. b, The same analysis as in a, averaged over all recordings. The presence of these noise dimensions made little difference to the estimated signal eigenspectrum other than to slightly reduce estimated eigenvalues in the highest and lowest dimensions. For the main analyses, 32 spontaneous dimensions were subtracted.
Extended Data Fig. 5 Validating the eigenspectrum estimation method using simulations with the true noise distribution.
a, Scatterplots illustrating the noise levels of each estimated PC. Each plot shows population activity projected onto the specified PC, for the first repeat (x axis) and second repeat (y axis). Each point represents responses to a single stimulus. b, Estimated level of noise variance in successive signal dimensions. Noise variance was estimated by subtracting the cvPCA estimate of signal variance from the total variance (see Methods). c, Recovery of ground-truth eigenspectrum in simulated data. We simulated responses of 10,000 neurons to 2,800 stimuli with a power spectrum decay of exactly α = 1, and added noise in the stimulus space, generated with the spectrum in b scaled to produce the same signal-to-noise ratio as in the original neural data. The ground-truth eigenspectrum (black) is estimated accurately by the cvPCA method (blue). d, Same analysis as in c with multiplicative noise, in which the responses of all neurons on each trial were multiplied by a common random factor. The distribution of this factor was again scaled to recover the original signal-to-noise ratio. e, Same analysis as in c with a combination of multiplicative and additive noise. f, Same analysis as in c, also including simulation of neural and two-photon shot noise before running a GCaMP deconvolution algorithm. g, Ten instantiations of the simulation were performed with ground-truth exponents of 0.5, 1.0 and 1.5. Error bars represent standard deviations of the power-law exponents estimated for each of the ten simulations. The dashed black line represents the ground-truth value. h–j, Comparison of cvPCA (yellow) and traditional PCA (green) algorithms in the presence of the additive + multiplicative noise combination. Whereas cvPCA recovered the ground-truth eigenspectrum (black) exactly, traditional PCA did not, resulting in overestimation of the top eigenvalues and failure to detect the ground-truth power law.
Extended Data Fig. 6 Successive PC dimensions encode finer stimulus features.
Each plot shows the responses of 10,145 neurons to 2,800 natural images, projected onto the specified PCs and then sorted along both axes so that correlated neurons and stimuli are close together. We then smoothed the matrix across neurons and stimuli with Gaussian kernels of widths of 8 neurons and 2 stimuli, respectively. Dimensions 1–2 reveal a coarse, one-dimensional organization of the neurons and stimuli. Dimensions 3–10 reveal multidimensional structure, which involves different neural subpopulations responding to different stimuli. Dimensions 11–40 reveal finer-structured patterns of correlated selectivity among neurons. Dimensions 41–200 and 201–1,000 reveal even finer-structured selectivity, which contained less neural variance.
Extended Data Fig. 7 Power-law scaling reflects correlation structure, not single-neuron statistics.
a, The signal variance of the responses of each neuron are sorted in descending order; they approximately follow a power law with a decay exponent of α = 0.59. b, The same plot after z-scoring the recorded traces to equalize stimulus response sizes between cells; the distribution of single-neuron variance has become nearly flat. c, PC eigenspectra for z-scored data. Each coloured line represents a different recording. The dashed blue line shows the average eigenspectrum from the original, non-z-scored responses. The fact that the eigenspectrum power law is barely affected by equalizing firing rates, whereas the distribution of single-cell signal variance is altered, indicates that the power law arises from correlations between cells rather than from the distribution of firing rates or signal variance across cells.
Extended Data Fig. 8 Power-law eigenspectra in concatenated recordings.
a–c, To investigate whether power-law eigenspectra apply to even larger populations, we were able to artificially double the number of recorded neurons by combining three pairs of recordings for which the imaging fields of view had similar retinotopic locations. Top, retinotopic locations of receptive fields (95% confidence intervals on the mean receptive field position of that recording), with each recording shown in a different shade of blue. Bottom, eigenspectrum of concatenated recordings in response to the 2,800 natural image stimuli; total population sizes 19,571, 23,472 and 18,807 cells respectively. Each panel (a, b and c) represents one pair of recordings. d, Eigenspectrum exponents for random subsets of the combined populations (compare with Fig. 2j). The horizontal axis shows the population size relative to single recordings, so the merged population has size 2. The mean power-law exponent for fraction of neurons = 2 was α = 0.99 ± 0.02 (mean ± s.e.m.).
Extended Data Fig. 9 Eigenspectrum of electrophysiologically recorded data.
We recorded neural activity electrophysiologically in response to 700 out of the 2,800 stimuli, and concatenated the recordings, resulting in a total of 877 neurons recorded across 6 experiments. a, With this smaller number of stimuli and neurons, convergence to a power law is not complete, and the exponent cannot be estimated accurately (compare with Fig. 2g–j). We therefore compared the electrophysiology data to the responses generated by these stimuli in 877 neurons sampled randomly from either a single two-photon imaging experiment (dark blue) or all experiments combined (light blue). The red and pink colours show electrophysiology eigenspectra with time bins of 50 ms or 500 ms; the red line shows the best linear fit to estimate the exponent. b, The blue curves represent power-law exponents estimated from the responses of different-sized neuronal subpopulations to this set of 700 stimuli; the shading represents s.e.m. over different random subsets of neurons. The red and pink crosses denote estimated exponents from electrophysiology data for 50-ms and 500-ms bin sizes.
Extended Data Fig. 10 Power-law scaling grows more accurate for increasing numbers of neurons and stimuli, for all stimulus ensembles.
a, Eigenspectra estimated from a random subset of the recorded neurons, colour-coded by the fraction of neurons retained. b, Eigenspectra estimated from a random subset of stimuli, colour-coded by the fraction of stimuli retained. c, Correlation coefficient of the spectra plotted in a, b. d, Power-law exponent of the spectra plotted in a, b. Each row corresponds to a different ensemble of visual stimuli.
Supplementary information
Supplementary Information
This file contains the Supplementary Discussion.
Rights and permissions
About this article
Cite this article
Stringer, C., Pachitariu, M., Steinmetz, N. et al. High-dimensional geometry of population responses in visual cortex. Nature 571, 361–365 (2019). https://doi.org/10.1038/s41586-019-1346-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1346-5
This article is cited by
-
Local origin of excitatory–inhibitory tuning equivalence in a cortical network
Nature Neuroscience (2024)
-
Minute-scale oscillatory sequences in medial entorhinal cortex
Nature (2024)
-
Neuronal travelling waves explain rotational dynamics in experimental datasets and modelling
Scientific Reports (2024)
-
High-density transparent graphene arrays for predicting cellular calcium activity at depth from surface potential recordings
Nature Nanotechnology (2024)
-
Heavy-tailed neuronal connectivity arises from Hebbian self-organization
Nature Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.