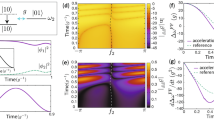
Abstract
In quantum physics, measurements can fundamentally yield discrete and random results. Emblematic of this feature is Bohr’s 1913 proposal of quantum jumps between two discrete energy levels of an atom1. Experimentally, quantum jumps were first observed in an atomic ion driven by a weak deterministic force while under strong continuous energy measurement2,3,4. The times at which the discontinuous jump transitions occur are reputed to be fundamentally unpredictable. Despite the non-deterministic character of quantum physics, is it possible to know if a quantum jump is about to occur? Here we answer this question affirmatively: we experimentally demonstrate that the jump from the ground state to an excited state of a superconducting artificial three-level atom can be tracked as it follows a predictable ‘flight’, by monitoring the population of an auxiliary energy level coupled to the ground state. The experimental results demonstrate that the evolution of each completed jump is continuous, coherent and deterministic. We exploit these features, using real-time monitoring and feedback, to catch and reverse quantum jumps mid-flight—thus deterministically preventing their completion. Our findings, which agree with theoretical predictions essentially without adjustable parameters, support the modern quantum trajectory theory5,6,7,8,9 and should provide new ground for the exploration of real-time intervention techniques in the control of quantum systems, such as the early detection of error syndromes in quantum error correction.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
References
Bohr, N. On the constitution of atoms and molecules. Part I. Binding of electrons by positive nuclei. Phil. Mag. 26, 1–25 (1913).
Nagourney, W., Sandberg, J. & Dehmelt, H. Shelved optical electron amplifier: observation of quantum jumps. Phys. Rev. Lett. 56, 2797–2799 (1986).
Sauter, T., Neuhauser, W., Blatt, R. & Toschek, P. E. Observation of quantum jumps. Phys. Rev. Lett. 57, 1696 (1986).
Bergquist, J. C., Hulet, R. G., Itano, W. M. & Wineland, D. J. Observation of quantum jumps in a single atom. Phys. Rev. Lett. 57, 1699–1702 (1986).
Carmichael, H. J. An Open Systems Approach to Quantum Optics (Springer, 1993).
Gardiner, C. W., Parkins, A. S. & Zoller, P. Wave-function quantum stochastic differential equations and quantum-jump simulation methods. Phys. Rev. A 46, 4363–4381 (1992).
Dalibard, J., Castin, Y. & Mølmer, K. Wave-function approach to dissipative processes in quantum optics. Phys. Rev. Lett. 68, 580–583 (1992).
Plenio, M. B. & Knight, P. L. The quantum-jump approach to dissipative dynamics in quantum optics. Rev. Mod. Phys. 70, 101–144 (1998).
Korotkov, A. N. Continuous quantum measurement of a double dot. Phys. Rev. B 60, 5737–5742 (1999).
Einstein, A. Strahlungs-emission und -absorption nach der Quantentheorie. Verh. Deutsch. Phys. Ges. 18, 318–323 (1916).
Einstein, A. Quantentheorie der Strahlung. Phys. Z. 18, 121–128 (1917).
Schrödinger, E. Are there quantum jumps? Br. J. Phil. Sci. 3, 109–123; 233–242 (1952).
Basché, T., Kummer, S. & Brauchle, C. Direct spectroscopic observation of quantum jumps of a single molecule. Nature 373, 132–134 (1995).
Peil, S. & Gabrielse, G. Observing the quantum limit of an electron cyclotron: QND measurements of quantum jumps between Fock states. Phys. Rev. Lett. 83, 1287–1290 (1999).
Gleyzes, S. S. et al. Quantum jumps of light recording the birth and death of a photon in a cavity. Nature 446, 297–300 (2007).
Guerlin, C. et al. Progressive field-state collapse and quantum non-demolition photon counting. Nature 448, 889–893 (2007).
Jelezko, F. et al. Single spin states in a defect center resolved by optical spectroscopy. Appl. Phys. Lett. 81, 2160 (2002).
Neumann, P. et al. Single-shot readout of a single nuclear spin. Science 329, 542–544 (2010).
Robledo, L. et al. High fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Vijay, R., Slichter, D. H. & Siddiqi, I. Observation of quantum jumps in a superconducting artificial atom. Phys. Rev. Lett. 106, 110502 (2011).
Hatridge, M. et al. Quantum back-action of an individual variable-strength measurement. Science 339, 178–181 (2013).
Deléglise, S. et al. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514 (2008).
Sayrin, C. et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 477, 73–77 (2011).
Sun, L. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444–448 (2014).
Ofek, N. et al. Demonstrating quantum error correction that extends the lifetime of quantum information. Nature 536, 441–445 (2016).
Porrati, M. & Putterman, S. Wave-function collapse due to null measurements: the origin of intermittent atomic fluorescence. Phys. Rev. A 36, 929–932 (1987).
Mabuchi, H. & Zoller, P. Inversion of quantum jumps in quantum optical systems under continuous observation. Phys. Rev. Lett. 76, 3108–3111 (1996).
Ruskov, R., Mizel, A. & Korotkov, A. N. Crossover of phase qubit dynamics in the presence of a negative-result weak measurement. Phys. Rev. B 75, 220501 (2007).
Volz, J., Gehr, R., Dubois, G., Esteve, J. & Reichel, J. Measurement of the internal state of a single atom without energy exchange. Nature 475, 210–213 (2011).
Ristè, D. et al. Deterministic entanglement of superconducting qubits by parity measurement and feedback. Nature 502, 350–354 (2013).
Murch, K. W., Weber, S. J., Beck, K. M., Ginossar, E. & Siddiqi, I. Reduction of the radiative decay of atomic coherence in squeezed vacuum. Nature 499, 62–65 (2013).
Weber, S. J. et al. Mapping the optimal route between two quantum states. Nature 511, 570–573 (2014).
Katz, N. et al. Coherent state evolution in a superconducting qubit from partial-collapse measurement. Science 312, 1498–1500 (2006).
Cook, R. J. What are quantum jumps? Phys. Scr. 1988, 49 (1988).
Bergeal, N. et al. Phase-preserving amplification near the quantum limit with a Josephson ring modulator. Nature 465, 64–68 (2010).
Minev, Z. et al. Planar multilayer circuit quantum electrodynamics. Phys. Rev. Appl. 5, 044021 (2016).
Lecocq, F. et al. Junction fabrication by shadow evaporation without a suspended bridge. Nanotechnology 22, 315302 (2011).
Rigetti, C. T. Quantum Gates for Superconducting Qubits. PhD thesis, Yale Univ. (2009).
Minev, Z. K. Catching and Reversing a Quantum Jump Mid-Flight. PhD thesis, Yale Univ. (2019).
Chow, J. M. et al. Optimized driving of superconducting artificial atoms for improved single-qubit gates. Phys. Rev. A 82, 040305 (2010).
Reed, M. D. Entanglement and Quantum Error Correction with Superconducting Qubits. PhD thesis, Yale Univ. (2013).
Bylander, J. et al. Noise spectroscopy through dynamical decoupling with a superconducting flux qubit. Nat. Phys. 7, 565–570 (2011).
Eichler, C. et al. Observation of entanglement between itinerant microwave photons and a superconducting qubit. Phys. Rev. Lett. 109, 240501 (2012).
Liu, Y. Quantum Feedback Control of Multiple Superconducting Qubits. PhD thesis, Yale Univ. (2016).
Ristè, D., Bultink, C. C., Lehnert, K. W. & DiCarlo, L. Feedback control of a solid-state qubit using high-fidelity projective measurement. Phys. Rev. Lett. 109, 240502 (2012).
Acknowledgements
Z.K.M. and M.H.D. acknowledge discussion with V. V. Albert, R. Blatt, S. M. Girvin, S. Korotkov, K. Mølmer, N. Ofek, W. D. Phillips, M. P. Silveri and H. M. Wiseman. V. V. Albert addressed one aspect of the Lindblad theoretical modelling regarding the waiting time. Use of facilities was supported by the Yale Institute for Nanoscience and Quantum Engineering (YINQE), the Yale SEAS cleanroom and the US National Science Foundation MRSEC DMR 1119826. This research was supported by Army Research Office under grant number W911NF-14-1-0011. R.G.-J. and H.J.C. acknowledge the support of the Marsden Fund Council from government funding, administered by the Royal Society of New Zealand under contract number UOA1328.
Author information
Authors and Affiliations
Contributions
Z.K.M. initiated, designed and performed the experiment, designed the sample, analysed the data and carried out the initial theoretical and numerical modelling of the experiment. Z.K.M. conceived the experiment based on theoretical predictions by H.J.C. H.J.C. and R.G.-J. performed the presented theoretical modelling and numerical simulations. S.O.M. contributed to the experimental set-up and design of the device. S.O.M. and S.S. contributed to the fabrication of the device. P.R. and R.J.S. assisted with the FPGA. M.M. contributed theoretical support. M.H.D. supervised the project. Z.K.M. and M.H.D. wrote the manuscript. H.J.C. contributed the theoretical supplement. All authors provided suggestions for the experiment, discussed the results and contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
R.J.S. and M.H.D. are founders, and R.J.S. is an equity shareholder, of Quantum Circuits, Inc.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Waiting time to switch from a |B〉 to not-|B〉 state assignment result.
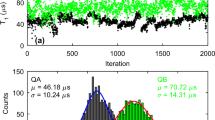
Semi-log plot of the histogram (shaded green) of the duration of times corresponding to |B〉-measurement results, τB, for 3.2 s of continuous data of the type shown in Fig. 2a. Solid line is an exponential fit which yields a 4.2 ± 0.03 μs time constant.
Extended Data Fig. 2 Mid-flight tomogram.
a, b, The plots show the real (a) and imaginary (b) parts of the conditional density matrix, ρc, at the mid-flight of the quantum jump (Δtcatch = Δtmid), in the presence of the Rabi drive from |G〉 to |D〉 (Δtoff = 0). The population of the |B〉 state is 0.023, and the magnitude of all imaginary components is less than 0.007.
Extended Data Fig. 3 Reversing the quantum jump mid-flight in the absence of ΩDG.
Success probabilities PG (purple) and PD (orange) to reverse to |G〉 and complete to |D〉 the quantum jump mid-flight at \({\rm{\Delta }}{t}_{{\rm{catch}}}={\rm{\Delta }}{t}_{{\rm{mid}}}^{^{\prime} }\), defined in Fig. 3b, in the absence of the Rabi drive ΩDG, where Δton = 2 μs and θI = π/2. The error bars are smaller than the size of the dots. In the presence of ΩDG, PG is 5% larger owing to a smaller T2 effect. Black dots denote the success probability for |G〉 (closed dots) and |D〉 (open dots) for the control experiment in which the intervention is applied at random times (see Fig. 4b).
Extended Data Fig. 4 Control flow of the experiment.
a, Flowchart illustrating the control flow of the catch and reverse experiments, whose results are shown in Figs. 3, 4. See Methods for the description of each block. b, Flowchart of the master and demodulator modules chiefly involved in the ‘monitor and catch Δton’ routine. The modules execute concurrently and share data synchronously, as discussed in Methods. c, Flowchart of the processing involved in the master module of the ‘monitor and catch Δtoff’ routine; see Methods.
Supplementary information
Supplementary Information
The file, which contains 5 figures and 3 tables, describes the theoretical modeling of the experiment, explicates the theoretical calculations involved in the analysis of the trajectory jump dynamics, and presents further control experiments and details on the results.
Rights and permissions
About this article
Cite this article
Minev, Z., Mundhada, S., Shankar, S. et al. To catch and reverse a quantum jump mid-flight. Nature 570, 200–204 (2019). https://doi.org/10.1038/s41586-019-1287-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1287-z
This article is cited by
-
Time-series quantum reservoir computing with weak and projective measurements
npj Quantum Information (2023)
-
Cloaking a qubit in a cavity
Nature Communications (2023)
-
Turing instability in quantum activator–inhibitor systems
Scientific Reports (2022)
-
Measurement-induced quantum phases realized in a trapped-ion quantum computer
Nature Physics (2022)
-
Experimental demonstration of continuous quantum error correction
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.