Abstract
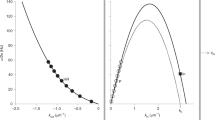
The entropy of a black hole1 and Hawking radiation2 should have the same temperature given by the surface gravity, within a numerical factor of the order of unity. In addition, Hawking radiation should have a thermal spectrum, which creates an information paradox3,4. However, the thermality should be limited by greybody factors5, at the very least6. It has been proposed that the physics of Hawking radiation could be verified in an analogue system7, an idea that has been carefully studied and developed theoretically8,9,10,11,12,13,14,15,16,17,18. Classical white-hole analogues have been investigated experimentally19,20,21, and other analogue systems have been presented22,23. The theoretical works and our long-term study of this subject15,24,25,26,27 enabled us to observe spontaneous Hawking radiation in an analogue black hole28. The observed correlation spectrum showed thermality at the lowest and highest energies, but the overall spectrum was not of the thermal form, and no temperature could be ascribed to it. Theoretical studies of our observation made predictions about the thermality and Hawking temperature29,30,31,32,33. Here we construct an analogue black hole with improvements compared with our previous setup, such as reduced magnetic field noise, enhanced mechanical and thermal stability and redesigned optics. We find that the correlation spectrum of Hawking radiation agrees well with a thermal spectrum, and its temperature is given by the surface gravity, confirming the predictions of Hawking’s theory. The Hawking radiation observed is in the regime of linear dispersion, in analogy with a real black hole, and the radiation inside the black hole is composed of negative-energy partner modes only, as predicted.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Bekenstein, J. D. Black holes and entropy. Phys. Rev. D 7, 2333–2346 (1973).
Hawking, S. W. Black hole explosions? Nature 248, 30–31 (1974).
Hawking, S. W. Breakdown of predictability in gravitational collapse. Phys. Rev. D 14, 2460–2473 (1976).
Wald, R. M. On particle creation by black holes. Commun. Math. Phys. 45, 9–34 (1975).
Page, D. N. Particle emission rates from a black hole: massless particles from an uncharged, nonrotating hole. Phys. Rev. D 13, 198–206 (1976).
Visser, M. Thermality of the Hawking flux. J. High Energy Phys. http://doi.org/10/1007/JHEP7(2015)009 (2015).
Unruh, W. G. Experimental black-hole evaporation? Phys. Rev. Lett. 46, 1351–1353 (1981).
Garay, L. J., Anglin, J. R., Cirac, J. I. & Zoller, P. Sonic analog of gravitational black holes in Bose–Einstein condensates. Phys. Rev. Lett. 85, 4643–4647 (2000).
Visser, M. Acoustic black holes: horizons, ergospheres and Hawking radiation. Class. Quantum Gravity 15, 1767–1791 (1998).
Balbinot, R., Fabbri, A., Fagnocchi, S., Recati, A. & Carusotto, I. Nonlocal density correlations as a signature of Hawking radiation from acoustic black holes. Phys. Rev. A 78, 021603 (2008).
Carusotto, I., Fagnocchi, S., Recati, A., Balbinot, R. & Fabbri, A. Numerical observation of Hawking radiation from acoustic black holes in atomic Bose–Einstein condensates. New J. Phys. 10, 103001 (2008).
Macher, J. & Parentani, R. Black-hole radiation in Bose–Einstein condensates. Phys. Rev. A 80, 043601 (2009).
Larré, P.-É., Recati, A., Carusotto, I. & Pavloff, N. Quantum fluctuations around black hole horizons in Bose–Einstein condensates. Phys. Rev. A 85, 013621 (2012).
Recati, A., Pavloff, N. & Carusotto, I. Bogoliubov theory of acoustic Hawking radiation in Bose–Einstein condensates. Phys. Rev. A 80, 043603 (2009).
Steinhauer, J. Measuring the entanglement of analogue Hawking radiation by the density–density correlation function. Phys. Rev. D 92, 024043 (2015).
Jacobson, T. A. & Volovik, G. E. Event horizons and ergoregions in 3He. Phys. Rev. D 58, 064021 (1998).
Schützhold, R. & Unruh, W. G. Hawking radiation in an electromagnetic waveguide? Phys. Rev. Lett. 95, 031301 (2005).
de Nova, J. R. M., Guéry-Odelin, D., Sols, F. & Zapata, I. Birth of a quasi-stationary black hole in an outcoupled Bose–Einstein condensate. New J. Phys. 16, 123033 (2014).
Weinfurtner, S., Tedford, E. W., Penrice, M. C. J., Unruh, W. G. & Lawrence, G. A. Measurement of stimulated Hawking emission in an analogue system. Phys. Rev. Lett. 106, 021302 (2011).
Rousseaux, G., Mathis, C., Maïssa, P., Philbin, T. G. & Leonhardt, U. Observation of negative-frequency waves in a water tank: a classical analogue to the Hawking effect? New J. Phys. 10, 053015 (2008).
Euvé, L.-P., Michel, F., Parentani, R., Philbin, T. G. & Rousseaux, G. Observation of noise correlated by the Hawking effect in a water tank. Phys. Rev. Lett. 117, 121301 (2016).
Philbin, T. G. et al. Fiber-optical analog of the event horizon. Science 319, 1367–1370 (2008).
Nguyen, H. S. et al. Acoustic black hole in a stationary hydrodynamic flow of microcavity polaritons. Phys. Rev. Lett. 114, 036402 (2015).
Lahav, O. et al. Realization of a sonic black hole analog in a Bose–Einstein condensate. Phys. Rev. Lett. 105, 240401 (2010).
Shammass, I., Rinott, S., Berkovitz, A., Schley, R. & Steinhauer, J. Phonon dispersion relation of an atomic Bose–Einstein condensate. Phys. Rev. Lett. 109, 195301 (2012).
Schley, R. et al. Planck distribution of phonons in a Bose–Einstein condensate. Phys. Rev. Lett. 111, 055301 (2013).
Steinhauer, J. Observation of self-amplifying Hawking radiation in an analogue black-hole laser. Nat. Phys. 10, 864–869 (2014).
Steinhauer, J. Observation of quantum Hawking radiation and its entanglement in an analogue black hole. Nat. Phys. 12, 959–965 (2016).
Michel, F., Coupechoux, J.-F. & Parentani, R. Phonon spectrum and correlations in a transonic flow of an atomic Bose gas. Phys. Rev. D 94, 084027 (2016).
Coutant, A. & Weinfurtner, S. Low-frequency analogue Hawking radiation: the Bogoliubov–de Gennes model. Phys. Rev. D 97, 025006 (2018).
Fabbri, A. & Pavloff, N. Momentum correlations as signature of sonic Hawking radiation in Bose–Einstein condensates. SciPost Phys. 4, 019 (2018).
Carusotto, I. & Balbinot, R. Acoustic Hawking radiation. Nat. Phys. 12, 897–898 (2016).
Robertson, S., Michel, F. & Parentani, R. Assessing degrees of entanglement of phonon states in atomic Bose gases through the measurement of commuting observables. Phys. Rev. D 96, 045012 (2017).
Salasnich, L., Parola, A. & Reatto, L. Dimensional reduction in Bose–Einstein-condensed alkali-metal vapors. Phys. Rev. A 69, 045601 (2004).
Steinhauer, J. et al. Bragg spectroscopy of the multibranch Bogoliubov spectrum of elongated Bose–Einstein condensates. Phys. Rev. Lett. 90, 060404 (2003).
Tozzo, C. & Dalfovo, F. Bogoliubov spectrum and Bragg spectroscopy of elongated Bose–Einstein condensates. New J. Phys. 5, 54 (2003).
Acknowledgements
We thank the participants of the LITP Analogue Gravity Workshop for their conversations. We thank I. Carusotto, R. Parentani, D. Marolf and F. Michel for comments. This work was supported by the Israel Science Foundation.
Author information
Authors and Affiliations
Contributions
J.R.M.d.N. and J.S. designed and built the experimental apparatus. J.R.M.d.N., K.G. and V.I.K. performed theoretical calculations. J.S. acquired the data. K.G., V.I.K. and J.S. analysed the data. J.R.M.d.N. performed the numerical simulations. J.R.M.d.N. and J.S. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Supplementary Figure 1.
Rights and permissions
About this article
Cite this article
Muñoz de Nova, J.R., Golubkov, K., Kolobov, V.I. et al. Observation of thermal Hawking radiation and its temperature in an analogue black hole. Nature 569, 688–691 (2019). https://doi.org/10.1038/s41586-019-1241-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1241-0
This article is cited by
-
Mesoscopic Klein-Schwinger effect in graphene
Nature Physics (2023)
-
Quantum simulation of Hawking radiation and curved spacetime with a superconducting on-chip black hole
Nature Communications (2023)
-
Low-dimensional quantum gases in curved geometries
Nature Reviews Physics (2023)
-
Analogue simulations of quantum gravity with fluids
Nature Reviews Physics (2023)
-
Higgs phonon: conformal phonon and Hawking temperature in a two-dimensional acoustic black hole model
General Relativity and Gravitation (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.