Abstract
In 2015, almost a century after Einstein published the general theory of relativity, one of its most important predictions was verified by direct detection: the production of gravitational waves in spacetime by accelerating objects. Since then, gravitational-wave astronomy has enabled tests of the nature of gravity and the properties of black holes, and in 2017 electromagnetic observations of a double neutron star merger producing gravitational waves led to a focus on multi-messenger astronomy. Here we review the history and accomplishments of gravitational-wave astronomy and look towards the future.
Similar content being viewed by others
Main
In his ‘miracle year’ of 1905, Albert Einstein demonstrated that atoms exist, showed that light comes in discrete packets and proved by elegant arguments that space and time are not absolute1,2,3,4. All of these ideas were to have a profound influence on the development of physics, but here we focus on his recasting of our understanding of space and time.

Using thought experiments, Einstein argued that the flow of time and the measurement of length have to depend on the relative state of motion of the observer if the speed of light in a vacuum is to be the same for all observers. His special theory of relativity therefore amended Newton’s classical mechanics through the introduction of a new four-dimensional continuum, a flexible spacetime. However, a new insight was required to describe gravity.
Einstein reasoned that in a vacuum, a freely falling body would experience no force at all, and as a result gravity had to be equivalent to acceleration5. This ‘happy’ thought would eventually develop into what we call the principle of equivalence. This founding block of his general theory of relativity would inexorably lead him to the conclusion that gravity has to be a manifestation of the curvature of spacetime.
Einstein’s general theory of relativity was published in its final form on 25 November 1915. Despite the theory’s mathematical elegance, Einstein’s eminence and the theory’s ability to explain the anomalous precession of Mercury’s orbit6, acceptance was initially slow owing to the lack of clear experimental evidence. A golden opportunity arose on 29 May 1919, when total-solar-eclipse measurements from the island of Príncipe in the Gulf of Guinea and from Sobral, Brazil allowed scientists to measure the deflection of light by gravity; critically, the general-relativistic prediction of 1.7 arcsec was double the deflection predicted using Newtonian gravity. The observations were of relatively poor quality but the agreement with the predictions of the general theory of relativity7 made Einstein a celebrity overnight. A much-less-heralded set of observations of the solar eclipse of 22 September 1922 were of outstanding quality and their precise agreement with the general theory of relativity quelled any remaining doubts about the correctness of the prediction8. Additional tests followed, first with the observation of gravitational redshifts5 in astronomical measurements in 19549 and in the laboratory in 195910, and later with the observation of gravitational time delay in 196411.
Have then all of the consequences of Einstein’s theory been tested? The answer is a clear no, as we shall see later in this article, but within the set of tests that have been performed, Einstein’s theory has passed with flying colours. The latest, and perhaps most dramatic, example is the recent detection of gravitational waves12. As early as 1916, Einstein predicted that if spacetime could curve in the presence of matter, then it could also undulate if matter accelerated13. Unfortunately, the first paper that he wrote on the subject had mathematical errors that were only corrected in 191814. More importantly, in 1922 Eddington studied Einstein’s paper and pointed out—in addition to another mathematical mistake—that some of the wave solutions that Einstein had obtained could have speeds higher than that of light; he wrote in his paper the dismissive remark that “the only speed of propagation relevant to them is the speed of thought”15. Such solutions are now understood to be artefacts of the coordinate system that Einstein used, and have no physical meaning. But back then, Eddington’s comment cast doubt on the nature of gravitational waves, which Einstein and his assistant Nathan Rosen would only make worse in subsequent years.
It would take another 35 years for these issues to be fully settled. An important argument came in 1957 at one of the first conferences on the general theory of relativity16, when British graduate student Felix Pirani showed precisely how waves could affect material particles. Another important argument came from Richard Feynman, who used a ‘sticky-beads’ thought experiment to argue that gravitational waves had to be real because they had to carry energy—a concept that was later proven by Pirani’s adviser, Hermann Bondi. At this same meeting, John Wheeler and Joe Weber argued that these waves might be physically measurable17.
If you build it, they will come
The ultimate proof that gravitational waves are real was their direct detection, but their first detection was indirect and relied on serendipity: the discovery of binary pulsars. In late 1967, radio pulses were discovered from rotating neutron stars18,19. These ‘pulsars’ are the best natural clocks in the Universe, which motivated Joseph Taylor to think about the measurements that could be made if a pulsar were to be detected in a binary system. The orbital properties of binaries are important because, according to Einstein’s theory, gravitational waves carry energy away from the binary, forcing it to decay20,21, and so the measurement of orbital-period decay would demonstrate that gravitational waves exist. Indeed in 1974, Taylor and his graduate student Russell Hulse discovered the first binary pulsar22 and received the 1993 Nobel Prize in Physics for their discovery. In 1981, orbital-period decay was measured in that system23, with a magnitude exactly in line with Einstein’s theory, to within a tiny observational uncertainty.
Although binary pulsars provided spectacular confirmation that gravitational waves exist, direct detection of gravitational waves was far more elusive. The first such attempts were made by Joe Weber at the University of Maryland, who determined after careful thought and experimentation that there were two designs of ground-based detectors that might be successful: resonant detectors and laser interferometers. Settling on the first, as more practical on a limited budget, in 1965 Weber built such a detector: a 1.5-tonne, 1 m × 2 m cylindrical bar made of solid aluminium that would resonate at a particular set of frequencies if excited by a gravitational wave.
The idea was the following. If a gravitational wave went through such a ‘Weber bar’, the undulations of spacetime would squeeze and stretch the bar, causing vibrations that—if forced at the resonance frequency of the bar—would produce measurable excitations. In 1969, Weber announced that he had detected gravitational waves in two bars separated by 1,000 km, one in Chicago and one in Maryland24. Unfortunately, these results could not be reproduced by other experimental groups, his data analysis methods were found not to be robust and the strength of the claimed signals was orders of magnitude greater than would be realistic for astrophysical sources. As a result, the physics community today does not believe that the signals were detections of gravitational waves.
Nevertheless, Weber’s experimental work and techniques, together with his unverified announcement, greatly stimulated the field. In particular, Rainer Weiss at the Massachusetts Institute of Technology (MIT) started to think hard about detecting gravitational waves. In 1972, Weiss wrote a 23-page note in one of MIT’s quarterly newsletters, detailing for the first time the main experimental design and all sources of noise for a laser interferometer capable of detecting gravitational waves. This design would later become the foundation of the Laser Interferometer Gravitational-wave Observatory (LIGO) machines25.
The quietest place on Earth
The design of the detector used in LIGO (in Livingston, Louisiana and Hanford, Washington)—which is also used in the existing Virgo (near Pisa, Italy), GEO 600 (in Hanover, Germany) and KAGRA (in the Kamioka mines, Gifu Prefecture, Japan) detectors and will be used in the planned LIGO-India detector (in Hingoli, Maharashtra, India)—has an ‘L’ shape with equal-length arms connected to a corner station (see Fig. 1). When a typical gravitational wave passes by, at some phases of the wave one leg of the ‘L’ will be shortened and the other lengthened, and at other phases the reverse will happen. Thus, laser photons that bounce between the corner station and one end station return to the corner station later than laser photons that reflect off the other end station. As a result, the interference fringes produced when the light is combined at the corner station shift back and forth as the wave changes in phase. This shift can be compared with the expectations from different types of signals (for example, from binaries) to assess the probability that signal or noise is being observed.
a, Laser light is sent into the instrument to measure changes in the length of the two arms. b, A ‘beam splitter’ splits the light and sends out two identical beams along the arms. c, The light waves bounce off the mirror and return. d, A gravitational wave affects the interferometer’s arms differently: one extends and the other contracts as they pass from the peaks and troughs of the gravitational waves. e, Normally, the light returns unchanged to the beam splitter from both arms and the light waves cancel each other out. Image credit: ©Johan Jarnestad/The Royal Swedish Academy of Sciences.
This experimental setup raises an important question related to the smallness of the effect. To get a sense for the length changes that are measured, we note that the first directly detected gravitational waves had a maximum (dimensionless) fractional amplitude of 10−21, which means that the 4-km LIGO arms changed in length by 10−21 × 4 × 105 cm = 4 × 10−16 cm. Put differently, the effective force exerted by the gravitational waves is roughly 4 pN at 100 Hz, which is comparable to the weight of a eukaryotic cell at the frequency of a sonic toothbrush. Given that the proton radius is 10−13 cm, we are trying to measure distance changes of the order of 1/200 of the proton radius, with light that has a wavelength of the order of 10−4 cm. This seems impossible, even before we consider the many noise sources (for example, any shaking of the ground). The workaround is to have an enormous number of coherent photons that bounce around within the arms (in a Fabry–Perot configuration) many times before recombining. For N1 photons of wavelength λ, the location of the intensity peak can be measured with a precision of about \(\lambda /\sqrt{{N}_{1}}\). Similarly, for N2 bounces within the arms, the effective length of the interferometer, and thus the change in LIGO arm length, increases by a factor of N2. This means that for large enough N1 and N2, the necessary precision can be attained. A similar method is in fact used in astrometry observatories such as Gaia26, where the absolute angular localization of bright stars, about 10−5 arcsec, is far better than the about 0.1-arcsec angular resolution of its telescope.
Other noise sources—although substantial—can be managed for frequencies that are not too low. As an example, one might think that seismic noise would be a serious problem, but the detectors can be strongly shielded from shaking by the use of pendulum suspensions; for a pendulum of resonance frequency f0, the amplitude of oscillations with frequency f > f0 is reduced by a factor of about (f/f0)2. Thus the multi-stage pendulum suspension used by LIGO and Virgo can greatly reduce seismic noise. What cannot be shielded is so-called ‘Newtonian’ or ‘gravity gradient’ noise: pressure waves inside Earth travel because of a local (albeit small) change in the density of the rock; a temporarily increased density means that the region in question has greater mass and therefore greater gravity than it did before the pressure wave. This gravity enhancement pulls on the detector mirrors and, because we cannot shield anything from gravity, the noise must be reduced by one of three methods: delicate subtraction using feed-forward cancellation27, building the detector underground (because seismic waves have much bigger amplitudes on Earth’s surface) or placing the detector in space.
And then, there was sound
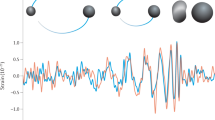
After more than four decades of thought and development, in the late summer of 2015 the LIGO detectors were finally sensitive enough to detect plausible astrophysical sources. On 14 September 2015, serendipity favoured physicists again: almost as soon as the detectors were turned on, they gave a signal that was strong enough to be an unmistakable source12 (see Fig. 2)—although given the importance of the discovery, the LIGO team spent months validating their analyses. Thus began the flood of results from the direct detection of gravitational waves, which have already had major impacts in fundamental physics, astrophysics and nuclear physics.
a, b, Two black holes several orbits before their merger (a), and at the point of merger (b). c, The aftermath of the merger; the remnant has settled down into its final state as a single black hole. On the vertical axis, strain is the fractional change in the arm lengths of the LIGO detectors. Figure adapted from ref. 91 (Springer Nature).
The LIGO detectors were actually designed as a physics experiment, and the avalanche of fundamental physics discoveries did not disappoint. Perhaps the most remarkable one is the 2017 measurement of the speed of gravitational waves28. According to Einstein, this speed should be equal to that of light, and indeed this is what the LIGO/Virgo and Fermi collaborations inferred, to an accuracy better than one part in 1015. As we describe later, this measurement was possible thanks to the gravitational-wave observation by LIGO and Virgo at the time of a neutron star binary merger, in coincidence with the short γ-ray burst that followed less than two seconds later and was detected using the Fermi observatory29. This single observation sufficed to place stringent constraints on violations of Lorentz invariance30,31, on violations of the equivalence principle32 and, in particular, on theoretical models that attempt to explain the late-time acceleration of the Universe through modified gravity instead of a dark-energy fluid33,34.
But that is not the only gold nugget hidden in the gravitational-wave mine. The very first gravitational-wave detection by the LIGO instruments in 2015 was generated by the merger of two black holes12. The signal-to-noise ratio of this event was so high (at roughly 25), and the event was so far away from Earth (at roughly 400 Mpc), that this single observation led to some of the most stringent model-independent constraints (at less than 10−22 eV) on the mass of the particle that is supposed to be responsible for mediating the gravitational interaction: the graviton35. Moreover, this single event confirmed that gravitational waves travel at the same speed irrespective of their frequency, just as predicted in the general theory of relativity36. This observation begins to dig into the parameter space of massive-graviton theories, which attempt to go beyond the early work of Fierz and Pauli37 through the inclusion of nonlinear interactions that evade certain otherwise unavoidable instabilities38,39.
The astrophysical implications of the direct detection of gravitational waves were equally important. Prior to the detections, the only category of LIGO-detectable astrophysical sources known to exist was binary neutron stars. As a result, the detector sensitivity and much of the science case for LIGO were built around predictions for the rate of detectable double neutron star coalescences. Some theoretical models of binary evolution predicted a high rate from double black holes with several tens of solar masses (for example, ref. 40), but the lack of any clear evidence for the existence of such black holes (the highest mass identified for any stellar-mass black hole in our Galaxy is only about 15Mʘ; Mʘ, solar mass) meant that the LIGO case could not be staked on such hypotheticals. The very first event seen with LIGO (which was called GW150914 because the waves reached Earth on 14 September 2015) was a coalescence between two black holes with masses of about 29Mʘ and 36Mʘ, leading to a final mass of about 62Mʘ (meaning that roughly 3Mʘ of mass energy was radiated in gravitational waves). Thus, the LIGO detections immediately doubled the mass range of known stellar-mass black holes, and then the merger doubled the range again (see Fig. 3)! The additional nine double black hole coalescences that have since been discovered have led to progressively tighter constraints on their formation rates, as well as to additional puzzles. For example, the inferred angular momenta for stellar-mass black holes seen in our Galaxy are typically sizeable fractions of the maximum allowed41, and alignment of those spins with the orbit in a binary black hole system is expected in the most popular scenario. Yet there are growing indications that the black holes observed in mergers usually have either low or misaligned spins (for example, ref. 42).
For the gravitational-wave detections, the masses of the original objects (black holes or neutron stars) and their final products are shown. Image credit: Frank Elavsky, LIGO-Virgo, Northwestern; adapted with permission from ref. 92.
An even greater astrophysical return was realized from the gravitational-wave detection and associated electromagnetic observations of what is so far the only double neutron star event29 seen: GW170817 (see Fig. 4). For this, the European Virgo detector made a key contribution to source localization, and the electromagnetic observations from radiofrequencies to γ-rays qualify as perhaps the most intense electromagnetic campaign ever focused on a single astronomical event. The associated short γ-ray burst validated a long-standing belief that double neutron star events can produce such bursts, and the subsequent optical and then infrared glow from this source corroborated predictions from the previous few years for the radioactive-decay-powered material expanding from such a merger43. The nature of the emission, particularly in the infrared, also supports the growing consensus that most of the elements considerably heavier than iron are produced by neutron star mergers, rather than by supernovae, as had been previously thought.
The gravitational waves from neutron star mergers may also open a new window of knowledge into the properties of the dense matter in neutron star cores. These properties are highly uncertain because (1) the microphysical conditions inside neutron stars (density of a few times the nuclear density, thermal energy much lower than the Fermi energy, and far more neutrons than protons) cannot be attained in terrestrial laboratories and (2) although neutron star mass measurements provide solid astrophysical constraints (for example, ref. 44), radius measurements are currently bedevilled by systematic errors (for example, refs 45,46).
To understand the potential contribution of gravitational-wave data, we note that as two neutron stars spiral towards each other, they act as point masses for most purposes when their separation is many times larger than their radii. However, at sufficiently close separations, tidal effects can cause the orbit to deviate from that of two point masses; in particular, orbital energy starts to be used to tidally deform the stars, which means that two neutron stars will spiral together roughly a millisecond faster than would two point masses of the same mass. The initial constraints on the properties of dense nuclear matter from GW170817 show the potential of gravitational waves for probing the interior of neutron stars (for example, refs 47,48). In particular, this one observation enabled the first attempt at a measurement of the tidal deformabilities of neutron stars, which has provided preliminary information about their equation of state. Future observations will improve these measurements, both because sensitivities at high frequency will be improved and because with more observations will come rare, very strong events that can be measured with exquisite precision.
When additional, somewhat uncertain, astrophysical assumptions are added, one can extract even more information about dense nuclear matter. For example, before the LIGO/Virgo detection of the double neutron star merger, a few groups argued that if the final product of the merger collapsed to a black hole shortly after merger, then it would be possible to use the measurement of the total mass of the neutron star binary to place an upper limit on the maximum mass of a non-rotating star. This upper limit could, in some cases, be much tighter than the about 2.8Mʘ upper limit allowed by current nuclear experiments49,50,51. Interpreted in this framework, the GW170817 data improve this limit greatly52, to about 2.2Mʘ, but this inference depends on astrophysical assumptions and thus the resulting constraints on neutron star matter are not as reliable as those following from, for example, the highest neutron star mass yet observed53 (of 2.01Mʘ ± 0.04Mʘ).
Gravitational-wave measurements of mergers involving neutron stars may even have an important future role in cosmology. Three decades ago, Bernard Schutz noted that because gravitational waves from a binary give information on the luminosity distance, and because if an electromagnetic counterpart can be established we also know the redshift, then coincident measurements give us a new way to measure the Hubble constant54 H0. It now seems possible that over the next several years, as tens to hundreds of neutron star coalescences are measured, this method may contribute considerably to our understanding of the expansion of the Universe55, although the accuracy of the Hubble constant may be ultimately limited by weak lensing (but see ref. 56) and degeneracies in the fitting of the cosmological model57.
The future is uncertain
The LIGO and Virgo era is far from finished. Plans for upgrades to the LIGO instruments are already being made. Among other advances, A+ (the planned advanced LIGO upgrade) will improve LIGO’s broadband sensitivity by using the technique of quantum light squeezing to reduce laser phase noise at high frequencies and radiation pressure noise at low frequencies. Squeezing, in its frequency-independent implementation, was demonstrated at the GEO 600 detector58; such a system has already been installed at both LIGO sites and in Virgo and is now operational in the current observing run O3. Projecting a bit further into the future, the proposed Voyager improvement to LIGO would replace the glass and suspensions with silicon parts and will operate at temperatures of around 120 K to lower thermal noise.
The United States with LIGO and Europe with Virgo are not the only players in gravitational-wave astronomy. Japan has built a 3-km underground interferometer, KAGRA, inside the Kamioka mines. This instrument will have the first implementation of cryogenic detection, and it is planned to join the LIGO and Virgo network in 2019. LIGO-India is hoped to be operational by the mid-2020s. When this occurs, the gravitational-wave network will be enhanced, with detectors spread all over the globe and able to detect gravitational waves from all directions at close-to-optimal sensitivities.
Predictions beyond 2025 are challenging, but plans for advanced ground-based instruments are already being made. Two possibilities are being discussed: the Einstein Telescope59, which is a project of several years’ standing, and the concept of the Cosmic Explorer60. Both will require new facilities, with the former planned as a triangular facility built underground to reduce seismic noise and the latter a 40-km-long detector using the quantum squeezing technology of A+ and the cryogenic cooling of KAGRA and Voyager. Funding has not yet been secured for these future facilities, although phase-A-type studies have begun, so one should not expect to see them deployed until the 2030s at the earliest.
The greater sensitivity of these improved detectors will lead to the precision era of gravitational-wave detection. Lower noise means essentially two things: many more events (in the thousands, depending on the unknown astrophysical event rate) at moderate signal-to-noise ratios from sources at distances of up to thousands of megaparsecs, and a few discoveries at very high signal-to-noise ratios (in the hundreds or more) from sources at distances of tens to hundreds of megaparsecs. The former will enable statistical studies of the mass and spin population of merging black holes, which will feed directly into astrophysical population synthesis models to understand how these massive beasts form in the first place (for example, ref. 61). The latter will yield better characterizations of the sources that emit such strong gravitational waves, perhaps permitting measurements of spin precession and orbital eccentricity. In turn, this information can be used to carry out more stringent tests of the general theory of relativity—for example, by introducing constraints on gravitational parity violation, which is otherwise degenerate with the binary’s spin62,63.
Other science targets of the next generation of ground-based detectors include intermediate-mass-ratio inspirals, the discovery of seed black holes, the stochastic gravitational-wave background, tests of the general theory of relativity with black hole quasinormal modes (which can also be obtained by stacking LIGO observations; see ref. 64) and the equation of state of the dense matter inside neutron stars. More speculative possibilities include detections of cosmic strings and of mergers of primordial black holes. Fundamentally, it is hoped that the improved sensitivity of the next detectors will provide surprises and yield unprecedented measurement precision.
A cosmic gravitational-wave detector
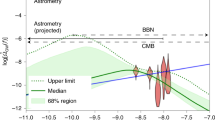
In addition to the roughly 10–2,000 Hz frequency range probed by current and planned ground-based gravitational-wave detectors, it is possible to use cosmic phenomena to infer the presence of lower-frequency gravitational waves. These include indirect measurements of waves of about 10−17–10−15 Hz from the presence of a certain type of polarization in the background microwave radiation of the Universe65 and the use of high-precision timing of pulsars to perform a different type of direct detection of gravitational waves of about 10−8–10−6 Hz (the nanohertz range).
This ambitious use of pulsars was conceived shortly after the detection of the first ‘millisecond pulsar’66 in 1982, on the basis of previous ideas by Sazhin67 and Detweiler68. Such pulsars spin rapidly, as is evident by their name, but more importantly their spin rates are nearly constant: some such pulsars will not increase their rotation periods by more than about 1 ms over ten billion years. Gravitational waves that pass between the pulsar and Earth could therefore be detected by the variation in the perceived frequency of the pulsars induced by the contraction and expansion of spacetime (see Fig. 5).
The signals from the pulsars travel through spacetime that is dynamically warped by gravitational waves, which changes the timing of the pulsars in a correlated way. Figure adapted from ref. 93 (Springer Nature).
However, there are practical issues to address. Although millisecond pulsars are very stable over a long time, their intrinsic pulse frequency is subject to poorly understood ‘red noise’, which has greater amplitude at lower frequencies. In addition, propagation effects through the interstellar medium, such as scintillation, can contribute additional noise.
In the same way that knowledge of the expected gravitational waveform improves the sensitivity of ground-based instruments to binary coalescences, we can use the anticipated characteristics of nanohertz sources to construct a template for the expected signal. In the nanohertz range, the strongest sources are probably binaries of supermassive black holes with masses of about 107Mʘ–1010Mʘ (other candidates include a primordial gravitational-wave background or gravitational waves from cosmic strings, but these are not expected to have high amplitudes). At the relevant frequencies, the inspiral time is thousands to millions of years; if we take as a rough estimate that there is a supermassive black hole binary merger once per year in the Universe, then there will be at least thousands of potential sources in the sky at the detectable frequencies. As a result, and in contrast to the sources so far detected using LIGO and Virgo, we expect a large set of sources at a given time that cannot be individually distinguished. Thus we expect a stochastic background of gravitational waves.
These are among the considerations that led R. W. Hellings and G. S. Downs69 to propose a template for pulsar-detected low-frequency gravitational waves. They pointed out that if the nanohertz gravitational-wave sky consists of many sources at once, then, to the lowest order, one would expect isotropy of the background. As a result, the main signature of timing deviations from gravitational waves, rather than other noise sources, is that the timing residual of pulsars at different locations should display a quadrupolar pattern. That is, the correlation between timing residuals in different directions should depend only on the angle between the directions.
This galactic-scale experiment is being carried out by three collaborations that use the world’s largest radio telescopes: the European Pulsar Timing Array (EPTA)70, the North American Nanohertz Observatory for Gravitational Waves (NANOGrav)71 and the Parkes Pulsar Timing Array (PPTA)72 in Australia, which all collaborate to form the International Pulsar Timing Array (IPTA). Again in contrast to the detections announced for high-frequency ground-based gravitational-wave detectors, detection of a stochastic background will occur via the slow accumulation of signal over many years. This signal, and possible even signals from individual supermassive binaries, are anticipated to be detected within the next decade73,74. Such detections will inform us about the mergers of galaxies and the dynamics of these black holes. In addition, because below about 10−8 Hz there are other processes that can cause supermassive black holes to spiral towards each other (such as interactions with gas or stars; see, for example, ref. 75), the detailed shape of the gravitational-wave spectrum below about 10−8 Hz may provide details of galactic centres that are otherwise inaccessible76.
Space, the final frontier
Ultimately, if we wish to detect gravitational waves emitted by a different type of strong-gravity source, we will have to go to space. A gravitational-wave detector in space would completely eliminate several noise sources, such as seismic, gravity-gradient and anthropogenic noise, although at the same time it would introduce other substantial complications. A mission that is expected to accomplish this is the Laser Interferometer Space Antenna (LISA)77 (see Fig. 6). LISA is an European Space Agency mission, with a junior partnership contribution by NASA (and based on ideas related to drag-free satellites dating back to the 1970s; for example, ref. 78), which will consist of an arrangement of three satellites in orbit around the Sun and trailing Earth, maintaining a triangular arrangement that precesses as it moves around the Sun. Inside each satellite, a shielded and isolated test cube will fall freely through space, tracing a path that will only be perturbed by gravitational waves. Because the satellites will be millions of kilometres away from each other, LISA will measure the relative position of the test cubes through time-delay interferometry, with the signal being sent around the triangle one or more times before being brought into interference, with the processing of the phase differences performed a posteriori using software79. A similar mission, TianQin, has recently also been proposed, with a sensitivity band roughly an order of magnitude higher in frequency80.
Unlike ground-based detectors, such as LIGO and Virgo, in LISA the stations are free-floating test masses in orbit around the Sun. Figure adapted from ref. 93 (Springer Nature).
LISA is a technically ambitious mission. Indeed, it created enough scepticism that funding for the mission was at one point contingent on the success of a technological demonstration, LISA Pathfinder. In essence, Pathfinder had to show that it could launch a single LISA-type satellite with a shielded and isolated test cube inside, and that the test cube would fall freely as the satellite orbits around the Sun, with any residual relative acceleration below 10−15 m s−2. Pathfinder was a remarkable success, as it exceeded this requirement by more than one order of magnitude81. LISA is scheduled to launch by 2034.
Once LISA is operational, it will detect entire new classes of gravitational waves. One of the most anticipated classes is the waves generated in the merger of black holes with masses of about 104Mʘ–107Mʘ at the centres of galaxies. Such events occur in the millihertz band, which cannot be detected using ground-based instruments (but might be detectable as bursts with lasting ‘memory’ effects seen in pulsar timing82). These gravitational waves encode a trove of information about the properties of black holes hosted at the centre of galaxies before the galaxies collide, feeding again into astrophysical population modelling. Another anticipated source of gravitational waves is the inspiral of a small black hole or neutron star into a supermassive black hole. In these extreme-mass-ratio inspirals83, the small compact object zooms and whirls around the supermassive black hole, emitting millihertz-frequency gravitational waves for years in the band covered by LISA. Ground-based detectors are again deaf to these waves, which carry information about the curvature of spacetime in the vicinity of supermassive black holes. There is the possibility of linking these types of detectors if a stellar-mass black hole binary is first detected by LISA and then—months to years later—detected by third-generation or upgraded detectors on the ground84,85.
Space-based gravitational-wave observations are crucial because of the unique science that they enable. On the astrophysical front, the properties of supermassive black holes when galaxies merge can only be determined through these waves. Moreover, owing to the sensitivity of these detectors, one could in principle see events with redshifts of up to 20—essentially to the beginning of when we expect such black holes to exist—and trace the evolution of the cosmic web. On the theoretical physics front, the spacetime of supermassive black holes, as traced by a small compact object, is encoded in vast detail by gravitational waves emitted in extreme-mass-ratio inspirals86,87. Such observations will allow us to test the hypothesis that black holes in the Universe are described by the solution to the Einstein equations found in the 1960s by Roy Kerr88. Moreover, the chirping of these waves will allow us to simultaneously test the dynamics of these inspirals, perform new tests of the equivalence principle and constrain gravitational parity violation and Lorentz violation much better than before in the extreme-gravity regime62,89. The detection of mergers of supermassive black holes at high signal-to-noise ratios will also allow us to probe how efficiently the merged remnant settles down to a Kerr black hole through the emission of quasinormal modes, as predicted by Einstein’s theory90.
If the past is a good predictor for the future, these tests will once more verify that Einstein was right all along, that many models of modified gravity must be discarded and that some particular model (or models) of black hole formation are applicable in nature. However, there can be—and probably will be—surprises. Every time humankind has opened a new window into the Universe, unexpected discoveries have emerged. These discoveries are coveted because they will provide a hint of how to answer some fundamental questions in gravitational physics that remain unanswered. What is causing the late time acceleration of the Universe? What is causing the rotation curves of galaxies? How do we unify quantum mechanics with gravity? Gravitational waves have the potential to provide expected and unexpected clues to these questions that we can use to put together the jigsaw puzzle of our mysterious Universe.
References
Einstein, A. Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Ann. Phys. 322, 132–148 (1905).
Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 322, 549–560 (1905).
Einstein, A. Zur Elektrodynamik bewegter Körper. Ann. Phys. 322, 891–921 (1905).
Einstein, A. Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig? Ann. Phys. 323, 639–641 (1905).
Einstein, A. Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen. Jahrb. Radioaktivität Elektronik 4, 411–462 (1908).
Einstein, A. Erklarung der Perihelionbewegung der Merkur aus der allgemeinen Relativitatstheorie. Sitzungsber. Preuss. Akad. Wiss. 47, 831–839 (1915).
Dyson, F. W., Eddington, A. S. & Davidson, C. A determination of the deflection of light by the Sun’s gravitational field, from observations made at the total eclipse of May 29, 1919. Phil. Trans. R. Soc. Lond. A 220, 291–333 (1920). This paper reported that observations of the 1919 solar eclipse confirmed Einstein’s prediction of gravitational light deflection.
Campbell, W. W. & Trumpler, R. Observations on the deflection of light in passing through the sun’s gravitational field, made during the total solar eclipse of September 21, 1923. Astron. Soc. Pac. 35, 158–163 (1923).
Popper, D. M. Red shift in the spectrum of 40 Eridani B. Astrophys. J. 120, 316–321 (1954).
Pound, R. V. & Rebka, G. A. Apparent weight of photons. Phys. Rev. Lett. 4, 337–341 (1960).
Shapiro, I. I. Fourth test of general relativity. Phys. Rev. Lett. 13, 789–791 (1964).
LIGO Scientific Collaboration & Virgo Collaboration. Observation of gravitational waves from a binary black hole merger. Phys. Rev. Lett. 116, 061102 (2016). First announcement of the direct detection of gravitational waves (from a double black hole binary).
Einstein, A. Näherungsweise Integration der Feldgleichungen der Gravitation. Sitzungsber. K. Preuß. Akad. der Wiss. 1916, 688–696 (1916). First paper to propose the existence of gravitational waves.
Einstein, A. Über Gravitationswellen. Sitzungsber. K. Preuß. Akad. der Wiss. 1918, 154–167 (Verlag der Akademie der Wissenschaften, 1918).
Eddington, A. S. The propagation of gravitational waves. Proc. R. Soc. Lond. A 102, 268–282 (1922).
Rickles, D. & DeWitt, C. M. (eds). The Role of Gravitation in Physics (Edition Open Access, Berlin, 2011).
Weber, J. & Wheeler, J. A. Reality of the cylindrical gravitational waves of Einstein and Rosen. Rev. Mod. Phys. 29, 509–515 (1957).
Hewish, A., Bell, S. J., Pilkington, J. D. H., Scott, P. F. & Collins, R. A. Observation of a rapidly pulsating radio source. Nature 217, 709–713 (1968).
Gold, T. Rotating neutron stars as the origin of the pulsating radio sources. Nature 218, 731–732 (1968).
Peters, P. C. & Mathews, J. Gravitational radiation from point masses in a Keplerian orbit. Phys. Rev. 131, 435–440 (1963).
Peters, P. C. Gravitational radiation and the motion of two point masses. Phys. Rev. 136, B1224–B1232 (1964).
Hulse, R. A. & Taylor, J. H. Discovery of a pulsar in a binary system. Astrophys. J. 195, L51–L53 (1975). First study to show the existence of binary neutron stars.
Weisberg, J. M. & Taylor, J. H. Gravitational radiation from an orbiting pulsar. Gen. Relativ. Gravit. 13, 1–6 (1981).
Weber, J. Evidence for discovery of gravitational radiation. Phys. Rev. Lett. 22, 1320–1324 (1969).
Weiss, R. Electromagnetically Coupled Broadband Gravitational Wave Antenna. Quarterly Progress Report 105 84–107 (MIT, 1972). Seminal paper that laid out the noise sources and their magnitudes for detectors such as the modern-day LIGO and Virgo detectors.
Gaia Collaboration. The Gaia mission. Astron. Astrophys. 595, A1 (2016).
Coughlin, M. et al. Towards a first design of a Newtonian noise cancellation system for Advanced LIGO. Class. Quantum Gravity 33, 244001 (2016).
Abbott, B. P. et al. Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB170817A. Astrophys. J. 848, L13 (2017). First detection of gravitational waves from a double neutron star binary.
LIGO Scientific Collaboration & Virgo Collaboration. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101 (2017).
Oost, J., Mukohyama, S. & Wang, A. Constraints on Einstein-aether theory after GW170817. Phys. Rev. D 97, 124023 (2018).
Gong, Y., Hou, S., Liang, D. & Papantonopoulos, E. Gravitational waves in Einstein-aether and generalized TeVeS theory after GW170817. Phys. Rev. D 97, 084040 (2018).
Wei, J.-J. et al. Multimessenger tests of the weak equivalence principle from GW170817 and its electromagnetic counterparts. J. Cosmol. Astropart. Phys. 1711, 035 (2017).
Ezquiaga, J. M. & Zumalacárregui, M. Dark energy after GW170817: dead ends and the road ahead. Phys. Rev. Lett. 119, 251304 (2017).
Baker, T. et al. Strong constraints on cosmological gravity from GW170817 and GRB 170817A. Phys. Rev. Lett. 119, 251301 (2017).
LIGO Scientific Collaboration & Virgo Collaboration. Tests of general relativity with GW150914. Phys. Rev. Lett. 116, 221101 (2016); erratum 121, 129902 (2018).
Yunes, N., Yagi, K. & Pretorius, F. Theoretical physics implications of the binary black-hole mergers GW150914 and GW151226. Phys. Rev. D 94, 084002 (2016).
Fierz, M. & Pauli, W. On relativistic wave equations for particles of arbitrary spin in an electromagnetic field. Proc. R. Soc. Lond. A 173, 211–232 (1939).
de Rham, C., Gabadadze, G. & Tolley, A. J. Resummation of massive gravity. Phys. Rev. Lett. 106, 231101 (2011).
Hassan, S. F. & Rosen, R. A. Resolving the ghost problem in non-linear massive gravity. Phys. Rev. Lett. 108, 041101 (2012).
Belczynski, K. et al. The effect of metallicity on the detection prospects for gravitational waves. Astrophys. J. 715, L138–L141 (2010).
Miller, M. C. & Miller, J. M. The masses and spins of neutron stars and stellar-mass black holes. Phys. Rep. 548, 1–34 (2015).
Farr, W. M. et al. Distinguishing spin-aligned and isotropic black hole populations with gravitational waves. Nature 548, 426–429 (2017).
Li, L.-X. & Paczyński, B. Transient events from neutron star mergers. Astrophys. J. 507, L59–L62 (1998).
Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E. & Hessels, J. W. T. A two-solar-mass neutron star measured using Shapiro delay. Nature 467, 1081–1083 (2010).
Miller, M. C. Astrophysical constraints on dense matter in neutron stars. Preprint at https://arxiv.org/abs/1312.0029 (2013).
Miller, M. C. & Lamb, F. K. Observational constraints on neutron star masses and radii. Eur. Phys. J. A 52, 63 (2016).
De, S. et al. Tidal deformabilities and radii of neutron stars from the observation of GW 170817. Phys. Rev. Lett. 121, 091102 (2018).
LIGO Scientific Collaboration. GW170817: measurements of neutron star radii and equation of state. Preprint at https://arxiv.org/abs/1805.11581 (2018).
Bauswein, A., Baumgarte, T. W. & Janka, H.-T. Prompt merger collapse and the maximum mass of neutron stars. Phys. Rev. Lett. 111, 131101 (2013).
Fryer, C. L. et al. The fate of the compact remnant in neutron star mergers. Astrophys. J. 812, 24 (2015).
Lawrence, S., Tervala, J. G., Bedaque, P. F. & Miller, M. C. An upper bound on neutron star masses from models of short gamma-ray bursts. Astrophys. J. 808, 186 (2015).
Margalit, B. & Metzger, B. D. Constraining the maximum mass of neutron stars from multi-messenger observations of GW170817. Astrophys. J. 850, L19 (2017).
Antoniadis, J. et al. A massive pulsar in a compact relativistic binary. Science 340, 1233232 (2013).
Schutz, B. F. Determining the Hubble constant from gravitational wave observations. Nature 323, 310–311 (1986).
Chen, H.-Y., Fishbach, M. & Holz, D. E. A two per cent Hubble constant measurement from standard sirens within five years. Nature 562, 545–547 (2018).
Hirata, C. M., Holz, D. E. & Cutler, C. Reducing the weak lensing noise for the gravitational wave Hubble diagram using the non-Gaussianity of the magnification distribution. Phys. Rev. D 81, 124046 (2010).
Shafieloo, A., Keeley, R. E. & Linder, E. V. Will gravitational wave sirens determine the Hubble constant? Preprint at https://arxiv.org/abs/1812.07775 (2018).
LIGO Scientific Collaboration. A gravitational wave observatory operating beyond the quantum shot-noise limit. Nat. Phys. 7, 962–965 (2011).
Punturo, M. et al. The Einstein Telescope: a third-generation gravitational wave observatory. Class. Quantum Gravity 27, 194002 (2010).
Abbott, B. P. et al. Exploring the sensitivity of next generation gravitational wave detectors. Class. Quantum Gravity 34, 044001 (2017).
Barrett, J. W. et al. Accuracy of inference on the physics of binary evolution from gravitational-wave observations. Mon. Not. R. Astron. Soc. 477, 4685–4695 (2018).
Yunes, N. & Siemens, X. Gravitational-wave tests of general relativity with ground-based detectors and pulsar timing-arrays. Living Rev. Relativ. 16, 9 (2013).
Alexander, S. H. & Yunes, N. Gravitational wave probes of parity violation in compact binary coalescences. Phys. Rev. D 97, 064033 (2018).
Yang, H. et al. Black hole spectroscopy with coherent mode stacking. Phys. Rev. Lett. 118, 161101 (2017).
Polnarev, A. G. Polarization and anisotropy induced in the microwave background by cosmological gravitational waves. Sov. Astron. 62, 1041–1052 (1985).
Backer, D. C., Kulkarni, S. R., Heiles, C., Davis, M. M. & Goss, W. M. A millisecond pulsar. Nature 300, 615–618 (1982).
Sazhin, M. V. Opportunities for detecting ultralong gravitational waves. Sov. Astron. 22, 36–38 (1978).
Detweiler, S. L. Pulsar timing measurements and the search for gravitational waves. Astrophys. J. 234, 1100–1104 (1979).
Hellings, R. W. & Downs, G. S. Upper limits on the isotropic gravitational radiation background from pulsar timing analysis. Astrophys. J. 265, L39–L42 (1983).
Stappers, B. W., Kramer, M., Lyne, A. G., D’Amico, N. & Jessner, A. The European Pulsar Timing Array. Chin. J. Astron. Astrophys. Suppl. Ser. 6, 298–303 (2006).
Jenet, F. et al. The North American Nanohertz Observatory for Gravitational waves. Preprint at https://arxiv.org/abs/0909.1058 (2009).
Manchester, R. The Parkes Pulsar Timing Array and detection of gravitational waves. In 36th COSPAR Scientific Assembly Vol. 36 (COSPAR, 2006).
Taylor, S. R. et al. Are we there yet? Time to detection of nanohertz gravitational waves based on pulsar-timing array limits. Astrophys. J. 819, L6 (2016).
Mingarelli, C. M. F. et al. The local nanohertz gravitational wave landscape from supermassive black hole binaries. New Astron. 1, 886–892 (2017).
Sesana, A. Insights into the astrophysics of supermassive black hole binaries from pulsar timing observations. Class. Quantum Gravity 30, 224014 (2013).
Arzoumanian, Z. et al. The NANOGrav 11 year data set: pulsar-timing constraints on the stochastic gravitational-wave background. Astrophys. J. 859, 47 (2018).
Amaro-Seoane, P. et al. Laser Interferometer Space Antenna. Preprint at https://arxiv.org/abs/1702.00786 (2017).
Weiss, R. in Sources of Gravitational Radiation (ed. Smarr, L. L.) 7–35 (Cambridge Univ. Press, Cambridge, 1979).
Tinto, M. & Dhurandhar, S. V. Time-delay interferometry. Living Rev. Relativ. 17, 6 (2014).
Luo, J. et al. TianQin: a space-borne gravitational wave detector. Class. Quantum Gravity 33, 035010 (2016).
Armano, M. et al. Beyond the required LISA free-fall performance: new LISA Pathfinder results down to 20 μHz. Phys. Rev. Lett. 120, 061101 (2018).
van Haasteren, R. & Levin, Y. Gravitational-wave memory and pulsar timing arrays. Mon. Not. R. Astron. Soc. 401, 2372–2378 (2010).
Amaro-Seoane, P. Relativistic dynamics and extreme mass ratio inspirals. Living Rev. Relativ. 21, 4 (2018).
Miller, M. C. Gravitational radiation from intermediate-mass black holes. Astrophys. J. 581, 438–450 (2002).
Sesana, A. Prospects for multiband gravitational-wave astronomy after GW150914. Phys. Rev. Lett. 116, 231102 (2016).
Ryan, F. D. Gravitational waves from the inspiral of a compact object into a massive, axisymmetric body with arbitrary multipole moments. Phys. Rev. D 52, 5707–5718 (1995).
Collins, N. A. & Hughes, S. A. Towards a formalism for mapping the space-times of massive compact objects: bumpy black holes and their orbits. Phys. Rev. D. 69, 124022 (2004).
Kerr, R. P. Gravitational field of a spinning mass as an example of algebraically special metrics. Phys. Rev. Lett. 11, 237–238 (1963). Derivation of the exterior spacetime that applies to all astrophysical black holes (including angular momentum and mass—but no electric charge).
Gair, J. R., Vallisneri, M., Larson, S. L. & Baker, J. G. Testing general relativity with low-frequency, space-based gravitational-wave detectors. Living Rev. Relativ. 16, 7 (2013).
Dreyer, O. et al. Black hole spectroscopy: testing general relativity through gravitational wave observations. Class. Quantum Gravity 21, 787–804 (2004).
Miller, M. C. Dawn of a new astronomy. Nature 531, 40–42 (2016).
Mandel, I. & Farmer, A. Merging stellar-mass binary black holes. Preprint at https://arxiv.org/abs/1806.05820 (2018).
Castelvecchi, D. Here come the waves. Nature 556, 164–168 (2018).
Acknowledgements
We thank R. Adhikari, C. Chirenti, S. Hughes, I. Mandel, M. McLaughlin and B. Schutz for suggestions that helped improve this manuscript. We thank S. Hughes for suggesting the animal cell example.
Author information
Authors and Affiliations
Contributions
M.C.M. led the discussion of astrophysical implications and N.Y. led the discussion of implications for strong gravity. Both authors edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Miller, M.C., Yunes, N. The new frontier of gravitational waves. Nature 568, 469–476 (2019). https://doi.org/10.1038/s41586-019-1129-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1129-z
This article is cited by
-
High-energy neutrino transients and the future of multi-messenger astronomy
Nature Reviews Physics (2022)
-
Fast radio bursts at the dawn of the 2020s
The Astronomy and Astrophysics Review (2022)
-
Gravitomagnetic induction in the field of a gravitational wave
General Relativity and Gravitation (2022)
-
To the Thomson Cross Section of Light Scattered by a Moving Particle
Journal of Russian Laser Research (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.