Abstract
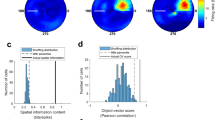
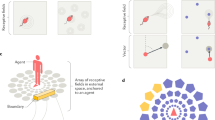
The hippocampus and the medial entorhinal cortex are part of a brain system that maps self-location during navigation in the proximal environment1,2. In this system, correlations between neural firing and an animal’s position or orientation are so evident that cell types have been given simple descriptive names, such as place cells3, grid cells4, border cells5,6 and head-direction cells7. While the number of identified functional cell types is growing at a steady rate, insights remain limited by an almost-exclusive reliance on recordings from rodents foraging in empty enclosures that are different from the richly populated, geometrically irregular environments of the natural world. In environments that contain discrete objects, animals are known to store information about distance and direction to those objects and to use this vector information to guide navigation8,9,10. Theoretical studies have proposed that such vector operations are supported by neurons that use distance and direction from discrete objects11,12 or boundaries13,14 to determine the animal’s location, but—although some cells with vector-coding properties may be present in the hippocampus15 and subiculum16,17—it remains to be determined whether and how vectorial operations are implemented in the wider neural representation of space. Here we show that a large fraction of medial entorhinal cortex neurons fire specifically when mice are at given distances and directions from spatially confined objects. These ‘object-vector cells’ are tuned equally to a spectrum of discrete objects, irrespective of their location in the test arena, as well as to a broad range of dimensions and shapes, from point-like objects to extended surfaces. Our findings point to vector coding as a predominant form of position coding in the medial entorhinal cortex.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Data sets supporting the findings of this paper are available on request from the corresponding authors.
Code availability
Custom code is available from the corresponding authors on request.
References
O’Keefe, J. & Nadel, L. The Hippocampus as a Cognitive Map (Oxford Univ. Press, Oxford, 1978).
Moser, E. I., Kropff, E. & Moser, M. B. Place cells, grid cells, and the brain’s spatial representation system. Annu. Rev. Neurosci. 31, 69–89 (2008).
O’Keefe, J. & Dostrovsky, J. The hippocampus as a spatial map. Preliminary evidence from unit activity in the freely-moving rat. Brain Res. 34, 171–175 (1971).
Hafting, T., Fyhn, M., Molden, S., Moser, M. B. & Moser, E. I. Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806 (2005).
Savelli, F., Yoganarasimha, D. & Knierim, J. J. Influence of boundary removal on the spatial representations of the medial entorhinal cortex. Hippocampus 18, 1270–1282 (2008).
Solstad, T., Boccara, C. N., Kropff, E., Moser, M. B. & Moser, E. I. Representation of geometric borders in the entorhinal cortex. Science 322, 1865–1868 (2008).
Taube, J. S., Muller, R. U. & Ranck, J. B. Jr. Head-direction cells recorded from the postsubiculum in freely moving rats. I. Description and quantitative analysis. J. Neurosci. 10, 420–435 (1990).
Collett, T. S., Cartwright, B. A. & Smith, B. A. Landmark learning and visuo-spatial memories in gerbils. J. Comp. Physiol. A 158, 835–851 (1986).
Biegler, R. & Morris, R. G. Landmark stability is a prerequisite for spatial but not discrimination learning. Nature 361, 631–633 (1993).
Hurly, T. A., Fox, T. A., Zwueste, D. M. & Healy, S. D. Wild hummingbirds rely on landmarks not geometry when learning an array of flowers. Anim. Cogn. 17, 1157–1165 (2014).
McNaughton, B. L., Knierim, J. J. & Wilson, M. A. in The Cognitive Neurosciences (ed. M.S. Gazzaniga) 585–595 (MIT Press, 1995).
Stemmler, M., Mathis, A. & Herz, A. V. Connecting multiple spatial scales to decode the population activity of grid cells. Sci. Adv. 1, e1500816 (2015).
O’Keefe, J. & Burgess, N. Geometric determinants of the place fields of hippocampal neurons. Nature 381, 425–428 (1996).
Burgess, N., Jackson, A., Hartley, T. & O’Keefe, J. Predictions derived from modelling the hippocampal role in navigation. Biol. Cybern. 83, 301–312 (2000).
Deshmukh, S. S. & Knierim, J. J. Influence of local objects on hippocampal representations: landmark vectors and memory. Hippocampus 23, 253–267 (2013).
Barry, C. et al. The boundary vector cell model of place cell firing and spatial memory. Rev. Neurosci. 17, 71–97 (2006).
Lever, C., Burton, S., Jeewajee, A., O’Keefe, J. & Burgess, N. Boundary vector cells in the subiculum of the hippocampal formation. J. Neurosci. 29, 9771–9777 (2009).
Deshmukh, S. S. & Knierim, J. J. Representation of non-spatial and spatial information in the lateral entorhinal cortex. Front. Behav. Neurosci. 5, 69 (2011).
Tsao, A., Moser, M. B. & Moser, E. I. Traces of experience in the lateral entorhinal cortex. Curr. Biol. 23, 399–405 (2013).
Deshmukh, S. S., Johnson, J. L. & Knierim, J. J. Perirhinal cortex represents nonspatial, but not spatial, information in rats foraging in the presence of objects: comparison with lateral entorhinal cortex. Hippocampus 22, 2045–2058 (2012).
Weible, A. P., Rowland, D. C., Monaghan, C. K., Wolfgang, N. T. & Kentros, C. G. Neural correlates of long-term object memory in the mouse anterior cingulate cortex. J. Neurosci. 32, 5598–5608 (2012).
Sargolini, F. et al. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312, 758–762 (2006).
Kropff, E., Carmichael, J. E., Moser, M. B. & Moser, E. I. Speed cells in the medial entorhinal cortex. Nature 523, 419–424 (2015).
Sarel, A., Finkelstein, A., Las, L. & Ulanovsky, N. Vectorial representation of spatial goals in the hippocampus of bats. Science 355, 176–180 (2017).
Wang, C. et al. Egocentric coding of external items in the lateral entorhinal cortex. Science 362, 945–949 (2018).
Muller, R. U. & Kubie, J. L. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J. Neurosci. 7, 1951–1968 (1987).
Fyhn, M., Hafting, T., Treves, A., Moser, M. B. & Moser, E. I. Hippocampal remapping and grid realignment in entorhinal cortex. Nature 446, 190–194 (2007).
Yoganarasimha, D., Yu, X. & Knierim, J. J. Head direction cell representations maintain internal coherence during conflicting proximal and distal cue rotations: comparison with hippocampal place cells. J. Neurosci. 26, 622–631 (2006).
Gardner, R. J., Lu, L., Wernle, T., Moser, M. B. & Moser, E. I. Correlation structure of grid cells is preserved during sleep. Nat. Neurosci. (in the press) (2019).
Trettel, S. G., Trimper, J. B., Hwaun, E., Fiete, I. R. & Colgin, L. L. Grid cell co-activity patterns during sleep reflect spatial overlap of grid fields during active behaviors. Nat. Neurosci. (in the press) (2019).
Schmitzer-Torbert, N., Jackson, J., Henze, D., Harris, K. & Redish, A. D. Quantitative measures of cluster quality for use in extracellular recordings. Neuroscience 131, 1–11 (2005).
Skaggs, W. E., McNaughton, B. L., Gothard, K. M. & Markus, E. J. in Advances in Neural Information Processing Systems 5 (eds. Hanson, S. J., Cowan, J. D. & Giles, C. L.) 1030–1037 (Morgan Kaufmann, 1993).
Langston, R. F. et al. Development of the spatial representation system in the rat. Science 328, 1576–1580 (2010).
Acknowledgements
We thank A. M. Amundsgård, K. Haugen, K. Jenssen, V. Frolov, I. U. Kruge, N. Dagslott, E. Kråkvik and H. Waade for technical assistance. The work was supported by two Advanced Investigator Grants from the European Research Council (GRIDCODE, Grant Agreement N°338865; ENSEMBLE – Grant Agreement N°268598), a NEVRONOR grant from the Research Council of Norway (grant no. 226003), the Centre of Excellence scheme and the National Infrastructure Scheme of the Research Council of Norway (Centre for Neural Computation, grant number 223262; NORBRAIN1, grant number 197467), the Louis Jeantet Prize, the Körber Prize and the Kavli Foundation.
Reviewer information
Nature thanks Martin Stemmler and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
Ø.A.H., M.-B.M. and E.I.M. designed most experiments and analytic approaches; Ø.A.H., E.R.S. and S.O.A. collected data; Ø.A.H. performed analyses; M.-B.M. and E.I.M. supervised the project; Ø.A.H. and E.I.M. wrote the paper with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Recording locations in the MEC.
Representative examples of Nissl-stained sagittal brain sections showing tetrode locations for 8 of the 16 mice used for experiments. Mouse identifer (ID) numbers are indicated above each section. Pairs of black arrowheads indicate the dorsoventral range of the recording locations. Scale bar, 250 µm.
Extended Data Fig. 2 List of all objects used to identify object-vector cells.
a, All objects used in experiments with object-vector cells. Objects had either a prism-like or cylinder-like appearance, with some modifications, and varied in height and width. b, Shape, dimensions, colour and material of each object, numbered as in a. c, Prismatic objects of increasing length used for experiment in which a point-like prism tower was changed across trials into a lengthy wall. Objects consisted of 21-cm-high, 3-cm-wide towers of Duplo Lego bricks with lengths of 6.75 cm, 25 cm, 37.5 cm and 62.5 cm. d, Cardboard cylinders of increasing diameter (2 cm, 5 cm, 10 cm, 15 cm and 20 cm). e, Prismatic Duplo Lego objects of increasing height (2 cm, 10 cm, 20 cm and 40 cm).
Extended Data Fig. 3 Ellipticity of object-vector fields.
To more formally characterize the firing of object-vector cells, we compared two models of vector-determined firing, with firing fields corresponding to a Gaussian circle or an ellipse. The models were applied to the raw, unsmoothed firing rate maps. a, A slightly better fit is usually obtained from the elliptic model. Left to right: (1) path plot of an object-vector cell; (2) unsmoothed firing rate map of the cell; (3) object-vector field obtained by fitting an elliptic model to the raw unsmoothed firing rate map of the cell; and (4) object-vector field obtained by fitting a Gaussian model to the raw unsmoothed firing rate map. For this cell, the elliptic fit explained 3.2% more of the underlying data (the unsmoothed firing rate map) than the Gaussian circle model. b, Left, frequency distributions showing relative goodness of fit (see Methods) of the elliptic and circular models. Right, aspect ratio (ratios between s.d. values in two dimensions) for all object-vector cells. Aspect ratios for the best fit had a median of 1.6 and 25th–75th percentiles of 1.3–2.0. An aspect ratio near 1 indicates that the firing field is almost circular.
Extended Data Fig. 4 Object-vector cells are distinct from other spatially modulated cell classes.
a, Colour-coded rate maps (top) and path plots (bottom) for two representative object-vector cells recorded first without an object and then with an object (white circle). Path plots show the mouse’s trajectory with spike locations superimposed as black dots. Peak rates, and mouse and cell ID numbers, are indicated (horizontal and vertical text labels, respectively). The cells responded vigorously to objects but did not have border or grid fields. In the no-object condition, 15 of 162 object-vector cells also passed the border cell criteria and 4 passed the criteria for grid cells. Lowering the minimum threshold for peak firing rate from 2 Hz to 1.5 Hz made no discernible difference: 163 cells passed the criteria for object-vector cells, and 18 of these cells passed the border cell criteria and 4 cells the grid cell criteria. b, Distribution of border scores, grid scores, speed scores, and head-direction scores for object-vector cells on trials without an object (dark blue boxes, n = 162), for object-vector cells on trials with an object (light blue boxes, n = 162), and for cells that did not satisfy criteria for object-vector cells on the no-object trial, including all other types of spatially or directionally modulated cells (light grey boxes, n = 938). Without objects present, border scores were higher in the overall population than in object-vector cells (Mann–Whitney U-test, U = 5.7 × 104, P = 0.0002). Grid scores were also higher in the overall population than in object-vector cells (Mann–Whitney U-test, U = 6.2 × 104, P = 1.1 × 10−10). By contrast, head-direction scores were higher for object-vector cells than for the remaining cells when objects were not present (Mann–Whitney U-test, U = 1.1 × 105, P = 1.6 × 10−7), which suggests that a subset of object-vector cells is modulated by head-direction input. Head-direction tuning of object-vector cells decreased significantly when objects were present (Wilcoxon signed rank test, W = 10,206, P = 1.7 × 10−9) and was then not different from that of the overall population (Mann–Whitney U-test, U = 93,560, P = 0.24). Speed scores were not different for object-vector cells compared to the remaining cells (Mann–Whitney U-test, U = 8.4 × 104, P = 0.18). All statistical tests were two-sided. Black line between box edges indicates median, box edges indicate 25th and 75th percentiles, whiskers extend to the most extreme point that lies within 1.5 × interquartile range (IQR), and data points larger than 1.5 × IQR are considered outliers (red crosses). c, Response to object in an object-vector cell with significant tuning to head direction of the mouse. Left, recording with no object; right, with an object. For each trial, a colour-coded firing rate map is shown with a circular plot for firing rate as a function of head direction (black curve, firing rate; blue curve, time spent; HD, head-direction score (that is, mean vector length)). Peak rates are indicated for rate maps and directional tuning plots. The dispersed directional tuning on the baseline trial is typical; most direction-tuned object-vector cells had wide or multipeaked tuning curves (unlike those of ‘classical’ head-direction cells8). Note that this weak head-direction tuning is reduced when the object is introduced. d, Head-direction score for all object-vector cells that passed the head-direction criteria on the no-object trial, plotted against the head-direction score of the same cells on the object trial. Note the general reduction in head-direction tuning when the object is present. e, Colour-coded rate maps for three object-vector cells with two object-vector fields. Object-vector fields are indicated by black open circles. Small filled white circles represent objects. Large white and open circles indicate template areas in a regular grid lattice extrapolated from the positions of the two object-vector fields. A grid-pattern Z-score was calculated by first determining the difference between the mean firing rate inside the extrapolated areas (large white and open circles) and the mean firing rate outside all projected and real firing fields, and then dividing this difference by the s.d. of the firing rate. Z-scores and peak firing rates are indicated below each example map. Mouse and cell ID numbers are indicated at the top. f, Grid-pattern Z-scores, calculated as in e, for the entire population of object-vector cells with multiple object-vector fields (n = 56 cells). Box plot as in b. Fluctuation of Z-scores around 0 (median −0.12, 25th–75th percentiles −0.24 to 0.07) suggests that the two (or three) fields of the object-vector cells are not part of a regular grid pattern.
Extended Data Fig. 5 Spike clusters of object-vector cells with two discrete firing fields.
Separation of spikes from object-vector cells with two firing fields from spikes of other simultaneously recorded MEC cells. a, Examples of cell separation in 2D projections of multidimensional cluster diagrams. First and third columns, colour-coded rate maps showing two distinct object-vector cells, with mouse and cell ID numbers (top) and peak rates (bottom) indicated. Second and fourth columns, scatter plots showing relationship between energy (square of signal) for spikes recorded from two selected electrodes of a tetrode in the recording that contains the object-vector cell in the rate map to the left. The electrode numbers in each pair are indicated on axis labels. Each dot represents one sampled signal. Clusters are likely to correspond to spikes that originate from the same cell. The cluster giving rise to the rate map to the left of each scatter plot is shown in black; remaining signals in grey. L-ratio and isolation distance31 for cluster in black are indicated above the scatter plot. Note clear separation of the object-vector cell from other spikes, which suggests that it is unlikely that second fields reflected contamination of spikes from other cells. b, Distribution of L-ratio and isolation distance for all object-vector cells with one field (dark blue boxes; n = 102 cells; median L-ratio 0.06 (25th–75th percentiles 0.02–0.19); median isolation distance 31.2 (18.0–49.7)), and all with two or three fields (light grey boxes; n = 60 cells; median L-ratio 0.06 (0.02–0.14); median isolation distance 31.7 (21.4–49.2)). Black line between box edges indicates median, box edges indicate 25th and 75th percentiles, whiskers extend to the most extreme point that lies within 1.5 × IQR, and data points larger than 1.5 × IQR are considered outliers (red crosses).
Extended Data Fig. 6 Object-vector cells are allocentric.
a, Egocentric reference frame with 0° defined as moving towards the object (white circle) and 180° as moving away from the object. b, Left, colour-coded firing rate map for a representative object-vector cell (peak rate below rate map; mouse and cell ID numbers indicated in vertical text bar). Right, path plot showing, for the same cell as in the rate map, the mouse’s path with overlaid spike locations in black. Left path plot shows spikes on trajectories away from the object; right plot shows spikes on trajectories towards the object. c, Egocentric directional tuning curve for the cell in b. Firing rate is shown as a function of direction of movement relative to the object. Directional bins were 20°. Note that egocentric directional modulation is nearly absent. d, Colour-coded egocentric directional tuning curves (as in c) for all object-vector cells. Each horizontal line corresponds to one cell and shows firing rate, colour-coded as a function of movement direction. Cells are sorted according to the movement direction that had the highest firing rate (light yellow). Note the relative absence of egocentric directional tuning. e, Distribution of egocentric directional modulation across the entire sample of object-vector cells. Egocentric directional modulation was estimated by defining for each cell an egocentric directionality index as the mean vector length of the egocentric tuning curve. Distribution of observed values for object-vector cells is shown in blue, shuffled data in grey. Red line marks the 99th percentile of egocentric directional modulation values for the shuffled data. Only ten object-vector cells had egocentric modulation that exceeded the 99th percentile.
Extended Data Fig. 7 Orientation of object-vector fields is independent of the geometry of the environment but breaks down in the absence of visual input.
a–c, Experiment in which eight cells from three mice were recorded successively in a circular and a square recording box. The boxes were placed at the same location in the recording room and cues external to the box were identical. a, Left, colour-coded rate maps of three cells recorded first in the circle, then in the square. Peak rates are indicated below the rate maps, mouse and cell ID numbers to the left. Colour bar indicates normalized firing rate. Right, directional tuning curves for the same three cells, with firing rates shown as a function of allocentric direction relative to the object. b, Correlation between directional tuning curves in square and circular environments for all eight cells. Black line between box edges indicates median, box edges indicate 25th and 75th percentiles, whiskers extend to the most extreme point that lies within 1.5 × IQR. c, Difference in peak direction of tuning curves between square and circle for all eight cells. d–f, Object-vector cells recorded in light and in complete darkness. d, Colour-coded firing rate maps from five example cells recorded successively in light and darkness (top and bottom, respectively). Mouse and cell ID numbers are shown at the top of each column, peak rates below each rate map. Colour scale is similar for each column of rate maps. e, Distribution of vector-map correlations across pairs of trials recorded either successively in light (yellow) or first in light and then in darkness (grey; n = 21 cells). Stippled line marks the 99th percentile correlation threshold. f, Distributions of spatial information content, spatial coherence, peak firing rate and mean firing rate in light and in darkness. All four measures decreased from light to darkness (spatial information content: Wilcoxon signed-rank test, W = 227, n = 21, P = 1.1 × 10−4; spatial coherence: W = 231, n = 21, P = 6.0 × 10−5; peak firing rate: W = 230, n = 21, P = 6.9 × 10−5; mean firing rate: W = 212, n1 = n2 = 95, P = 8.0 × 10−4). All statistical tests were two-sided. g, Distribution of head-direction scores of all object-vector cells recorded in light and in darkness. Head-direction tuning increased significantly in the absence of visual cues (two-sided Wilcoxon signed rank test: W = 36, n = 21, P = 0.005).
Extended Data Fig. 8 Intersection with grid cells, head-direction cells and boundary-vector cells.
a, Colour-coded rate maps showing 12 representative grid cells recorded in the absence (left) and presence (right) of objects on consecutive trials. Mouse and cell ID numbers are indicated to the left of each pair of columns; grid score (G.s.) and peak rate are shown below each rate map. Scale bar indicates firing rate. Cells in the top three rows of the left pair of columns are examples of grid cells that expressed an extra field in the vicinity of at least one of the objects. Such effects were observed in 10 out of 124 grid cells. Only four grid cells passed the criteria for object-vector cells. Grid fields from the no-object trial mostly retained their firing locations when the object was added, but in a few cases single fields were moderately displaced or the grid underwent mild disruption. b, Colour-coded rate maps and head-direction tuning curves for six representative head-direction cells recorded with no object (left) and with an object (right) on consecutive trials. Mouse and cell ID numbers are indicated to the left; peak rate is shown below each rate map and head-direction score and peak rate are shown below each head-direction tuning curve. Sharply tuned head-direction cells mostly failed to develop vector fields in the presence of objects (exemplified by the cells in the top three rows). One of the few object-vector cells that also had sharp head-direction tuning is cell 398 in the fourth row. The majority of object-vector cells that passed as head-direction cells had only moderate head-direction tuning, and this tuning was clearly reduced when the object was introduced (Extended Data Fig. 4c, d and exemplified by cells 351 and 266 in the two bottom rows of this panel). c, Colour-coded rate maps for all cells that pass a criterion for boundary-vector cells. Symbols as in a. Twenty out of 840 cells passed the criterion for boundary-vector cells. Among these, only one had a firing field that did not encroach upon the wall (mouse 80569, cell 524, highlighted in square frame). d, Distance between boundary and centre of boundary-vector firing field (n = 20 fields from 20 cells) for all cells that passed the criterion for boundary-vector cells, compared to distance between nearest point of object and centre of object-vector fields (n = 221 object-vector fields from 162 cells). Black line between box edges indicates median, box edges indicate 25th and 75th percentiles, whiskers extend to the most extreme point that lies within 1.5 × IQR, and data points larger than 1.5 × IQR are considered outliers (red crosses). The distribution of distances in object-vector fields is skewed towards greater distances than the distribution of distances in boundary-vector fields (two-sided Mann–Whitney U-test, U = 703, P = 9.0 × 10−9).
Extended Data Fig. 9 Rate maps from all recordings with stepwise increases in length, diameter or height of the object.
a, Colour-coded firing rate maps of all 24 cells recorded in experiments in which objects were elongated in one dimension. Each row of four rate maps shows one cell. The four maps are scaled to the same maximum rate (common colour scale). Mouse and cell ID numbers are indicated to the left of each row. Fifteen cells were recorded while the length of the object was increased in steps from 6.75 cm to 62.5 cm. Nine cells were recorded while the length of the object was changed in the opposite direction, from 62.5 cm to 6.75 cm (cells indicated by arrows to the right). For some cells (for example, cells 862 and 927), firing fields increased in length as the object was extended; for other cells (for example, cells 1079 and 1042), the fields retain similar sizes and shapes across the entire spectrum of object lengths. b, Rate maps showing object-vector cell in experiment with no gap between internal and external walls (middle, right). c, Firing rate maps of 6 out of 23 cells recorded in experiments in which the diameter of a cylindrical object was increased from 2 cm to 20 cm. Note persistence of firing fields with increasing diameter of the object. Scale bar indicates colour-coded firing rate. d, Firing rate maps of 7 out of 21 cells recorded in experiments in which the height of prismatic object was increased from 2 cm to 40 cm. Colour-coded firing rate is indicated by scale bar.
Extended Data Fig. 10 Distinction between object-vector cells and border cells.
a, Experiment with object on suspended wall. Image to the left shows recording box with an object attached to a suspended wall with a 15-cm passage underneath the wall and the object. In this configuration, there is no impediment to the mouse’s movement near the object. Right, colour-coded rate maps for three example object-vector cells recorded on trials without any objects present (top row) and with an object (black square) attached to a suspended wall (white line). The three cells respond robustly to the suspended object. b, Colour-coded firing rate maps of four border cells recorded in the absence or presence of an object. The two cells on the left (one in a square and one in a circular box) showed no response to the object. The two cells on the right produced clear object-vector fields. c, Overlap between populations of object-vector cells and border cells (BCs). Fifteen out of 56 border cells also passed the criteria for object-vector cells. The two cells to the right in b are among those cells. d, Box plot showing, for the 15 overlapping border and object-vector cells, the distance from centres of object-vector fields to the nearest point of the object, and the distance from centres of border fields to the nearest wall. Black line between box edges indicates median, box edges indicate 25th and 75th percentiles, whiskers extend to the most extreme point that lies within 1.5 × IQR. Mean distance from object-vector field to object was significantly greater than the distance from border field to the wall (object-vector field to object: 21.4 ± 2.6 cm; border field to wall: 7.6 ± 0.6 cm; two-sided Mann–Whitney U-test, U = 381, P = 1.6 × 10−4), consistent with the interpretation that border cells and object-vector cells are functionally independent (Fig. 4).
Supplementary information
Supplementary Information
This file contains additional results as well as discussion and comparison to previous literature.
Source data
Rights and permissions
About this article
Cite this article
Høydal, Ø.A., Skytøen, E.R., Andersson, S.O. et al. Object-vector coding in the medial entorhinal cortex. Nature 568, 400–404 (2019). https://doi.org/10.1038/s41586-019-1077-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1077-7
This article is cited by
-
Converting an allocentric goal into an egocentric steering signal
Nature (2024)
-
A consistent map in the medial entorhinal cortex supports spatial memory
Nature Communications (2024)
-
Environment geometry alters subiculum boundary vector cell receptive fields in adulthood and early development
Nature Communications (2024)
-
Subicular neurons encode concave and convex geometries
Nature (2024)
-
Reinforcement Learning Navigation for Robots Based on Hippocampus Episode Cognition
Journal of Bionic Engineering (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.