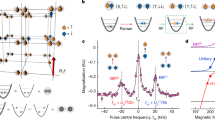
Abstract
In high-energy and condensed-matter physics, particle exchange has an essential role in the understanding of long-range interactions and correlations. For example, the exchange of massive bosons leads to the Yukawa potential1,2, and phonon exchange between electrons gives rise to Cooper pairing in superconductors3. Here we show that, when a Bose–Einstein condensate of caesium atoms is embedded in a degenerate Fermi gas of lithium atoms, interspecies interactions can give rise to an effective trapping potential, damping, and attractive boson–boson interactions mediated by fermions. The latter, which is related to the Ruderman–Kittel–Kasuya–Yosida mechanism4, results from a coherent three-body scattering process. Such mediated interactions are expected to form new magnetic phases5 and supersolids6. We show that under suitable conditions, the mediated interactions can convert a stable Bose–Einstein condensate into a train of ‘Bose–Fermi solitons’7,8. The predicted long-range nature of the mediated interactions opens up the possibility of correlating distant atoms and preparing new quantum phases.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Yukawa, H. On the interaction of elementary particles. I. Proc. Phys.-Math. Soc. Jpn 3rd Ser. 17, 48–57 (1935).
Yukawa, H. & Sakata, S. On the interaction of elementary particles. II. Proc. Phys.-Math. Soc. Jpn 3rd Ser. 19, 1084–1093 (1937).
Tinkham, M. Introduction to Superconductivity (McGraw-Hill, 1975).
Ruderman, M. A. & Kittel, C. Indirect exchange coupling of nuclear magnetic moments by conduction electrons. Phys. Rev. 96, 99–102 (1954).
De, S. & Spielman, I. B. Fermion-mediated long-range interactions between bosons stored in an optical lattice. Appl. Phys. B 114, 527–536 (2014).
Büchler, H. P. & Blatter, G. Supersolid versus phase separation in atomic Bose–Fermi mixtures. Phys. Rev. Lett. 91, 130404 (2003).
Karpiuk, T. et al. Soliton trains in Bose–Fermi mixtures. Phys. Rev. Lett. 93, 100401 (2004).
Santhanam, J., Kenkre, V. M. & Konotop, V. V. Solitons of Bose–Fermi mixtures in a strongly elongated trap. Phys. Rev. A 73, 013612 (2006).
Lu, M., Burdick, N. Q., Youn, S. H. & Lev, B. L. Strongly dipolar Bose–Einstein condensate of dysprosium. Phys. Rev. Lett. 107, 190401 (2011).
Balewski, J. B. et al. Coupling a single electron to a Bose–Einstein condensate. Nature 502, 664–667 (2013).
Ni, K.-K. et al. A high phase-space-density gas of polar molecules. Science 322, 231–235 (2008).
Ferrier-Barbut, I., Kadau, H., Schmitt, M., Wenzel, M. & Pfau, T. Observation of quantum droplets in a strongly dipolar Bose gas. Phys. Rev. Lett. 116, 215301 (2016).
Chomaz, L. et al. Quantum-fluctuation-driven crossover from a dilute Bose–Einstein condensate to a macrodroplet in a dipolar quantum fluid. Phys. Rev. X 6, 041039 (2016).
Hazzard, K. R. A. et al. Many-body dynamics of dipolar molecules in an optical lattice. Phys. Rev. Lett. 113, 195302 (2014).
Guardado-Sanchez, E. et al. Probing the quench dynamics of antiferromagnetic correlations in a 2D quantum Ising spin system. Phys. Rev. X 8, 021069 (2018).
Zeiher, J. et al. Many-body interferometry of a Rydberg-dressed spin lattice. Nat. Phys. 12, 1095–1099 (2016).
Suchet, D., Wu, Z., Chevy, F. & Bruun, G. M. Long-range mediated interactions in a mixed-dimensional system. Phys. Rev. A 95, 043643 (2017).
Tsurumi, T. & Wadati, M. Dynamics of magnetically trapped boson–fermion mixtures. J. Phys. Soc. Jpn 69, 97–103 (2000).
Chui, S. T. & Ryzhov, V. N. Collapse transition in mixtures of bosons and fermions. Phys. Rev. A 69, 043607 (2004).
Santamore, D. H. & Timmermans, E. Fermion-mediated interactions in a dilute Bose–Einstein condensate. Phys. Rev. A 78, 013619 (2008).
Berninger, M. et al. Feshbach resonances, weakly bound molecular states, and coupled-channel potentials for cesium at high magnetic fields. Phys. Rev. A 87, 032517 (2013).
Tung, S. K. et al. Ultracold mixtures of atomic 6Li and 133Cs with tunable interactions. Phys. Rev. A 87, 010702(R) (2013).
Johansen, J., DeSalvo, B. J., Patel, K. & Chin, C. Testing universality of Efimov physics across broad and narrow Feshbach resonances. Nat. Phys. 13, 731–735 (2017).
DeSalvo, B. J., Patel, K., Johansen, J. & Chin, C. Observation of a degenerate Fermi gas trapped by a Bose–Einstein condensate. Phys. Rev. Lett. 119, 233401 (2017).
Ferlaino, F. et al. Dipolar oscillations in a quantum degenerate Fermi–Bose atomic mixture. J. Opt. B 5, S3 (2003).
Ferrier-Barbut, I. et al. A mixture of Bose and Fermi superfluids. Science 345, 1035–1038 (2014).
Roy, R., Green, A., Bowler, R. & Gupta, S. Two-element mixture of Bose and Fermi superfluids. Phys. Rev. Lett. 118, 055301 (2017).
Gensemer, S. D. & Jin, D. S. Transition from collisionless to hydrodynamic behavior in an ultracold Fermi gas. Phys. Rev. Lett. 87, 173201 (2001).
Ferrari, G. et al. Collisional properties of ultracold K–Rb mixtures. Phys. Rev. Lett. 89, 053202 (2002).
Lous, R. S. et al. Probing the interface of a phase-separated state in a repulsive Bose–Fermi mixture. Phys. Rev. Lett. 120, 243403 (2018).
Dalfovo, F., Giorgini, S., Pitaevskii, L. P. & Stringari, S. Theory of Bose–Einstein condensation in trapped gases. Rev. Mod. Phys. 71, 463–512 (1999).
Leo, P. J., Williams, C. J. & Julienne, P. S. Collision properties of ultracold 133Cs atoms. Phys. Rev. Lett. 85, 2721–2724 (2000).
Acknowledgements
We thank M. Gajda for discussions and M. McDonald for a careful reading of the manuscript. This work was supported by National Science Foundation (NSF) grant no. PHY-1511696 and the University of Chicago Materials Research Science and Engineering Center, which is funded by the NSF under grant no. DMR-1420709.
Reviewer information
Nature thanks Georg Bruun and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
B.J.D., K.P. and C.C. designed the experiment. K.P. and G.C. collected the data. B.J.D., K.P. and G.C. analysed the data. B.J.D. wrote the manuscript and all authors contributed to the final version.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Caesium–caesium and lithium–caesium scattering lengths over the studied magnetic field range.
The caesium–caesium scattering length aBB is shown with a blue line, and the lithium–caesium scattering length aBF with a red line. The interspecies Feshbach resonance near B = 892 G is used for sample preparation and the effective trapping frequency measurements, indicated by the light green shaded area. The caesium–caesium zero crossing near B = 880 G is used for the effective scattering length measurements, indicated by the blue shaded area. In this region, the lithium–caesium scattering length is nearly constant at aBF = −60a0 (ref. 22).
Extended Data Fig. 2 Raw data for measurement of the difference in scattering length.
Top, Measured radius of the caesium BEC with (red circles) and without (blue circles) lithium. Bottom, Measured BEC number with (red circles) and without (blue circles) lithium. At every field, the size of the BEC with lithium present is smaller than the corresponding measurement without lithium. However, overall experimental drift makes absolute comparison difficult. Calibrating each measurement point-by-point as described enables us to extract the difference in scattering length cleanly, as can be seen in Fig. 3b. Error bars are calculated as the standard error of the mean from multiple measurements.
Rights and permissions
About this article
Cite this article
DeSalvo, B.J., Patel, K., Cai, G. et al. Observation of fermion-mediated interactions between bosonic atoms. Nature 568, 61–64 (2019). https://doi.org/10.1038/s41586-019-1055-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1055-0
This article is cited by
-
Mediated interactions between Fermi polarons and the role of impurity quantum statistics
Nature Physics (2024)
-
Modelling quantum aspects of disruption of a white dwarf star by a black hole
Scientific Reports (2021)
-
Effective p-wave Fermi-Fermi Interaction Induced by Bosonic Superfluids
Scientific Reports (2020)
-
New interactions seen in an ultracold gas
Nature (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.