Abstract
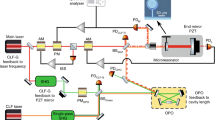
Quantum mechanics places a fundamental limit on the precision of continuous measurements. The Heisenberg uncertainty principle dictates that as the precision of a measurement of an observable (for example, position) increases, back action creates increased uncertainty in the conjugate variable (for example, momentum). In interferometric gravitational-wave detectors, higher laser powers reduce the position uncertainty created by shot noise (the photon-counting error caused by the quantum nature of the laser) but necessarily do so at the expense of back action in the form of quantum radiation pressure noise (QRPN)1. Once at design sensitivity, the gravitational-wave detectors Advanced LIGO2, VIRGO3 and KAGRA4 will be limited by QRPN at frequencies between 10 hertz and 100 hertz. There exist several proposals to improve the sensitivity of gravitational-wave detectors by mitigating QRPN5,6,7,8,9,10, but until now no platform has allowed for experimental tests of these ideas. Here we present a broadband measurement of QRPN at room temperature at frequencies relevant to gravitational-wave detectors. The noise spectrum obtained shows effects due to QRPN between about 2 kilohertz and 100 kilohertz, and the measured magnitude of QRPN agrees with our model. We now have a testbed for studying techniques with which to mitigate quantum back action, such as variational readout and squeezed light injection7, with the aim of improving the sensitivity of future gravitational-wave detectors.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
The data pertaining to this study are available from the corresponding authors upon reasonable request.
References
Caves, C. M. Quantum-mechanical radiation-pressure fluctuations in an interferometer. Phys. Rev. Lett. 45, 75–79 (1980).
The LIGO Scientific Collaboration. Advanced LIGO. Class. Quantum Gravity 32, 074001 (2015).
Acernese, F. et al. Advanced Virgo: a second-generation interferometric gravitational wave detector. Class. Quantum Gravity 32, 024001 (2015).
Somiya, K. Detector configuration of KAGRA–the Japanese cryogenic gravitational-wave detector. Class. Quantum Gravity 29, 124007 (2012).
Braginsky, V. B., Vorontsov, Y. I. & Thorne, K. S. Quantum nondemolition measurements. Science 209, 547–557 (1980).
Braginsky, V. B., Gorodetsky, M. L., Khalili, F. Y. & Thorne, K. S. Dual-resonator speed meter for a free test mass. Phys. Rev. D 61, 044002 (2000).
Kimble, H. J., Levin, Y., Matsko, A. B., Thorne, K. S. & Vyatchanin, S. P. Conversion of conventional gravitational-wave interferometers into quantum nondemolition interferometers by modifying their input and/or output optics. Phys. Rev. D 65, 022002 (2001).
Harms, J. et al. Squeezed-input, optical-spring, signal-recycled gravitational-wave detectors. Phys. Rev. D 68, 042001 (2003).
Oelker, E. et al. Audio-band frequency-dependent squeezing for gravitational-wave detectors. Phys. Rev. Lett. 116, 041102 (2016).
Gräf, C. et al. Design of a speed meter interferometer proof-of-principle experiment. Class. Quantum Gravity 31, 215009 (2014).
Braginsky, V. B. & Manukin, A. B. Measurement of Weak Forces in Physics Experiments (Univ. Chicago Press, Chicago, 1977).
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981).
Saulson, P. R. Thermal noise in mechanical experiments. Phys. Rev. D 42, 2437–2445 (1990).
Purdy, T. P., Peterson, R. W. & Regal, C. A. Observation of radiation pressure shot noise on a macroscopic object. Science 339, 801–804 (2013).
Teufel, J. D., Lecocq, F. & Simmonds, R. W. Overwhelming thermomechanical motion with microwave radiation pressure shot noise. Phys. Rev. Lett. 116, 013602 (2016).
Purdy, T. P., Grutter, K. E., Srinivasan, K. & Taylor, J. M. Quantum correlations from a room-temperature optomechanical cavity. Science 356, 1265–1268 (2017).
Sudhir, V. et al. Quantum correlations of light from a room-temperature mechanical oscillator. Phys. Rev. X 7, 031055 (2017).
Cole, G. D., Gröblacher, S., Gugler, K., Gigan, S. & Aspelmeyer, M. Monocrystalline AlxGa1-xAs heterostructures for high-reflectivity high-Q micromechanical resonators in the megahertz regime. Appl. Phys. Lett. 92, 261108 (2008).
Cole, G. D. Cavity optomechanics with low-noise crystalline mirrors. Proc. SPIE 8458, 845807 (2012).
Cole, G. D. et al. High-performance near- and mid-infrared crystalline coatings. Optica 3, 647–656 (2016).
Singh, R., Cole, G. D., Cripe, J. & Corbitt, T. Stable optical trap from a single optical field utilizing birefringence. Phys. Rev. Lett. 117, 213604 (2016).
Cripe, J. et al. Radiation-pressure-mediated control of an optomechanical cavity. Phys. Rev. A 97, 013827 (2018).
Nyquist, H. Thermal agitation of electric charge in conductors. Phys. Rev. 32, 110–113 (1928).
Fedorov, S. et al. Evidence for structural damping in a high-stress silicon nitride nanobeam and its implications for quantum optomechanics. Phys. Lett. A 382, 2251–2255 (2018).
Corbitt, T., Chen, Y. & Mavalvala, N. Mathematical framework for simulation of quantum fields in complex interferometers using the two-photon formalism. Phys. Rev. A 72, 013818 (2005).
Corbitt, T. et al. Squeezed-state source using radiation-pressure-induced rigidity. Phys. Rev. A 73, 023801 (2006).
Willke, B., Brozek, S., Danzmann, K., Quetschke, V. & Gossler, S. Frequency stabilization of a monolithic Nd:YAG ring laser by controlling the power of the laser-diode pump source. Opt. Lett. 25, 1019–1021 (2000).
Braginsky, V., Gorodetsky, M. & Vyatchanin, S. Thermodynamical fluctuations and photo-thermal shot noise in gravitational wave antennae. Phys. Lett. A 264, 1–10 (1999).
Aggarwal, N. et al. Room temperature optomechanical squeezing. Preprint at http://arXiv.org/abs/1812.09942 (2018).
Cripe, J. et al. Quantum back action cancellation in the audio band. Preprint at http://arXiv.org/abs/1812.10028 (2018).
Yap, M. J. et al. Broadband reduction of quantum radiation pressure noise via squeezed light injection. Preprint at http://arXiv.org/abs/1812.09804 (2018).
Corbitt, T. et al. An all-optical trap for a gram-scale mirror. Phys. Rev. Lett. 98, 150802 (2007).
Aspelmeyer, M., Kippenberg, T. J. & Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 86, 1391–1452 (2014).
Acknowledgements
J.C. and T.C. are supported by National Science Foundation grants PHY-1150531 and PHY-1806634. N.A., A.L. and N.M. are supported by National Science Foundation grants PHY-1707840 and PHY-1404245. A portion of this work was performed in the UCSB Nanofabrication Facility. J.C. and T.C. thank D. McClelland, R. Ward and M. J. Yap for comments and discussion. The authors thank C. Wipf and V. Sudhir for comments during the manuscript preparation. This document has been assigned the LIGO document number LIGO-P1800033.
Reviewer information
Nature thanks Warwick Bowen, Yuta Michimura and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
J.C. led the design, construction and data taking for the experiment, and prepared the manuscript. T.C. supervised the design and construction of the experiment, and also helped with the data taking and analysis of the results. N.A., R.L., A.L. and N.M. contributed to the design of the microresonators and the writing of the manuscript. G.D.C. provided feedback on the design of the microresonators and, together with P.H. and D.F., fabricated the devices. R.S. contributed experience from previous experiments.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Full noise budget.
For the measurement with 220 mW circulating power, each noise source that contributed to the sum of subdominant noises in Fig. 2 is shown (see key). The narrow peaks in the displacement noise measurement are a result of parametric nonlinear coupling between various mechanical modes, and this coupling is negligible at low circulating powers.
Extended Data Fig. 2 Dependence of thermal noise on circulating power as caused by change in beam position.
a, The total displacement noise around the yaw mechanical mode for each of the four circulating power levels (see key). b, As a but centred on the pitch mechanical mode. In these measurements, thermal noise is the dominant noise source at frequencies near the mechanical resonances. The thermal noise around the pitch mode decreases from 73 mW to 110 mW of circulating power, and then increases at 220 mW. This change is consistent with the cavity mode passing through the nodal point of this mode at an intermediate power level. Each panel includes an image from the finite element model depicting the motion associated with the mechanical mode. In both images, the blue portion represents a positive displacement from equilibrium (thin black outline), and the red area denotes a negative displacement. The nodal line for the mechanical modes is drawn in white.
Extended Data Fig. 3 Comparison of thermal noise spectra at different alignments.
The effect of the change in beam position is seen in the change of height of the peaks in the displacement spectrum at the frequencies of the higher-order mechanical modes. The blue curve is taken with 10 mW of circulating power with a cavity mode alignment similar to the QRPN measurement with 220 mW circulating power. The green curve is for an alignment to minimize the coupling of the pitch and yaw modes at 10 mW circulating power. The red curve is based on a model that sets the modal mass of the higher-order modes so that the peaks match those in the displacement measurement shown in Fig. 2.
Extended Data Fig. 4 Effect of uncertainty in detuning and loss.
Modelled quantum displacement noise at 20 kHz and 220 mW of circulating power is shown as a function of intracavity loss and cavity detuning: the optical-spring frequency, which has been precisely measured, is held constant in the model. To be conservative, the range in values for the cavity loss and detuning in this figure are much larger than the constraints obtained by measurements of the optical spring.
Extended Data Fig. 5 QRPN as a function of frequency and power.
This contour plot shows what fraction of the total measured displacement noise power spectral density (PSD) is contributed by QRPN, as a function of measurement frequency and circulating power. The quantity shown on the colour scale at right is the ratio of the PSDs of the QRPN model to the total measured noise. Whereas in the rest of this Letter we present the data as amplitude spectral densities in order to put them in the perspective of GW measurements, we use PSDs to calculate percentage and ratios, and to make this figure, because all the noises are added in quadrature to make up the total noise. We interpolate the data between the measurements at 73 mW, 110 mW, 150 mW and 220 mW. The vertical stripe at 876 Hz is an artefact of the fundamental resonance not being perfectly resolved in the measurement. The blue vertical stripes at 3.7 kHz, 15 kHz and 28 kHz are higher-order mechanical modes of the microresonator. The contours are at a spacing of 0.05 (5%).
Extended Data Fig. 6 Projected QRPN.
Shown is the measured QRPN level obtained by multiplying the transfer function measurement TFAM by the shot noise of the effective cavity input power and applying the calibration procedure, as described in Methods. The result of this calculation agrees with the modelled QRPN.
Rights and permissions
About this article
Cite this article
Cripe, J., Aggarwal, N., Lanza, R. et al. Measurement of quantum back action in the audio band at room temperature. Nature 568, 364–367 (2019). https://doi.org/10.1038/s41586-019-1051-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-1051-4
This article is cited by
-
Room-temperature quantum optomechanics using an ultralow noise cavity
Nature (2024)
-
Acoustic frequency atomic spin oscillator in the quantum regime
Nature Communications (2023)
-
Optomechanics for quantum technologies
Nature Physics (2022)
-
Nonlinearity-mediated digitization and amplification in electromechanical phonon-cavity systems
Nature Communications (2022)
-
Strained crystalline nanomechanical resonators with quality factors above 10 billion
Nature Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.