Abstract
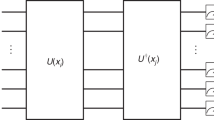
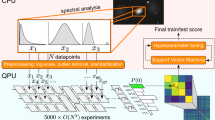
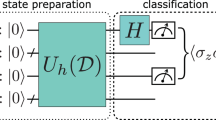
Machine learning and quantum computing are two technologies that each have the potential to alter how computation is performed to address previously untenable problems. Kernel methods for machine learning are ubiquitous in pattern recognition, with support vector machines (SVMs) being the best known method for classification problems. However, there are limitations to the successful solution to such classification problems when the feature space becomes large, and the kernel functions become computationally expensive to estimate. A core element in the computational speed-ups enabled by quantum algorithms is the exploitation of an exponentially large quantum state space through controllable entanglement and interference. Here we propose and experimentally implement two quantum algorithms on a superconducting processor. A key component in both methods is the use of the quantum state space as feature space. The use of a quantum-enhanced feature space that is only efficiently accessible on a quantum computer provides a possible path to quantum advantage. The algorithms solve a problem of supervised learning: the construction of a classifier. One method, the quantum variational classifier, uses a variational quantum circuit1,2 to classify the data in a way similar to the method of conventional SVMs. The other method, a quantum kernel estimator, estimates the kernel function on the quantum computer and optimizes a classical SVM. The two methods provide tools for exploring the applications of noisy intermediate-scale quantum computers3 to machine learning.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
All data generated or analysed during this study are included in this Letter (and its Supplementary Information).
References
Mitarai, K., Negoro, M., Kitagawa, M. & Fujii, K. Quantum circuit learning. Preprint at https://arxiv.org/abs/1803.00745 (2018).
Farhi, E. & Neven, H. Classification with quantum neural networks on near term processors. Preprint at https://arxiv.org/abs/1802.06002 (2018).
Preskill, J. Quantum computing in the NISQ era and beyond. Preprint at https://arxiv.org/abs/1801.00862 (2018).
Arunachalam, S. & de Wolf, R. Guest column: a survey of quantum learning theory. SIGACT News 48, 41–67 (2017).
Ciliberto, C. et al. Quantum machine learning: a classical perspective. Proc. R. Soc. Lond. A 474, 20170551 (2018).
Dunjko, V. & Briegel, H. J. Machine learning & artificial intelligence in the quantum domain: a review of recent progress. Rep. Prog. Phys. 81, 074001 (2018).
Biamonte, J. et al. Quantum machine learning. Nature 549, 195–202 (2017).
Romero, J., Olson, J. P. & Aspuru-Guzik, A. Quantum autoencoders for efficient compression of quantum data. Quant. Sci. Technol. 2, 045001 (2017).
Wan, K. H., Dahlsten, O., Kristjánsson, H., Gardner, R. & Kim, M. Quantum generalisation of feedforward neural networks. Preprint at https://arxiv.org/abs/1612.01045 (2016).
Temme, K., Bravyi, S. & Gambetta, J. M. Error mitigation for short-depth quantum circuits. Phys. Rev. Lett. 119, 180509 (2017).
Li, Y. & Benjamin, S. C. Efficient variational quantum simulator incorporating active error minimization. Phys. Rev. X 7, 021050 (2017).
Terhal, B. M. & DiVincenzo, D. P. Adaptive quantum computation, constant depth quantum circuits and Arthur-Merlin games. Quantum Inf. Comput. 4, 134–145 (2004).
Bremner, M. J., Montanaro, A. & Shepherd, D. J. Achieving quantum supremacy with sparse and noisy commuting quantum computations. Quantum 1, 8 (2017).
Vapnik, V. The Nature of Statistical Learning Theory (Springer Science & Business Media, 2013).
Rebentrost, P., Mohseni, M. & Lloyd, S. Quantum support vector machine for big data classification. Phys. Rev. Lett. 113, 130503 (2014).
Kandala, A. et al. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature 549, 242–246 (2017).
Farhi, E., Goldstone, J., Gutmann, S. & Neven, H. Quantum algorithms for fixed qubit architectures. Preprint at https://arxiv.org/abs/1703.06199 (2017).
Burges, C. J. A tutorial on support vector machines for pattern recognition. Data Min. Knowl. Discov. 2, 121–167 (1998).
Boser, B. E., Guyon, I. M. & Vapnik, V. N. A training algorithm for optimal margin classifiers. In Proc. 5th Annual Workshop on Computational Learning Theory 144–152 (ACM, 1992).
Goldberg, L. A. & Guo, H. The complexity of approximating complex-valued Ising and Tutte partition functions. Computat. Complex. 26, 765–833 (2017).
Demarie, T. F., Ouyang, Y. & Fitzsimons, J. F. Classical verification of quantum circuits containing few basis changes. Phys. Rev. A 97, 042319 (2018).
Spall, J. C. A one-measurement form of simultaneous perturbation stochastic approximation. Automatica 33, 109–112 (1997).
Spall, J. C. Adaptive stochastic approximation by the simultaneous perturbation method. IEEE Trans. Automat. Contr. 45, 1839 (2000).
Kandala, A. et al. Extending the computational reach of a noisy superconducting quantum processor. Preprint at https://arxiv.org/abs/1805.04492 (2018).
Buhrman, H., Cleve, R., Watrous, J. & De Wolf, R. Quantum fingerprinting. Phys. Rev. Lett. 87, 167902 (2001).
Cincio, L., Subas, Y., Sornborger, A. T. & Coles, P. J. Learning the quantum algorithm for state overlap. Preprint at https://arxiv.org/abs/1803.04114 (2018).
Smolin, J. A., Gambetta, J. M. & Smith, G. Efficient method for computing the maximum-likelihood quantum state from measurements with additive Gaussian noise. Phys. Rev. Lett. 108, 070502 (2012).
Schuld, M. & Killoran, N. Quantum machine learning in feature Hilbert spaces. Preprint at https://arxiv.org/abs/1803.07128 (2018).
Schuld, M., Bocharov, A., Svore, K. & Wiebe, N. Circuit-centric quantum classifiers. Preprint at https://arxiv.org/abs/1804.00633 (2018).
Acknowledgements
We thank S. Bravyi for discussions. A.W.H. acknowledges funding from the MIT-IBM Watson AI Lab under the project ‘Machine Learning in Hilbert Space’. The research was supported by the IBM Research Frontiers Institute. We acknowledge support from IARPA under contract W911NF-10-1-0324 for device fabrication.
Reviewer information
Nature thanks Christopher Eichler, Seth Lloyd, Maria Schuld and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
The work on the classifier theory was led by V.H. and K.T. The experiment was designed by A.D.C., J.M.G. and K.T. and implemented by A.D.C. All authors contributed to the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare competing interests: Elements of this work are included in a patent filed by the International Business Machines Corporation with the US Patent and Trademark office.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains supplementary text I–IX and references and includes Figs.1–9 and Tables I–II.
Supplementary Data
This file contains Supplementary Data tables.
Rights and permissions
About this article
Cite this article
Havlíček, V., Córcoles, A.D., Temme, K. et al. Supervised learning with quantum-enhanced feature spaces. Nature 567, 209–212 (2019). https://doi.org/10.1038/s41586-019-0980-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-0980-2
This article is cited by
-
Covariant quantum kernels for data with group structure
Nature Physics (2024)
-
A framework for demonstrating practical quantum advantage: comparing quantum against classical generative models
Communications Physics (2024)
-
Towards provably efficient quantum algorithms for large-scale machine-learning models
Nature Communications (2024)
-
Quantum discriminator for binary classification
Scientific Reports (2024)
-
Understanding quantum machine learning also requires rethinking generalization
Nature Communications (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.