Abstract
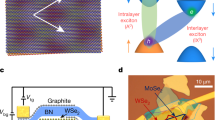
The formation of moiré patterns in crystalline solids can be used to manipulate their electronic properties, which are fundamentally influenced by periodic potential landscapes. In two-dimensional materials, a moiré pattern with a superlattice potential can be formed by vertically stacking two layered materials with a twist and/or a difference in lattice constant. This approach has led to electronic phenomena including the fractal quantum Hall effect1,2,3, tunable Mott insulators4,5 and unconventional superconductivity6. In addition, theory predicts that notable effects on optical excitations could result from a moiré potential in two-dimensional valley semiconductors7,8,9, but these signatures have not been detected experimentally. Here we report experimental evidence of interlayer valley excitons trapped in a moiré potential in molybdenum diselenide (MoSe2)/tungsten diselenide (WSe2) heterobilayers. At low temperatures, we observe photoluminescence close to the free interlayer exciton energy but with linewidths over one hundred times narrower (around 100 microelectronvolts). The emitter g-factors are homogeneous across the same sample and take only two values, −15.9 and 6.7, in samples with approximate twist angles of 60 degrees and 0 degrees, respectively. The g-factors match those of the free interlayer exciton, which is determined by one of two possible valley-pairing configurations. At twist angles of approximately 20 degrees the emitters become two orders of magnitude dimmer; however, they possess the same g-factor as the heterobilayer at a twist angle of approximately 60 degrees. This is consistent with the umklapp recombination of interlayer excitons near the commensurate 21.8-degree twist angle7. The emitters exhibit strong circular polarization of the same helicity for a given twist angle, which suggests that the trapping potential retains three-fold rotational symmetry. Together with a characteristic dependence on power and excitation energy, these results suggest that the origin of the observed effects is interlayer excitons trapped in a smooth moiré potential with inherited valley-contrasting physics. This work presents opportunities to control two-dimensional moiré optics through variation of the twist angle.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Dean, C. R. et al. Hofstadter’s butterfly and the fractal quantum Hall effect in moiré superlattices. Nature 497, 598–602 (2013).
Hunt, B. et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure. Science 340, 1427–1430 (2013).
Ponomarenko, L. A. et al. Cloning of Dirac fermions in graphene superlattices. Nature 497, 594–597 (2013).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. https://doi.org/10.1038/s41567-018-0387-2 (2019).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Yu, H., Wang, Y., Tong, Q., Xu, X. & Yao, W. Anomalous light cones and valley optical selection rules of interlayer excitons in twisted heterobilayers. Phys. Rev. Lett. 115, 187002 (2015).
Yu, H., Liu, G.-B., Tang, J., Xu, X. & Yao, W. Moiré excitons: From programmable quantum emitter arrays to spin-orbit–coupled artificial lattices. Sci. Adv. 3, e1701696 (2017).
Wu, F., Lovorn, T. & MacDonald, A. H. Theory of optical absorption by interlayer excitons in transition metal dichalcogenide heterobilayers. Phys. Rev. B 97, 035306 (2018).
Rivera, P. et al. Valley-polarized exciton dynamics in a 2D semiconductor heterostructure. Science 351, 688–691 (2016).
Jin, C. et al. Imaging of pure spin-valley diffusion current in WS2-WSe2 heterostructures. Science 360, 893–896 (2018).
Nagler, P. et al. Giant magnetic splitting inducing near-unity valley polarization in van der Waals heterostructures. Nat. Commun. 8, 1551 (2017).
Jiang, C. et al. Microsecond dark-exciton valley polarization memory in two-dimensional heterostructures. Nat. Commun. 9, 753 (2018).
Hsu, W.-T. et al. Negative circular polarization emissions from WSe2/MoSe2 commensurate heterobilayers. Nat. Commun. 9, 1356 (2018).
Ciarrocchi, A. et al. Polarization switching and electrical control of interlayer excitons in two-dimensional van der Waals heterostructures. Nat. Photonics 13, 131-136 (2019).
Tran, K. et al. Moiré excitons in van der Waals heterostructures. Preprint at https://arxiv.org/abs/1807.03771 (2018).
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 6, 6242 (2015).
Nagler, P. et al. Interlayer exciton dynamics in a dichalcogenide monolayer heterostructure. 2D Mater. 4, 025112 (2017).
Miller, B. et al. Long-lived direct and indirect interlayer excitons in van der Waals heterostructures. Nano Lett. 17, 5229–5237 (2017).
Ross, J. S. et al. Interlayer exciton optoelectronics in a 2D heterostructure p–n junction. Nano Lett. 17, 638–643 (2017).
Zhang, C. et al. Interlayer couplings, moiré patterns, and 2D electronic superlattices in MoS2/WSe2 hetero-bilayers. Sci. Adv. 3, e1601459 (2017).
Bloch, I. Ultracold quantum gases in optical lattices. Nat. Phys. 1, 23–30 (2005).
Hong, X. et al. Ultrafast charge transfer in atomically thin MoS2/WS2 heterostructures. Nat. Nanotechnol. 9, 682–686 (2014).
He, Y.-M. et al. Single quantum emitters in monolayer semiconductors. Nat. Nanotechnol. 10, 497–502 (2015).
Srivastava, A. et al. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 10, 491–496 (2015).
Koperski, M. et al. Single photon emitters in exfoliated WSe2 structures. Nat. Nanotechnol. 10, 503–506 (2015).
Chakraborty, C., Kinnischtzke, L., Goodfellow, K. M., Beams, R. & Vamivakas, A. N. Voltage-controlled quantum light from an atomically thin semiconductor. Nat. Nanotechnol. 10, 507–511 (2015).
Tran, T. T., Bray, K., Ford, M. J., Toth, M. & Aharonovich, I. Quantum emission from hexagonal boron nitride monolayers. Nat. Nanotechnol. 11, 37–41 (2016).
Hanbicki, A. T. et al. Double indirect interlayer exciton in a MoSe2/WSe2 van der Waals heterostructure. ACS Nano 12, 4719–4726 (2018).
Kunstmann, J. et al. Momentum-space indirect interlayer excitons in transition-metal dichalcogenide van der Waals heterostructures. Nat. Phys. 14, 801–805 (2018).
Chakraborty, C. et al. 3D localized trions in monolayer WSe2 in a charge tunable van der Waals heterostructure. Nano Lett. 18, 2859–2863 (2018).
Yu, H., Liu, G.-B. & Yao, W. Brightened spin-triplet interlayer excitons and optical selection rules in van der Waals heterobilayers. 2D Mater. 5, 035021 (2018).
Wu, F., Lovorn, T. & MacDonald, A. H. Topological exciton bands in moiré heterojunctions. Phys. Rev. Lett. 118, 147401 (2017).
Schaibley, J. R. et al. Directional interlayer spin-valley transfer in two-dimensional heterostructures. Nat. Commun. 7, 13747 (2016).
Zhang, S. et al. Defect structure of localized excitons in a WSe2 monolayer. Phys. Rev. Lett. 119, 046101 (2017).
Palacios-Berraquero, C. et al. Large-scale quantum-emitter arrays in atomically thin semiconductors. Nat. Commun. 8, 15093 (2017).
Branny, A., Kumar, S., Proux, R. & Gerardot, B. D. Deterministic strain-induced arrays of quantum emitters in a two-dimensional semiconductor. Nat. Commun. 8, 15053 (2017).
Aivazian, G. et al. Magnetic control of valley pseudospin in monolayer WSe2. Nat. Phys. 11, 148–152 (2015).
Srivastava, A. et al. Valley Zeeman effect in elementary optical excitations of monolayer WSe2. Nat. Phys. 11, 141–147 (2015).
Li, Y. et al. Valley splitting and polarization by the Zeeman effect in monolayer MoSe2. Phys. Rev. Lett. 113, 266804 (2014).
MacNeill, D. et al. Breaking of valley degeneracy by magnetic field in monolayer MoSe2. Phys. Rev. Lett. 114, 037401 (2015).
Yao, W., Xiao, D. & Niu, Q. Valley-dependent optoelectronics from inversion symmetry breaking. Phys. Rev. B 77, 235406 (2008).
Wang, Y., Wang, Z., Yao, W., Liu, G.-B. & Yu, H. Interlayer coupling in commensurate and incommensurate bilayer structures of transition-metal dichalcogenides. Phys. Rev. B 95, 115429 (2017).
Acknowledgements
We acknowledge J. Fonseca for assistance with fabrication and E. Waks for photon intensity correlation measurements. This work was mainly supported by the Department of Energy (DoE), Basic Energy Sciences, Materials Sciences and Engineering Division (DE-SC0018171). The understanding of moiré physics was partially supported by DoE Pro-QM EFRC (DE-SC0019443). W.Y. and H.Y. were supported by the Croucher Foundation (Croucher Innovation Award) and the RGC of Hong Kong (HKU17302617). D.M. and J.Y. were supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. X.X. acknowledges support from the State of Washington funded Clean Energy Institute and from the Boeing Distinguished Professorship in Physics.
Reviewer information
Nature thanks David R. Reichman and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
X.X., W.Y., K.L.S. and P.R. conceived the experiment. P.R. fabricated the devices, assisted by K.L.S. and E.L.R. K.L.S. and P.R. performed the measurements, assisted by N.P.W. K.L.S., P.R., X.X., W.Y. and H.Y. analysed and interpreted the results. J.Y. and D.G.M. synthesized and characterized the bulk crystals. K.L.S., X.X., W.Y., P.R. and H.Y. wrote the paper with input from all authors. All authors discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Supplementary power-dependence data.
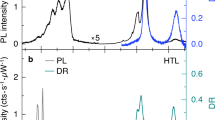
a, Interlayer exciton photoluminescence spectra at selected excitation powers for the θ = 2° sample of device 1. b, c, Photoluminescence spectra at low (blue) and high (red) power for the θ = 57° sample of device 2 (b) and the θ = 20° sample of device 1 (c). Insets show the Lorentzian fit to the representative photoluminescence peaks with the indicated linewidths. When the excitation reaches around 1 μW, a broad background characteristic of delocalized interlayer exciton emission begins to dominate the spectrum. This excitation intensity is consistent with the expected threshold required to fill the moiré lattice. In brief, for a twist angle of around 2°, the moiré wavelength is about 10 nm and the moiré supercell spans about 100 nm2. Considering the average interlayer exciton lifetime of around 100 ns (Extended Data Fig. 10) and assuming around 10% absorption, the approximate pump intensity required to fill the moiré superlattice with approximately 1 interlayer exciton per supercell is around 100 W cm−2 (around 1 μW for a beam size of 1 μm2). We note that, with the strong repulsive interaction of interlayer excitons, the moiré potential traps will also be broadened by the loading of more excitons in each trap.
Extended Data Fig. 2 Temperature-dependent photoluminescence.
a, b, Temperature dependence of the interlayer exciton photoluminescence spectrum for θ = 2° (a) and θ = 20° (b) samples of device 1. The excitation powers were 20 nW (a) and 1 μW (b). The trapped interlayer excitons vanish above about 30 K (around 2–3 meV). Future work is needed to determine the mechanisms that lead to this thermal energy scale.
Extended Data Fig. 3 Supplementary circular-polarization-resolved photoluminescence spectra.
Each panel represents data from a different sample with the indicated twist angle. The left and right graphs of each panel correspond to σ− and σ+ polarized excitation, and the red and blue curves indicate σ+ and σ− polarized photoluminescence components. Spectra from the θ = 2° and θ = 20° regions of device 1 are shown in a and c, whereas those from the θ = 6° and θ = 57° regions of device 2 are shown in b and e. The θ = 2° spectra in a were acquired from a different sample region than the spectra in Fig. 2c, and show a similarly strong polarization reversal. The spectra in d and f are from additional heterobilayers. The twist angle uncertainty is 1°.
Extended Data Fig. 4 Linear-polarization-resolved photoluminescence.
a–c, Photoluminescence intensity plots as a function of the linear polarization detection angle and photon energy under linearly polarized excitation for θ = 57° (a), 20° (b) and 2° (c). No linear photoluminescence polarization is observed.
Extended Data Fig. 5 Free and trapped interlayer exciton g-factor for θ ≈ 0°.
The data are acquired from the θ = 6° region of device 2 under linearly polarized excitation. a, Photoluminescence intensity plot of σ+ (right) and σ− (left) components as a function of applied magnetic field and photon energy. The broad background (free exciton) shifts with the same slope as the sharp trapped interlayer exciton on top. b, Valley Zeeman splitting (Δ) against applied magnetic field, from which a g-factor of 6.74 ± 0.05 is extracted from a linear fit (solid red line).
Extended Data Fig. 6 Uniformity of g-factors.
a–d, Photoluminescence intensity plots of 2° (a), 3° (b), 56° (c) and 60° (d) heterobilayers as a function of applied magnetic field and photon energy. The data for the 2° heterobilayer (a) were acquired from a different spot than the data in Fig. 3c. The excitation is linearly polarized. Top, circularly polarized photoluminescence spectra at 3 T. Middle, photoluminescence intensity as a function of applied magnetic field, displaying a clear linear Zeeman shift of the σ+ and σ− components. Bottom, valley Zeeman splitting (Δ) against applied magnetic field. Linear fits (solid red lines) give effective g-factors of heterobilayers at different twist angles, yielding 6.73 ± 0.02, 6.72 ± 0.03, −15.88 ± 0.09 and −15.91 ± 0.02 for a–d, respectively. The data confirm the g-factor uniformity across the same sample as well as across different samples with similar twist angles.
Extended Data Fig. 7 Calibrated photoluminescence spectra for a comparison of the photoluminescence intensity from heterobilayers with different twist angles.
a–c, Photoluminescence spectra of samples in which θ = 57° (a), 20° (b) and 2° (c). The photoluminescence intensity of samples in which θ = 2° and θ = 57° is about 100 times higher than that of θ = 20°. Excitation powers were 10 nW for a and c and 100 nW for b. The photoluminescence intensity for the heterobilayer in which θ = 20° is still in the linear regime for powers less than 100 nW. Aside from the excitation power, the data from all three twist angles were acquired under identical experimental conditions to facilitate their comparison.
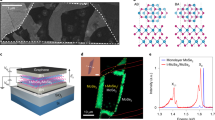
Extended Data Fig. 8 Heterobilayer moiré pattern for twist angles close to 21.8°.
a–c, Three high-symmetry stacking patterns exist for the heterobilayer with a commensurate 21.8° twist angle, in which the two layers have the same lattice constant a. The dashed diamonds indicate the smallest supercells, the periodicity of which is \(\sqrt{7}a\). The large (small) solid green dots denote the metal, M (chalcogen, X) sites in the electron layer, whereas the large (small) empty orange dots denote the metal, M (chalcogen, X) sites in the hole layer. a, The stacking in which two M sites in different layers horizontally overlap. b, The stacking in which two hexagon centres (h sites) in different layers horizontally overlap. c, The stacking in which two X sites in different layers horizontally overlap. Because M, X and h are the C3 rotation centres of the monolayers, the stacking configurations in a, b and c are all C3 symmetric. d, Illustration of the moiré pattern when the twist angle slightly deviates from 21.8° (θ = 20° here). Red circles marked by A, B and C are the local regions that are nearly indistinguishable from the commensurate 21.8° pattern in a, b and c, respectively. The black diamonds are the \(\sqrt{7}a\times \sqrt{7}a\) supercells of the local regions.
Extended Data Fig. 9 Spatial homogeneity of interlayer exciton photoluminescence.
The centre image shows a spatial map of the integrated photoluminescence for the θ = 2° heterobilayer, and the plots along the outside show selected interlayer exciton photoluminescence spectra at different sample locations. The photoluminescence is bright across a wide region of the sample, except along one edge of a crack that runs through the sample (note the correspondence to the sample height map in Fig. 1c). Narrow-line photoluminescence emission is a general feature of the photoluminescence spectra across the sample, as seen in the selected spectra from spatially distinct regions of the sample. The number of narrow-line peaks, their intensities and their energy distribution is inhomogeneous across the sample. The origin of this inhomogeneity is an important topic for further study.
Extended Data Fig. 10 Time- and polarization-resolved photoluminescence of trapped interlayer excitons.
a, Time-resolved photoluminescence intensity traces for σ+ (red) and σ− (blue) emission from a single line of the θ = 57° heterobilayer under σ+ excitation. Inset, photoluminescence spectra of the emission line. Vertical dashed lines indicate the spectral collection bandwidth. b, Time-resolved valley polarization, η, under σ+ (orange, top) and σ− (green, bottom) excitation.
Rights and permissions
About this article
Cite this article
Seyler, K.L., Rivera, P., Yu, H. et al. Signatures of moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers. Nature 567, 66–70 (2019). https://doi.org/10.1038/s41586-019-0957-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-0957-1
This article is cited by
-
Topological minibands and interaction driven quantum anomalous Hall state in topological insulator based moiré heterostructures
Nature Communications (2024)
-
Room-temperature quantum emission from interface excitons in mixed-dimensional heterostructures
Nature Communications (2024)
-
Dynamically tunable moiré exciton Rydberg states in a monolayer semiconductor on twisted bilayer graphene
Nature Materials (2024)
-
Energy transfer driven brightening of MoS2 by ultrafast polariton relaxation in microcavity MoS2/hBN/WS2 heterostructures
Nature Communications (2024)
-
Van der Waals epitaxy of tunable moirés enabled by alloying
Nature Materials (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.