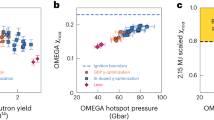
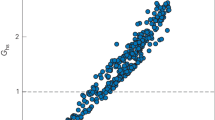
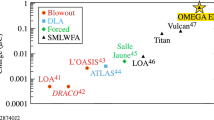
Abstract
Focusing laser light onto a very small target can produce the conditions for laboratory-scale nuclear fusion of hydrogen isotopes. The lack of accurate predictive models, which are essential for the design of high-performance laser-fusion experiments, is a major obstacle to achieving thermonuclear ignition. Here we report a statistical approach that was used to design and quantitatively predict the results of implosions of solid deuterium–tritium targets carried out with the 30-kilojoule OMEGA laser system, leading to tripling of the fusion yield to its highest value so far for direct-drive laser fusion. When scaled to the laser energies of the National Ignition Facility (1.9 megajoules), these targets are predicted to produce a fusion energy output of about 500 kilojoules—several times larger than the fusion yields currently achieved at that facility. This approach could guide the exploration of the vast parameter space of thermonuclear ignition conditions and enhance our understanding of laser-fusion physics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
Raw data were generated at the LLE’s OMEGA Laser Facility. Derived data supporting the findings of this study are available from the corresponding author upon reasonable request.
References
Nuckolls, J., Wood, L., Thiessen, A. & Zimmerman, G. Laser compression of matter to super-high densities: thermonuclear (CTR) applications. Nature 239, 139–142 (1972).
Atzeni, S. & Meyer-ter-Vehn, J. The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter 1st edn (Oxford Univ. Press, Oxford, 2004).
Slutz, S. A. et al. Pulsed-power-driven cylindrical liner implosions of laser preheated fuel magnetized with an axial field. Phys. Plasmas 17, 056303 (2010).
Craxton, R. S. et al. Direct-drive inertial confinement fusion: a review. Phys. Plasmas 22, 110501 (2015).
Lindl, J. D. Inertial Confinement Fusion: The Quest for Ignition and Energy Gain Using Indirect Drive (Springer-Verlag, New York, 1998).
Giorgini, S., Pitaevskii, L. P. & Stringari, S. Theory of ultracold atomic Fermi gases. Rev. Mod. Phys. 80, 1215–1274 (2008).
Christopherson, A. R. et al. A comprehensive alpha-heating model for inertial confinement fusion. Phys. Plasmas 25, 012703 (2018).
Betti, R. et al. Alpha heating and burning plasmas in inertial confinement fusion. Phys. Rev. Lett. 114, 255003 (2015).
Hurricane, O. A. et al. Inertially confined fusion plasmas dominated by alpha-particle self-heating. Nat. Phys. 12, 800–806 (2016).
Betti, R. et al. Thermonuclear ignition in inertial confinement fusion and comparison with magnetic confinement. Phys. Plasmas 17, 058102 (2010).
Chang, P. Y. et al. Generalized measurable ignition criterion for inertial confinement fusion. Phys. Rev. Lett. 104, 135002 (2010).
Spears, B. K. et al. Performance metrics for inertial confinement fusion implosions: aspects of the technical framework for measuring progress in the National Ignition Campaign. Phys. Plasmas 19, 056316 (2012).
Betti, R. & Hurricane, O. A. Inertial-confinement fusion with lasers. Nat. Phys. 12, 435–448 (2016); corrigendum 12, 717 (2016).
Le Pape, S. et al. Fusion energy output greater than the kinetic energy of an imploding shell at the National Ignition Facility. Phys. Rev. Lett. 120, 245003 (2018).
Hurricane, O. A. et al. Fuel gain exceeding unity in an inertially confined fusion implosion. Nature 506, 343–348 (2014); corrigendum 510, 432 (2014).
Campbell, E. M. & Hogan, W. J. The National Ignition Facility – applications for inertial fusion energy and high-energy-density science. Plasma Phys. Contr. Fusion 41, B39–B56 (1999).
Edwards, M. J. et al. Progress towards ignition on the National Ignition Facility. Phys. Plasmas 20, 070501 (2013).
Lindl, J. et al. Review of the National Ignition Campaign 2009–2012 Phys. Plasmas 21, 020501 (2014); erratum 21, 129902 (2014).
Goncharov, V. N. et al. National direct-drive program on OMEGA and the National Ignition Facility. Plasma Phys. Contr. Fusion 59, 014008 (2017).
Marinak, M. M. et al. Three-dimensional HYDRA simulations of National Ignition Facility targets. Phys. Plasmas 8, 2275–2280 (2001).
Zimmerman, G., Kershaw, D., Bailey, D. & Harte, J. The LASNEX code for inertial confinement fusion. J. Opt. Soc. Am. 68, 549 (1978).
Radha, P. B. et al. Two-dimensional simulations of plastic-shell, direct-drive implosions on OMEGA. Phys. Plasmas 12, 032702 (2005).
Delettrez, J., Epstein, R., Richardson, M. C., Jaanimagi, P. A. & Henke, B. L. Effect of laser illumination nonuniformity on the analysis of time-resolved X-ray measurements in UV spherical transport experiments. Phys. Rev. A 36, 3926–3934 (1987).
Atzeni, S. et al. Fluid and kinetic simulation of inertial confinement fusion plasmas. Comput. Phys. Commun. 169, 153–159 (2005).
Clark, D. S. et al. Radiation hydrodynamics modeling of the highest compression inertial confinement fusion ignition experiment from the National Ignition Campaign. Phys. Plasmas 22, 022703 (2015).
Igumenshchev, I. V. et al. Three-dimensional modeling of direct-drive cryogenic implosions on OMEGA. Phys. Plasmas 23, 052702 (2016).
Igumenshchev, I. V. et al. Crossed-beam energy transfer in implosion experiments OMEGA. Phys. Plasmas 17, 122708 (2010).
Michel, D. T. et al. Measurements of the ablation-front trajectory and low-mode nonuniformity in direct-drive implosions using X-ray self-emission shadowgraphy. High Power Laser Sci. Eng. 3, e19 (2015).
Goncharov, V. N. et al. Early stage of implosion in inertial confinement fusion: shock timing and perturbation evolution. Phys. Plasmas 13, 012702 (2006).
Hu, S. X. et al. First-principles equation of state of polystyrene and its effect on inertial confinement fusion implosions. Phys. Rev. E 92, 043104 (2015).
Boehly, T. R. et al. Initial performance results of the OMEGA Laser System. Opt. Commun. 133, 495–506 (1997).
Regan, S. P. et al. Demonstration of fuel hot-spot pressure in excess of 50 Gbar for direct-drive, layered deuterium–tritium implosions on OMEGA. Phys. Rev. Lett. 117, 025001 (2016).
Bose, A. et al. Core conditions for alpha heating attained in direct-drive inertial confinement fusion. Phys. Rev. E 94, 011201 (2016).
Robey, H. F. et al. Measurement of high-pressure shock waves in cryogenic deuterium-tritium ice layered capsule implosions on NIF. Phys. Rev. Lett. 111, 065003 (2013).
Betti, R. et al. Shock ignition of thermonuclear fuel with high areal density. Phys. Rev. Lett. 98, 155001 (2007).
Kilkenny, J. D. et al. A review of the ablative stabilization of the Rayleigh–Taylor instability in regimes relevant to inertial confinement fusion. Phys. Plasmas 1, 1379–1389 (1994).
Brouillette, M. The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34, 445–468 (2002).
Peterson, J. L. et al. Enhancing hohlraum design with artificial neural networks. Bull. Am. Phys. Soc. 62 http://meetings.aps.org/link/BAPS.2017.DPP.BO7.6 (2017).
Salvatier, J., Wiecki, T. V. & Fonnesbeck, C. Probabilistic programming in python using PyMC3. PeerJ Comput. Sci. 2, e55 (2016).
Boehly, T. R. et al. Optical and plasma smoothing of laser imprinting in targets driven by lasers with SSD bandwidths up to 1 THz. Phys. Plasmas 8, 2331–2337 (2001).
Hu, S. X. et al. Understanding the effects of laser imprint on plastic-target implosions on OMEGA. Phys. Plasmas 23, 102701 (2016).
Murphy, T. J., Chrien, R. E. & Klare, K. A. Interpretation of neutron time-of-flight signals from current-mode detectors. Rev. Sci. Instrum. 68, 610–613 (1997).
Murphy, T. J. The effect of turbulent kinetic energy on inferred ion temperature from neutron spectra. Phys. Plasmas 21, 072701 (2014).
Woo, K. M. et al. Effects of residual kinetic energy on yield degradation and ion temperature asymmetries in inertial confinement fusion implosions. Phys. Plasmas 25, 052704 (2018).
Nora, R. et al. Theory of hydro-equivalent ignition for inertial fusion and its applications to OMEGA and the National Ignition Facility. Phys. Plasmas 21, 056316 (2014).
Bose, A. et al. Analysis of trends in implosion observables for direct-drive cryogenic implosions on OMEGA. Phys. Plasmas 25, 062701 (2018).
Smalyuk, V. A. et al. Role of hot-electron preheating in the compression of direct-drive imploding targets with cryogenic D2 ablators. Phys. Rev. Lett. 100, 185005 (2008).
Forrest, C. J. et al. High-resolution spectroscopy used to measure inertial confinement fusion neutron spectra on OMEGA. Rev. Sci. Instrum. 83, 10D919 (2012).
Casey, D. T. et al. The magnetic recoil spectrometer for measurements of the absolute neutron spectrum at OMEGA and the NIF. Rev. Sci. Instrum. 84, 043506 (2013).
Donaldson, W. R., Boni, R., Keck, R. L. & Jaanimagi, P. A. A self-calibrating, multichannel streak camera for inertial confinement fusion applications. Rev. Sci. Instrum. 73, 2606–2615 (2002).
Edgell, D. H. et al. Three-dimensional characterization of cryogenic target ice layers using multiple shadowgraph views. Fus. Sci. Technol. 49, 616–625 (2006).
Hu, S. X., Militzer, B., Goncharov, V. N. & Skupsky, S. First-principles equation-of-state table of deuterium for inertial confinement fusion applications. Phys. Rev. B. 84, 224109 (2011).
Zhou, C. D. & Betti, R. A measurable Lawson criterion and hydro-equivalent curves for inertial confinement fusion. Phys. Plasmas 15, 102707 (2008); correction 16, 079905 (2009).
Hoffman, M. D. & Gelman, A. The no-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15, 1593–1623 (2014).
Goncharov, V. N. et al. Improving the hot-spot pressure and demonstrating ignition hydrodynamic equivalence in cryogenic deuterium–tritium implosions on OMEGA. Phys. Plasmas 21, 056315 (2014).
Marozas, J. A. et al. First observation of cross-beam energy transfer mitigation for direct-drive inertial confinement fusion implosions using wavelength detuning at the National Ignition Facility. Phys. Rev. Lett. 120, 085001 (2018).
Rosenberg, M. J. et al. Origins and scaling of hot-electron preheat in ignition-scale direct-drive inertial confinement fusion experiments. Phys. Rev. Lett. 120, 055001 (2018).
Zhou, C. D. & Betti, R. Hydrodynamic relations for direct-drive fast-ignition and conventional inertial confinement fusion implosions. Phys. Plasmas 14, 072703 (2007).
Acknowledgements
This material is based on work supported by the Department of Energy National Nuclear Security Administration under award numbers DE-NA0003856 and DENA0001944, the Department of Energy Office of Fusion Energy Sciences under award number DE-FC02-04ER54789, the University of Rochester and the New York State Energy Research and Development Authority. This report was prepared as an account of work sponsored by an agency of the US Government. Neither the US Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness or usefulness of any information, apparatus, product or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process or service by trade name, trademark, manufacturer or otherwise does not necessarily constitute or imply its endorsement, recommendation or favouring by the US Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the US Government or any agency thereof.
Reviewer information
Nature thanks I. Kaganovich, R. Scott and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
All authors contributed to the work presented in this paper. A.A.S., A.M. and J. Palastro were responsible for theoretical and experimental work on hot-electron pre-heating, and J. Peebles investigated high-ℓ-mode instabilities due to laser imprinting, both of which were used in constraining the optimization process of this work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Posterior predictive distributions for the parameters in equation (6).
The intercept parameter refers to the constant Cj in equation (5), ε refers to the noise parameter in equation (8) and the remaining parameters are the μi values for the corresponding simulated quantities, as in equation (5). The Markov chains for each parameter are converged over 5,000 steps. The tails of the distributions have the same sign as the mean and are not excessively wide when compared to the mean. All these indicate that the model is well specified.
Extended Data Fig. 2 Posterior predictive distributions for the parameters in equation (7).
The intercept parameter refers to the constant Cj in equation (5), ε refers to the noise parameter in equation (8) and the remaining parameters are the μi values for the corresponding simulated quantities, as in equation (5). As in Extended Data Fig. 1, these results indicate that the model is well specified; we note that this does not guarantee that the model will have any predictive power.
Extended Data Fig. 3 The effect of RT on the yield is less than 10% for the vast majority of implosions.
Vertical error bars are one standard deviation of \({R}_{T}^{-0.6}\). Because the yield is proportional to \({R}_{T}^{-0.6}\) in equation (7), and the vast majority of implosions carried out at OMEGA are repeatable, the empirical correction factor in equation (7) varies by less than 10% for most OMEGA implosions. This justifies the use of this parameter to account for the occasional shot with large random nonuniformities.
Extended Data Fig. 4 Areal densities for high-convergence implosions are well predicted.
The dashed line is the y = x line on which the data points would lie if the experimental areal density were perfectly modelled by the power-law dependence. As the convergence increases, the safety margin for a nominal implosion becomes thinner and makes designing these implosions more challenging. A predictive model for the areal density was built using the framework presented in this paper (training data are shown by blue circles). The areal density was increased from that of shot 87266 (green circle) over four shot days (orange circles) until the highest values were reached in July 2018. The yields for these implosions are marked.
Extended Data Fig. 5 Comparison of prediction accuracies of the statistical model and 1D simulations.
a, b, Predictions for the areal density (a) and neutron yield (b) including the second phase of the Optimization Campaign. The predictions from the statistical model (blue) remain accurate for implosions from both phases of the Optimization Campaign, whereas the corresponding simulated 1D quantities from LILAC (red) remain inaccurate and overpredict potential increases in performance. Horizontal error bars and centre values represent one standard deviation and mean, respectively, for 500 draws from the posterior distribution of the statistical model. Vertical error bars represent one standard deviation for the neutron yield and areal density detectors. The dashed line is the y = x line on which the data points would lie if the prediction perfectly matched the measurement.
Extended Data Fig. 6 Power-law dependence of the simulated yield on simulated parameters for initial conditions used in the Optimization Campaign.
The dashed line is the y = x line on which the data points would lie if the simulated yield were perfectly modelled by the power-law dependence. The simulated yield (Ysim) is well represented by power-law relations to the simulated implosion velocity (\({V}_{{\rm{i}}{\rm{m}}{\rm{p}}}^{{\rm{s}}{\rm{i}}{\rm{m}}}\)), mass (\({M}_{{\rm{s}}{\rm{t}}{\rm{a}}{\rm{g}}}^{{\rm{s}}{\rm{i}}{\rm{m}}}\)) and areal density (ρRsim). Although the exponents are not identical to those from analytical theory, physical intuition has provided a good basis for variable selection.
Rights and permissions
About this article
Cite this article
Gopalaswamy, V., Betti, R., Knauer, J.P. et al. Tripled yield in direct-drive laser fusion through statistical modelling. Nature 565, 581–586 (2019). https://doi.org/10.1038/s41586-019-0877-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-019-0877-0
This article is cited by
-
A boost for laser fusion
Nature Physics (2024)
-
A Machine Learning Method for the Optimization Design of Laser Pulse in Fast Ignition Simulations
Journal of Fusion Energy (2024)
-
Demonstration of a hydrodynamically equivalent burning plasma in direct-drive inertial confinement fusion
Nature Physics (2024)
-
Demonstration of hot-spot fuel gain exceeding unity in direct-drive inertial confinement fusion implosions
Nature Physics (2024)
-
Development of an ultrafast detector and demonstration of its oscillographic application
Nuclear Science and Techniques (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.