Abstract
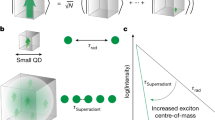
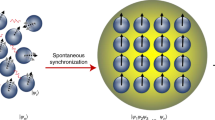
An ensemble of emitters can behave very differently from its individual constituents when they interact coherently via a common light field. After excitation of such an ensemble, collective coupling can give rise to a many-body quantum phenomenon that results in short, intense bursts of light—so-called superfluorescence1. Because this phenomenon requires a fine balance of interactions between the emitters and their decoupling from the environment, together with close identity of the individual emitters, superfluorescence has thus far been observed only in a limited number of systems, such as certain atomic and molecular gases and a few solid-state systems2,3,4,5,6,7. The generation of superfluorescent light in colloidal nanocrystals (which are bright photonic sources practically suited for optoelectronics8,9) has been precluded by inhomogeneous emission broadening, low oscillator strength, and fast exciton dephasing. Here we show that caesium lead halide (CsPbX3, X = Cl, Br) perovskite nanocrystals10,11,12,13 that are self-organized into highly ordered three-dimensional superlattices exhibit key signatures of superfluorescence. These are dynamically red-shifted emission with more than 20-fold accelerated radiative decay, extension of the first-order coherence time by more than a factor of four, photon bunching, and delayed emission pulses with Burnham–Chiao ringing behaviour14 at high excitation density. These mesoscopically extended coherent states could be used to boost the performance of opto-electronic devices15 and enable entangled multi-photon quantum light sources16,17.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Bonifacio, R. & Lugiato, L. A. Cooperative radiation processes in two-level systems: superfluorescence. Phys. Rev. A 11, 1507–1521 (1975).
Skribanowitz, N., Herman, I. P., MacGillivray, J. C. & Feld, M. S. Observation of Dicke superradiance in optically pumped HF gas. Phys. Rev. Lett. 30, 309–312 (1973).
Malcuit, M. S., Maki, J. J., Simkin, D. J. & Boyd, R. W. Transition from superfluorescence to amplified spontaneous emission. Phys. Rev. Lett. 59, 1189–1192 (1987).
Miyajima, K., Kagotani, Y., Saito, S., Ashida, M. & Itoh, T. Superfluorescent pulsed emission from biexcitons in an ensemble of semiconductor quantum dots. J. Phys. Condens. Matter 21, 195802 (2009).
Dai, D. C. & Monkman, A. P. Observation of superfluorescence from a quantum ensemble of coherent excitons in a ZnTe crystal: evidence for spontaneous Bose-Einstein condensation of excitons. Phys. Rev. B 84, 115206 (2011).
Noe, G. T. II et al. Giant superfluorescent bursts from a semiconductor magneto-plasma. Nat. Phys. 8, 219–224 (2012).
Cong, K. et al. Dicke superradiance in solids. J. Opt. Soc. Am. B 33, C80–C101 (2016).
Talapin, D. V., Lee, J.-S., Kovalenko, M. V. & Shevchenko, E. V. Prospects of colloidal nanocrystals for electronic and optoelectronic applications. Chem. Rev. 110, 389–458 (2010).
Kovalenko, M. V. et al. Prospects of nanoscience with nanocrystals. ACS Nano 9, 1012–1057 (2015).
Protesescu, L. et al. Nanocrystals of cesium lead halide perovskites (CsPbX3, X=Cl, Br, and I): novel optoelectronic materials showing bright emission with wide color gamut. Nano Lett. 15, 3692–3696 (2015).
Rainò, G. et al. Single cesium lead halide perovskite nanocrystals at low temperature: fast single-photon emission, reduced blinking, and exciton fine structure. ACS Nano 10, 2485–2490 (2016).
Fu, M. et al. Neutral and charged exciton fine structure in single lead halide perovskite nanocrystals revealed by magneto-optical spectroscopy. Nano Lett. 17, 2895–2901 (2017).
Kovalenko, M. V., Protesescu, L. & Bodnarchuk, M. I. Properties and potential optoelectronic applications of lead halide perovskite nanocrystals. Science 358, 745–750 (2017).
Burnham, D. C. & Chiao, R. Y. Coherent resonance fluorescence excited by short light pulses. Phys. Rev. 188, 667–675 (1969).
Kagan, C. R. & Murray, C. B. Charge transport in strongly coupled quantum dot solids. Nat. Nanotechnol. 10, 1013–1026 (2015).
Afek, I., Ambar, O. & Silberberg, Y. High-NOON states by mixing quantum and classical light. Science 328, 879–881 (2010).
Muñoz, C. S. et al. Emitters of N-photon bundles. Nat. Photon. 8, 550–555 (2014).
Dicke, R. H. Coherence in spontaneous radiation processes. Phys. Rev. 93, 99–110 (1954).
Spano, F. C. The spectral signatures of Frenkel polarons in H- and J-aggregates. Acc. Chem. Res. 43, 429–439 (2010).
Bradac, C. et al. Room-temperature spontaneous superradiance from single diamond nanocrystals. Nat. Commun. 8, 1205 (2017).
Scheibner, M. et al. Superradiance of quantum dots. Nat. Phys. 3, 106–110 (2007).
Heinzen, D. J., Thomas, J. E. & Feld, M. S. Coherent ringing in superfluorescence. Phys. Rev. Lett. 54, 677–680 (1985).
Shirasaki, Y., Supran, G. J., Bawendi, M. G. & Bulović, V. Emergence of colloidal quantum-dot light-emitting technologies. Nat. Photon. 7, 13–23 (2013).
Becker, M. A. et al. Bright triplet excitons in caesium lead halide perovskites. Nature 553, 189–193 (2018).
Boles, M. A., Engel, M. & Talapin, D. V. Self-assembly of colloidal nanocrystals: from intricate structures to functional materials. Chem. Rev. 116, 11220–11289 (2016).
Murray, C. B., Kagan, C. R. & Bawendi, M. G. Synthesis and characterization of monodisperse nanocrystals and close-packed nanocrystal assemblies. Annu. Rev. Mater. Sci. 30, 545–610 (2000).
Geuchies, J. J. et al. In situ study of the formation mechanism of two-dimensional superlattices from PbSe nanocrystals. Nat. Mater. 15, 1248–1254 (2016).
Nagaoka, Y. et al. Nanocube superlattices of cesium lead bromide perovskites and pressure-induced phase transformations at atomic and mesoscale levels. Adv. Mater. 29, 1606666 (2017).
Temnov, V. V. & Woggon, U. Superradiance and subradiance in an inhomogeneously broadened ensemble of two-level systems coupled to a low-Q cavity. Phys. Rev. Lett. 95, 243602 (2005).
Whittaker, D. M. & Eastham, P. R. Coherence properties of the microcavity polariton condensate. Europhys. Lett. 87, 27002 (2009).
Jahnke, F. et al. Giant photon bunching, superradiant pulse emission and excitation trapping in quantum-dot nanolasers. Nat. Commun. 7, 11540 (2016).
Temnov, V. V. & Woggon, U. Photon statistics in the cooperative spontaneous emission. Opt. Express 17, 5774 (2009).
Ishikawa, A., Miyajima, K., Ashida, M., Itoh, T. & Ishihara, H. Theory of superfluorescence in highly inhomogeneous quantum systems. J. Phys. Soc. Jpn. 85, 034703 (2016).
DeVoe, R. G. & Brewer, R. G. Observation of superradiant and subradiant spontaneous emission of two trapped ions. Phys. Rev. Lett. 76, 2049–2052 (1996).
Bienaimé, T., Piovella, N. & Kaiser, R. Controlled Dicke subradiance from a large cloud of two-level systems. Phys. Rev. Lett. 108, 123602 (2012).
Guerin, W., Rouabah, M. T. & Kaiser, R. Light interacting with atomic ensembles: collective, cooperative and mesoscopic effects. J. Mod. Opt. 64, 895–907 (2017).
van Driel, A. F. et al. Statistical analysis of time-resolved emission from ensembles of semiconductor quantum dots: interpretation of exponential decay models. Phys. Rev. B 75, 035329 (2007).
Naeem, A. et al. Giant exciton oscillator strength and radiatively limited dephasing in two-dimensional platelets. Phys. Rev. B 91, 121302 (2015).
Acknowledgements
We thank D. J. Norris, C. Schwemmer, D. Urbonas and F. Scafirimuto for helpful discussions. F. Krieg is acknowledged for providing additional samples for control experiments. M.A.B., M.V.K., T.S., R.F.M. and G.R. acknowledge support from the European Union’s Horizon-2020 programme through the Marie-Sklodowska Curie ITN network PHONSI (H2020-MSCA-ITN-642656) and the Swiss State Secretariat for Education Research and Innovation (SERI). M.I.B. acknowledges financial support from the Swiss National Science Foundation (SNF Ambizione grant no. PZENP2_154287). M.V.K. acknowledges financial support from the European Research Council under the European Union’s Seventh Framework Program (FP/2007-2013)/ERC Grant Agreement no. 306733 (NANOSOLID Starting Grant).
Reviewer information
Nature thanks C. Kagan and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
The work originated from continuing interactions between G.R., M.V.K., R.F.M. and T.S. M.I.B. prepared the samples and performed their structural characterization. G.R., M.A.B. and T.S. performed the optical experiments, and interpreted the data with input from R.F.M. G.R. and M.A.B. wrote the manuscript with input from all the co-authors. R.F.M., M.V.K. and T.S. supervised the work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Quantitative analysis of CsPbBr3 NC size distribution.
a, Low-resolution TEM image of the NC material used to prepare the superlattices. b, Histogram of NC sizes (of >100 NCs) as obtained from TEM image analysis. The solid line is a fit with a normal distribution, and the given mean size (9.45 nm) and standard deviation (0.41 nm) are obtained from this fit.
Extended Data Fig. 2 HAADF-STEM image of a single superlattice of CsPbBr3 NCs.
Individual NCs (bright spots in the image) are well-resolved.
Extended Data Fig. 3 PL excitation measurement of CsPbBr3 QD superlattices.
Using a weak, tunable excitation source, we plot the PL intensity (black circles) obtained at 2.30 eV photon energy as a function of excitation photon energy. The shaded areas are Gaussian peak fits. This PL excitation measurement shows that the coupled QD feature (red) is also present in absorption, in addition to the peak from uncoupled QDs (blue) and energetically higher states.
Extended Data Fig. 4 Power-dependent PL properties of CsPbBr3 QD superlattices.
a, Colour-coded PL emission in the low-power excitation regime, shown for increasing excitation fluence (in nJ cm−2) of 10 (light green), 60 (light blue), 150 (yellow) 310 (dark green) and 600 (dark blue). b, PL intensity integrated over the spectral emission range of the uncoupled QDs (‘QD intensity’, blue circles) and coupled QDs (‘SF intensity’, dark-red circles) in a log–log plot and the total emitted intensity (yellow circles). Fits to the data reveal linear behaviour, as represented by fitted power-law exponents m of approximately 1. c, Colour-coded PL emission in the high-power excitation regime, shown for increasing excitation fluence (in μJ cm−2) of 330 (light green), 1,270 (light blue), 2,130 (yellow), 3,470 (dark green) and 6,330 (dark blue). d, As b, but for the high-power excitation regime. Fits to the data reveal a power-law behaviour with a linear increase for the SF emission, a slightly sublinear increase for the uncoupled QDs and a less sublinear increase for the total emitted intensity.
Extended Data Fig. 5 Gaussian first-order coherence decay and photon bunching in pulsed excitation of CsPbBr3 QD superlattices.
a, First-order coherence of the coupled QD emission extracted from the fringe visibility of the interferograms as a function of delay time between the arms of a Michelson interferometer, revealing a mixture of Gaussian (Kubo) and exponential decay (for some of the superlattices). The red solid line is a fit with a mixed Gaussian/exponential model function. b, Second-order photon correlation measurement of the coupled QD emission from a single superlattice showing photon bunching at zero delay under pulsed excitation with a 40 MHz repetition rate.
Extended Data Fig. 6 SF in CsPbBr2Cl QD superlattices.
a, Band-pass filtered PL spectra of uncoupled QD emission (blue) and coupled QD emission (red) from CsPbBr2Cl perovskite superlattices. b, Second-order photon correlation measurements of uncoupled QD emission (top panel, g(2)(τ) = 1), showing a flat correlation function, and of coupled QD emission (lower panel, g(2)(0) = 1.15), showing photon bunching.
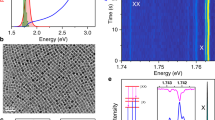
Extended Data Fig. 7 SF decay and dynamic red-shift of CsPbBr3 QD superlattices.
a, PL spectra (integrated over a 2 ps time window) at different time delays on a semi-log scale. b, The PL spectra are fitted to a single Gaussian peak function, and the fitted peak amplitude as a function of the emission energy is plotted for various excitation densities (see key). Green arrows indicate the time evolution of the emission peak. The black dashed line denotes the mean energy at the lowest excitation density, and the grey shaded area is the peak’s FWHM. c, Fitted peak centre energy as a function of time for various excitation densities (see key). d, Fast and slow PL decay time components τ1 and τ2 of the SF bi-exponential fit model as a function of excitation density on a semi-log plot. The error bars represent the parameters’ fit uncertainty.
Extended Data Fig. 8 Burnham–Chiao ringing behaviour in CsPbBr2Cl QD superlattices.
a, Streak camera image of SF dynamics obtained with a high excitation density of 1,600 μJ cm−2. b, Extracted time-resolved emission intensity traces for three different excitation powers (see key). Solid lines are best-fits to a model that employs a bi-exponential decay function with damped oscillations. c, Top, effective SF decay time (blue circles) as a function of the excitation fluence fitted according to the SF model (solid blue line). Middle, dark-red circles represent the peak SF emission intensity that increases superlinearly with excitation power, corresponding to a power-law dependence with an exponent α = 1.3 ± 0.1 (solid dark-red line). Bottom, the extracted delay time τD (green circles) decreases at high excitation power due to the increased interaction among the emitters. The green solid line is the best fit according the model described in the Methods section. The error bars represent the parameters’ fit uncertainty.
Extended Data Fig. 9 SF decay and dynamic red-shift of CsPbBr2Cl QD superlattices.
a, PL spectra (integrated over a 2 ps time window) at different time delays on a semi-log scale. b, The PL spectra are fitted to a single Gaussian peak function, and the fitted peak amplitude as a function of the emission energy is plotted for various excitation densities (see key). Green arrows indicate the time evolution of the emission peak. The black dashed line denotes the mean energy at the lowest excitation density, and the grey shaded area is the peak’s FWHM. c, Fitted peak centre energy as a function of time for various excitation densities (see key). d, Fast and slow PL decay time components τ1 and τ2 of the SF bi-exponential fit model as a function of excitation density. The error bars represent the parameters’ fit uncertainty.
Extended Data Fig. 10 PL decay from a control sample of diluted CsPbBr3 QDs.
a, Streak camera measurement of a control sample prepared by spin-coating a low concentration of CsPbBr3 QDs dispersed in polystyrene such that no QD coupling is realized. The excitation conditions were comparable to those used in Fig. 5 (an excitation density of 1,600 µJ cm−2 was used here). However, the relatively long decay time requires that a longer time range with a lower temporal resolution compared to the measurement in Fig. 5 has to be used on the streak camera. The absence of dynamic red-shift, accelerated decay and ringing proves that the observed SF features cannot be explained by single QD physics but are due to a multi-particle effect. b, Time-resolved PL trace (blue) obtained from these streak data. For direct comparison, the equivalent data from a superlattice sample exhibiting SF (Fig. 5b, 1,200 µJ cm−2) is shown (dark red). Inset, instrument response function of the streak camera. Using the same instrument settings as for the measurement on superlattices, the temporal response of the streak camera using scattered light from a 100-fs laser pulse at 400 nm gives a Gaussian-shaped instrument response with a FWHM of 4.3 ps (black circles); a Gaussian fit is shown as the red solid line.
Rights and permissions
About this article
Cite this article
Rainò, G., Becker, M.A., Bodnarchuk, M.I. et al. Superfluorescence from lead halide perovskite quantum dot superlattices. Nature 563, 671–675 (2018). https://doi.org/10.1038/s41586-018-0683-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0683-0
Keywords
This article is cited by
-
Observation of transition from superfluorescence to polariton condensation in CsPbBr3 quantum dots film
Light: Science & Applications (2024)
-
Coherent electronic coupling in quantum dot solids induces cooperative enhancement of nonlinear optoelectronic responses
Nature Nanotechnology (2024)
-
Single-photon superradiance in individual caesium lead halide quantum dots
Nature (2024)
-
Full characterization of superradiant pulses generated from a free-electron laser oscillator
Scientific Reports (2023)
-
Universal scaling laws for charge-carrier interactions with quantum confinement in lead-halide perovskites
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.