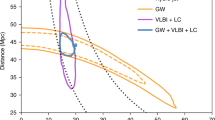
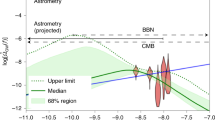
Abstract
Gravitational-wave detections provide a novel way to determine the Hubble constant1,2,3, which is the current rate of expansion of the Universe. This ‘standard siren’ method, with the absolute distance calibration provided by the general theory of relativity, was used to measure the Hubble constant using the gravitational-wave detection of the binary neutron-star merger, GW170817, by the Laser Interferometer Gravitational-Wave Observatory (LIGO) and Virgo4, combined with optical identification of the host galaxy5,6 NGC 4993. This independent measurement is of particular interest given the discrepancy between the value of the Hubble constant determined using type Ia supernovae via the local distance ladder (73.24 ± 1.74 kilometres per second per megaparsec) and the value determined from cosmic microwave background observations (67.4 ± 0.5 kilometres per second per megaparsec): these values differ7,8 by about 3σ. Local distance ladder observations may achieve a precision of one per cent within five years, but at present there are no indications that further observations will substantially reduce the existing discrepancies9. Here we show that additional gravitational-wave detections by LIGO and Virgo can be expected to constrain the Hubble constant to a precision of approximately two per cent within five years and approximately one per cent within a decade. This is because observing gravitational waves from the merger of two neutron stars, together with the identification of a host galaxy, enables a direct measurement of the Hubble constant independent of the systematics associated with other available methods. In addition to clarifying the discrepancy between existing low-redshift (local ladder) and high-redshift (cosmic microwave background) measurements, a precision measurement of the Hubble constant is of crucial value in elucidating the nature of dark energy10,11.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout


Similar content being viewed by others
References
Schutz, B. F. Determining the Hubble constant from gravitational wave observations. Nature 323, 310–311 (1986).
Holz, D. E. & Hughes, S. A. Using gravitational-wave standard sirens. Astrophys. J. 629, 15 (2005).
Dalal, N., Holz, D. E., Hughes, S. A. & Jain, B. Short GRB and binary black hole standard sirens as a probe of dark energy. Phys. Rev. D 74, 063006 (2006).
Abbott, B. P. et al. A gravitational-wave standard siren measurement of the Hubble constant. Nature 551, 85–88 (2017).
Coulter, D. A. et al. Swope Supernova Survey 2017a (SSS17a), the optical counterpart to a gravitational wave source. Science 358, 1556–1558 (2017).
Soares-Santos, M. et al. The electromagnetic counterpart of the binary neutron star merger LIGO/Virgo GW170817. I. Discovery of the optical counterpart using the dark energy camera. Astrophys. J. 848, L16 (2017).
Riess, A. G. et al. A 2.4% determination of the local value of the Hubble constant. Astrophys. J. 826, 56 (2016).
Aghanim, N. et al. Planck 2018 results. VI. Cosmological parameters. Preprint at https://arxiv.org/abs/1807.06209 (2018).
Riess, A. G. et al. New parallaxes of galactic Cepheids from spatially scanning the Hubble Space Telescope: implications for the Hubble constant. Astrophys. J. 855, 136 (2018).
Hu, W. Dark energy probes in light of the CMB. ASP Conf. Series 339, 215 (2005); preprint at https://arxiv.org/abs/astro-ph/0407158.
Di Valentino, E., Holz, D. E., Melchiorri, A. & Renzi, F. The cosmological impact of future constraints on H 0 from gravitational-wave standard sirens. Preprint at https://arxiv.org/abs/1806.07463 (2018).
Li, L.-X. & Paczyński, B. Transient events from neutron star mergers. Astrophys. J. 507, L59–L62 (1998).
Metzger, B. D. et al. Electromagnetic counterparts of compact object mergers powered by the radioactive decay of r-process nuclei. Mon. Not. R. Astron. Soc. 406, 2650–2662 (2010).
Fong, W. & Berger, E. The locations of short gamma-ray bursts as evidence for compact object binary progenitors. Astrophys. J. 776, 18 (2013).
Hirata, C. M., Holz, D. E. & Cutler, C. Reducing the weak lensing noise for the gravitational wave Hubble diagram using the non-Gaussianity of the magnification distribution. Phys. Rev. D 81, 124046 (2010).
Nissanke, S. et al. Determining the Hubble constant from gravitational wave observations of merging compact binaries. Preprint at https://arxiv.org/abs/1307.2638 (2013).
Abbott, B. P. et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101 (2017).
Abbott, B. P. et al. GW170104: observation of a 50-solar-mass binary black hole coalescence at redshift 0.2. Phys. Rev. Lett. 118, 221101 (2017).
Dominik, M. et al. Double compact objects III: gravitational-wave detection rates. Astrophys. J. 806, 263 (2015).
Belczynski, K. et al. Compact binary merger rates: comparison with LIGO/Virgo upper limits. Astrophys. J. 819, 108 (2016).
Belczynski, K., Holz, D. E., Bulik, T. & O’Shaughnessy, R. The first gravitational-wave source from the isolated evolution of two stars in the 40–100 solar mass range. Nature 534, 512–515 (2016).
Vitale, S. & Chen, H.-Y. Measuring the Hubble constant with neutron star black hole mergers. Phys. Rev. Lett. 121, 021303 (2018).
Guidorzi, C. et al. Improved constraints on H 0 from a combined analysis of gravitational-wave and electromagnetic emission from GW170817. Astrophys. J. 851, L36 (2017).
Karki, S. et al. The Advanced LIGO photon calibrators. Rev. Sci. Instrum. 87, 114503 (2016).
Holz, D. E. & Linder, E. V. Safety in numbers: gravitational lensing degradation of the luminosity distance-redshift relation. Astrophys. J. 631, 678–688 (2005).
Abbott, B. P. et al. The rate of binary black hole mergers inferred from advanced LIGO observations surrounding GW150914. Astrophys. J. 833, L1 (2016).
Fishbach, M. & Holz, D. E. Where are LIGO’s big black holes? Astrophys. J. 851, L25 (2017).
Chen, H.-Y. & Holz, D. E. Finding the one: identifying the host galaxies of gravitational-wave sources. Preprint at https://arxiv.org/abs/1612.01471 (2016).
Abbott, B. P. et al. Prospects for observing and localizing gravitational-wave transients with advanced LIGO and advanced Virgo. Liv. Rev. Rel. 19, 1 (2016).
Veitch, J. et al. Parameter estimation for compact binaries with ground-based gravitational-wave observations using the LALInference software library. Phys. Rev. D 91, 042003 (2015).
Carrick, J., Turnbull, S. J., Lavaux, G. & Hudson, M. J. Cosmological parameters from the comparison of peculiar velocities with predictions from the 2M++ density field. Mon. Not. R. Astron. Soc. 450, 317–332 (2015).
Scolnic, D. M. et al. The complete light-curve sample of spectroscopically confirmed type Ia supernovae from Pan-STARRS1 and cosmological constraints from the combined Pantheon sample. Astrophys. J. 859, 101 (2018).
Del Pozzo, W. Inference of cosmological parameters from gravitational waves: applications to second generation interferometers. Phys. Rev. D 86, 043011 (2012).
Fosalba, P., Crocce, M., Gaztañaga, E. & Castander, F. J. The MICE grand challenge lightcone simulation—I. Dark matter clustering. Mon. Not. R. Astron. Soc. 448, 2987–3000 (2015).
Crocce, M., Castander, F. J., Gaztañaga, E., Fosalba, P. & Carretero, J. The MICE Grand Challenge lightcone simulation—II. Halo and galaxy catalogues. Mon. Not. R. Astron. Soc. 453, 1513–1530 (2015).
Fosalba, P., Gaztañaga, E., Castander, F. J. & Crocce, M. The MICE Grand Challenge light-cone simulation—III. Galaxy lensing mocks from all-sky lensing maps. Mon. Not. R. Astron. Soc. 447, 1319–1332 (2015).
Carretero, J. et al. CosmoHub and SciPIC: massive cosmological data analysis, distribution and generation using a Big Data platform. In Proc. 2017 European Physical Society Conference on High Energy Physics 488 (EPS-HEP, 2017).
Schechter, P. An analytic expression for the luminosity function for galaxies. Astrophys. J. 203, 297–306 (1976).
Norberg, P. et al. The 2dF Galaxy Redshift Survey: the bJ-band galaxy luminosity function and survey selection function. Mon. Not. R. Astron. Soc. 336, 907–931 (2002).
Liske, J., Lemon, D. J., Driver, S. P., Cross, N. J. G. & Couch, W. J. The Millennium Galaxy Catalogue: 16 ≤ BMGC < 24 galaxy counts and the calibration of the local galaxy luminosity function. Mon. Not. R. Astron. Soc. 344, 307–324 (2003).
González, R. E., Lares, M., Lambas, D. G. & Valotto, C. The faint-end of the galaxy luminosity function in groups. Astron. Astrophys. 445, 51–58 (2006).
Kourkchi, E. & Tully, R. B. Galaxy groups within 3500 km s−1. Astrophys. J. 843, 16 (2017).
Chen, H.-Y. et al. Distance measures in gravitational-wave astrophysics and cosmology. Preprint at https://arxiv.org/abs/1709.08079 (2017).
Abbott, B. P. et al. Multi-messenger observations of a binary neutron star merger. Astrophys. J. 848, 12 (2017).
Schutz, B. F. Networks of gravitational wave detectors and three figures of merit. Class. Quant. Gravity 28, 125023 (2011).
Ade, P. A. R. et al. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 594, A13 (2016).
Acknowledgements
We acknowledge discussions with L. Blackburn, R. Essick, W. Farr and J. Gair. We were supported in part by NSF CAREER grant PHY-1151836 and NSF grant PHY-1708081. We were also supported by the Kavli Institute for Cosmological Physics at the University of Chicago through NSF grant PHY-1125897 and an endowment from the Kavli Foundation. We acknowledge the University of Chicago Research Computing Center for support of this work. H.-Y.C. was supported in part by the Black Hole Initiative at Harvard University, through a grant from the John Templeton Foundation. M.F. was supported by the NSF Graduate Research Fellowship Program under grant DGE-1746045.
Author contributions
H.-Y.C. led the project, conducted the simulations and led the analysis. M.F. provided the mathematical derivations and contributed to the analysis and results. D.E.H. conceived the project, supervised the research, and contributed to the analysis and results. All authors contributed to the draft preparation.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 H0 uncertainty for BNS systems with identified counterparts and redshifts.
Each point is the H0 uncertainty \({\sigma }_{{H}_{0}}\) from a simulated detection with the Advanced HLV network operating at design sensitivity, as a function of the 90% localization volume. The colours correspond to the median of the GW distance measurement. The lower limit to the precision of individual measurements of about 3 km s−1 Mpc−1 is due to the ‘sweet spot’ between peculiar velocities and distance uncertainties, as discussed in the text. We find that, in general, closer events have smaller localization volumes and lead to better constraints on H0, although the closest events yield slightly worse constraints because of their larger fractional peculiar velocity uncertainties.
Rights and permissions
About this article
Cite this article
Chen, HY., Fishbach, M. & Holz, D.E. A two per cent Hubble constant measurement from standard sirens within five years. Nature 562, 545–547 (2018). https://doi.org/10.1038/s41586-018-0606-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0606-0
Keywords
This article is cited by
-
Taiji-TianQin-LISA network: Precisely measuring the Hubble constant using both bright and dark sirens
Science China Physics, Mechanics & Astronomy (2024)
-
Synergy between CSST galaxy survey and gravitational-wave observation: Inferring the Hubble constant from dark standard sirens
Science China Physics, Mechanics & Astronomy (2024)
-
Cosmology with fast radio bursts in the era of SKA
Science China Physics, Mechanics & Astronomy (2023)
-
Cosmology with the Laser Interferometer Space Antenna
Living Reviews in Relativity (2023)
-
r-Process nucleosynthesis in gravitational-wave and other explosive astrophysical events
Nature Reviews Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.