Abstract
Wind-dispersed plants have evolved ingenious ways to lift their seeds1,2. The common dandelion uses a bundle of drag-enhancing bristles (the pappus) that helps to keep their seeds aloft. This passive flight mechanism is highly effective, enabling seed dispersal over formidable distances3,4; however, the physics underpinning pappus-mediated flight remains unresolved. Here we visualized the flow around dandelion seeds, uncovering an extraordinary type of vortex. This vortex is a ring of recirculating fluid, which is detached owing to the flow passing through the pappus. We hypothesized that the circular disk-like geometry and the porosity of the pappus are the key design features that enable the formation of the separated vortex ring. The porosity gradient was surveyed using microfabricated disks, and a disk with a similar porosity was found to be able to recapitulate the flow behaviour of the pappus. The porosity of the dandelion pappus appears to be tuned precisely to stabilize the vortex, while maximizing aerodynamic loading and minimizing material requirements. The discovery of the separated vortex ring provides evidence of the existence of a new class of fluid behaviour around fluid-immersed bodies that may underlie locomotion, weight reduction and particle retention in biological and manmade structures.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
The datasets generated and/or analysed during the current study are available from the corresponding author upon reasonable request.
References
Lentink, D., Dickson, W. B., van Leeuwen, J. L. & Dickinson, M. H. Leading-edge vortices elevate lift of autorotating plant seeds. Science 324, 1438–1440 (2009).
Greene, D. F. & Johnson, E. A. The aerodynamics of plumed seeds. Funct. Ecol. 4, 117–125 (1990).
Ridley, H. N. On the dispersal of seeds by wind. Ann. Bot. os-19, 351–364 (1905).
Small, J. The origin and development of the Compositæ. New Phytol. 17, 200–230 (1918).
Holm, L. G. World Weeds: Natural Histories and Distribution (John Wiley & Sons, New York, 1997).
Tackenberg, O., Poschlod, P. & Kahmen, S. Dandelion seed dispersal: the horizontal wind speed does not matter for long-distance dispersal—it is updraft! Plant Biol. 5, 451–454 (2003).
Sheldon, J. & Burrows, F. The dispersal effectiveness of the achene–pappus units of selected Compositae in steady winds with convection. New Phytol. 72, 665–675 (1973).
Nathan, R. et al. Mechanisms of long-distance seed dispersal. Trends Ecol. Evol. 23, 638–647 (2008).
Soons, M. B. & Ozinga, W. A. How important is long-distance seed dispersal for the regional survival of plant species? Divers. Distrib. 11, 165–172 (2005).
Greene, D. F. The role of abscission in long-distance seed dispersal by the wind. Ecology 86, 3105–3110 (2005).
Andersen, M. C. An analysis of variability in seed settling velocities of several wind-dispersed Asteraceae. Am. J. Bot. 79, 1087–1091 (1992).
Burrows, F. Calculation of the primary trajectories of plumed seeds in steady winds with variable convection. New Phytol. 72, 647–664 (1973).
Andersen, M. C. Diaspore morphology and seed dispersal in several wind-dispersed Asteraceae. Am. J. Bot. 80, 487–492 (1993).
Minami, S. & Azuma, A. Various flying modes of wind-dispersal seeds. J. Theor. Biol. 225, 1–14 (2003).
Sudo, S., Matsui, N., Tsuyuki, K. & Yano, T. Morphological design of dandelion. In Proc. 11th International Congress and Exposition (Society for Experimental Mechanics, 2008).
Tackenberg, O., Poschlod, P. & Bonn, S. Assessment of wind dispersal potential in plant species. Ecol. Monogr. 73, 191–205 (2003).
Stevenson, R. A., Evangelista, D. & Looy, C. V. When conifers took flight: a biomechanical evaluation of an imperfect evolutionary takeoff. Paleobiology 41, 205–225 (2015).
Délery, J. Three-Dimensional Separated Flows Topology: Singular Points, Beam Splitters and Vortex Structures (John Wiley & Sons, 2013).
Vogel, S. Life in Moving Fluids: The Physical Biology of Flow (Princeton Univ. Press, Princeton, 1981).
Barta, E. & Weihs, D. Creeping flow around a finite row of slender bodies in close proximity. J. Fluid Mech. 551, 1–17 (2006).
Casseau, V., De Croon, G., Izzo, D. & Pandolfi, C. Morphologic and aerodynamic considerations regarding the plumed seeds of Tragopogon pratensis and their implications for seed dispersal. PLoS ONE 10, e0125040 (2015).
Roos, F. W. & Willmarth, W. W. Some experimental results on sphere and disk drag. AIAA J. 9, 285–291 (1971).
Shenoy, A. & Kleinstreuer, C. Flow over a thin circular disk at low to moderate Reynolds numbers. J. Fluid Mech. 605, 253–262 (2008).
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502 (2007).
Cummins, C., Viola, I. M., Mastropaolo, E. & Nakayama, N. The effect of permeability on the flow past permeable disks at low Reynolds numbers. Phys. Fluids 29, 097103 (2017).
Vincent, L., Shambaugh, W. S. & Kanso, E. Holes stabilize freely falling coins. J. Fluid Mech. 801, 250–259 (2016).
Davidi, G. & Weihs, D. Flow around a comb wing in low-Reynolds-number flow. AIAA J. 50, 249–253 (2012).
Jones, S. K., Yun, Y. J. J., Hedrick, T. L., Griffith, B. E. & Miller, L. A. Bristles reduce the force required to ‘fling’ wings apart in the smallest insects. J. Exp. Biol. 219, 3759–3772 (2016).
Lee, S. H. & Kim, D. Aerodynamics of a translating comb-like plate inspired by a fairyfly wing. Phys. Fluids 29, 081902 (2017).
Santhanakrishnan, A. et al. Clap and fling mechanism with interacting porous wings in tiny insect flight. J. Exp. Biol. 217, 3898–3909 (2014).
Cheer, A. & Koehl, M. Paddles and rakes: fluid flow through bristled appendages of small organisms. J. Theor. Biol. 129, 17–39 (1987).
Ross, D. H. & Craig, D. A. Mechanisms of fine particle capture by larval black flies (Diptera: Simuliidae). Can. J. Zool. 58, 1186–1192 (1980).
van Duren, L. A. & Videler, J. J. Escape from viscosity: the kinematics and hydrodynamics of copepod foraging and escape swimming. J. Exp. Biol. 206, 269–279 (2003).
Seale, M., Cummins, C., Viola, I. M., Mastropaolo, E. & Nakayama, N. Design principles of hair-like structures as biological machines. J. R. Soc. Interface 15, 20180206 (2018).
Cummins, C., Nakayama, N., Viola, I. M. & Mastropaolo, E. MATLAB scripts for analysis of vortex shedding. https://doi.org/10.7488/ds/2362 (2018).
Viola, I. M., Nakayama, N., Mastropaolo, E. & Cummins, C. Vortex shedding in the wake of a 75% porous disk. https://doi.org/10.7488/ds/2363 (2018).
Dierick, M., Masschaele, B. & Hoorebeke, L. V. Octopus, a fast and user-friendly tomographic reconstruction package developed in LabView®. Meas. Sci. Technol. 15, 1366–1370 (2004).
R Core Team. R: A Language and Environment for Statistical Computing http://www.R-project.org/ (R Foundation for Statistical Computing, Vienna, Austria, 2013).
Sato, M., Bitter, I., Bender, M. A., Kaufman, A. E. & Nakajima, M. TEASAR: tree-structure extraction algorithm for accurate and robust skeletons. In Proc. 8th Pacific Conference on Computer Graphics and Applications (eds Barsky, B. A. et al.) 281–449 (IEEE, 2000).
Schneider, C. A., Rasband, W. S. & Eliceiri, K. W. NIH image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675 (2012).
Forster, B., Van De Ville, D., Berent, J., Sage, D. & Unser, M. Complex wavelets for extended depth-of-field: a new method for the fusion of multichannel microscopy images. Microsc. Res. Tech. 65, 33–42 (2004).
Preibisch, S., Saalfeld, S. & Tomancak, P. Globally optimal stitching of tiled 3D microscopic image acquisitions. Bioinformatics 25, 1463–1465 (2009).
White, C. M. The drag of cylinders in fluids at slow speeds. Proc. R. Soc. A 186, 472–479 (1946).
Chwang, A. T. & Wu, T. Y.-T. Hydromechanics of low-Reynolds-number flow. Part 2. Singularity method for Stokes flows. J. Fluid Mech. 67, 787–815 (1975).
Viola, I. M., Bot, P. & Riotte, M. On the uncertainty of CFD in sail aerodynamics. Int. J. Numer. Methods Fluids 72, 1146–1164 (2013).
Acknowledgements
This work was supported by the Leverhulme Trust (RPG-2015-255) and the Royal Society (UF140640). We thank I. Butler (Geosciences, University of Edinburgh) for assistance with the μCT scans; and A. Firth and M. Mason (Engineering, University of Edinburgh) for helping to build the wind tunnel.
Reviewer information
Nature thanks M. Dickinson and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
C.C., E.M., I.M.V. and N.N. designed the experiments. C.C. designed and set up the wind tunnel. C.C. carried out the numerical analyses, the flight assay and flow visualization with assistance from M.S. and D.C. C.C. designed and E.M. fabricated the silicon disks. A.M. optimized and performed the μCT scans, and M.S. analysed the resulting 3D images. C.C. wrote the manuscript; M.S., E.M., I.M.V. and N.N. helped with revision and editing. E.M., I.M.V. and N.N. designed and oversaw the project; I.M.V. supervised the investigations of fluid mechanics and N.N. supervised the biological and structural studies.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 SVR visualization of the wake of 10 fixed dandelion seeds.
The flow speed is half of the terminal velocity of the seed. Each image was obtained using long-exposure photography.
Extended Data Fig. 2 SVR visualization of the wake of 10 freely flying dandelion seeds.
a–j, Each image corresponds to a snapshot from a video of the flight of the dandelions in the wind tunnel. The images show the seeds as they pass through the laser sheet, and the SVR may be difficult to identify in some panels because of the orientation of the laser sheet with respect to the axis of the SVR.
Extended Data Fig. 3 The breakdown in symmetry in the SVR of dandelion seeds.
a, b, At low speeds, the SVR is axisymmetric. a, Contrast-enhanced image. b, Original image. c, d, At higher speeds, this symmetry is lost. c, Contrast-enhanced image. d, Original image. a–d, Experiments were repeated independently on n = 10 biological samples, with similar results. e, f, The axisymmetry of SVR at low Re (e) breaks down at higher Re (f).
Extended Data Fig. 4 Images of porous disks showing the resolution of the technique for disks of various porosities.
a, b, Impervious disk. c–f, A disk with 33% porosity. g, h, A disk with 55% porosity. i, j, A disk with 75% porosity. k–p, A disk with 89% porosity.
Extended Data Fig. 5 Steady and unsteady wake behind porous disks and pappi.
Video snapshots are shown. a–d, The flow visualization behind a solid disk, with a steady wake (a) and an unsteady wake at three time points within one period of vortex shedding (b–d). e–h, The flow around a porous disk (ε = 0.75) with a steady wake (e) and an unsteady wake at three time points within one period of vortex shedding (f–h). i–l, The wake behind a dandelion sample with a steady SVR (i) and at three time points within one period of vortex shedding (j–l).
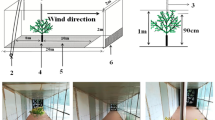
Extended Data Fig. 6 The experimental setup for laser Doppler anemometry and flow visualization.
a, b, Schematic drawings of the experimental setup for laser Doppler anemometry to measure the flow speed and turbulent intensity in the wind tunnel (a) and the experimental setup for flow visualization in the wind tunnel using a CW laser and high-speed camera (b). c, Photograph of the actual experimental setup for flow visualization.
Extended Data Fig. 7 Workflow for post-processing of the μCT scan data.
Image processing workflow for analysis of µCT data indicating the algorithms performed and the software used (Avizo or R).
Extended Data Fig. 8 The flow past a porous disk using direct numerical simulations and boundary integral methods.
a–c, The axial velocity uz/U (a), pressure p/ρU2 (b) and streamlines (c), showing the presence of an SVR with upstream and downstream stagnation points zsu and zsd, respectively. d, The reduction in the drag force on filaments within an array moving at slow speeds calculated using a boundary integral method. The force Di on the ith filament of a rectangular pappus, divided by the drag force for an isolated filament D0.
Supplementary information
Supplementary Information
This file contains Supplementary Discussions of the experiments (fixed and freely flying dandelions and porous disks) and further details of the microfabricated structures.
Supplementary Data
This file contains source data for the graphs in Figures 2-4, Extended Data Figure 8 and Extended Data Table 2.
Video 1
: SVR visualization in the wake of a freely flying dandelion seed. In this video, the dandelion seed is allowed to fly freely in the wind tunnel, and the SVR is visualized as the dandelion passes through the laser sheet. These experiments were repeated independently for n = 10 biological replicates with similar results.
Video 2
: SVR visualization in the wake of a fixed dandelion seed (low speed). In this video, the SVR is visualized by keeping the seed fixed in a low speed air flow. These experiments were repeated independently for n = 10 biological replicates with similar results.
Video 3
: SVR visualization in the wake of a fixed dandelion seed (high speed). In this video, the SVR is visualized by keeping the seed fixed in the air flow at terminal velocity. These experiments were repeated independently for n = 10 biological replicates with similar results.
Video 4
: SVR visualization in the wake of fixed disks of varying porosities. In this video, there are four panels. The bottom panels are visualizations of the flow past an impervious disk in steady (left) and unsteady (right) conditions. The top panels are visualizations of the flow past a porous disk (75% porous) in steady (left) and unsteady (right) conditions. Similar experiments were performed 15 times (each experiment had a different Reynolds number) for each disk with similar results.
Video 5
: SVR visualization in the wake of fixed disks of varying porosities (high porosity). In this video, there are four panels. The bottom panels are visualizations of the flow past a porous disk (89% porous) in steady (left) and unsteady (right) conditions. The top panels are visualizations of the flow past a porous disk (92% porous) in steady (left) and unsteady (right) conditions. Similar experiments were performed 20 and 17 times (each experiment had a different Reynolds number) for the 89% and 92% porous disks respectively with similar results.
Rights and permissions
About this article
Cite this article
Cummins, C., Seale, M., Macente, A. et al. A separated vortex ring underlies the flight of the dandelion. Nature 562, 414–418 (2018). https://doi.org/10.1038/s41586-018-0604-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0604-2
Keywords
This article is cited by
-
Light-driven dandelion-inspired microfliers
Nature Communications (2023)
-
Geometric descriptors for the prediction of snowflake drag
Experiments in Fluids (2023)
-
Identifying dominant flow features from very-sparse Lagrangian data: a multiscale recurrence network-based approach
Experiments in Fluids (2023)
-
Dynamic wake behind a dandelion pappus: PIV and smoke-wire visualization
Journal of Visualization (2023)
-
“Phoenix in Flight”: an unique fruit morphology ensures wind dispersal of seeds of the phoenix tree (Firmiana simplex (L.) W. Wight)
BMC Plant Biology (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.