Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

A topological source of quantum light

Nature volume 561, pages 502–506 (2018)Cite this article

Subjects

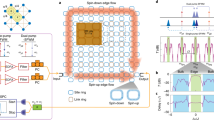
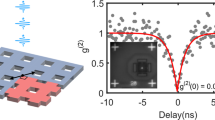
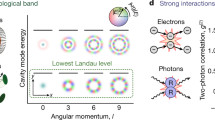
Abstract

Quantum light is characterized by distinctive statistical distributions that are possible only because of quantum mechanical effects. For example, single photons and correlated photon pairs exhibit photon number distributions with variance lower than classically allowed limits. This enables high-fidelity transmission of quantum information and sensing with lower noise than possible with classical light sources1,2. Most quantum light sources rely on spontaneous parametric processes such as down-conversion and four-wave mixing2. These processes are mediated by vacuum fluctuations of the electromagnetic field. Therefore, by manipulating the electromagnetic mode structure, for example with dispersion-engineered nanophotonic systems, the spectrum of generated photons can be controlled3,4,5,6,7. However, disorder, which is ubiquitous in nanophotonic fabrication, causes device-to-device spectral variations8,9,10,11. Here we realize topologically robust electromagnetic modes and use their vacuum fluctuations to create a quantum light source in which the spectrum of generated photons is much less affected by fabrication-induced disorder. Specifically, we use the topological edge states realized in a two-dimensional array of ring resonators to generate correlated photon pairs by spontaneous four-wave mixing and show that they outperform their topologically trivial one-dimensional counterparts in terms of spectral robustness. We demonstrate the non-classical nature of the generated light and the realization of a robust source of heralded single photons by measuring the conditional antibunching of photons, that is, the reduced likelihood of photons arriving together compared to thermal or laser light. Such topological effects, which are unique to bosonic systems, could pave the way for the development of robust quantum photonic devices.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Schematic of the experimental set-up.
Fig. 2: Spectral distribution of the generated photons.
Fig. 3: Source characterization.
Fig. 4: Robustness of spectral correlations between pump and signal photons.
Fig. 5: Similarity scaling as a function of device size.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author on reasonable request.

References

  1. Shields, A. J. Semiconductor quantum light sources. Nat. Photon. 1, 215–223 (2007).

    Article  ADS  CAS  Google Scholar 

  2. Eisaman, M. D., Fan, J., Migdall, A. & Polyakov, S. V. Single-photon sources and detectors. Rev. Sci. Instrum. 82, 071101 (2011).

    Article  ADS  CAS  Google Scholar 

  3. Sharping, J. E. et al. Generation of correlated photons in nanoscale silicon waveguides. Opt. Express 14, 12388–12393 (2006).

    Article  ADS  Google Scholar 

  4. Clemmen, S. et al. Continuous wave photon pair generation in silicon-on-insulator waveguides and ring resonators. Opt. Express 17, 16558–16570 (2009).

    Article  ADS  CAS  Google Scholar 

  5. Förtsch, M. et al. A versatile source of single photons for quantum information processing. Nat. Commun. 4, 1818 (2013).

    Article  Google Scholar 

  6. Davanço, M. et al. Telecommunications-band heralded single photons from a silicon nanophotonic chip. Appl. Phys. Lett. 100, 261104 (2012).

    Article  ADS  Google Scholar 

  7. Kumar, R., Ong, J. R., Savanier, M. & Mookherjea, S. Controlling the spectrum of photons generated on a silicon nanophotonic chip. Nat. Commun. 5, 5489 (2014).

    Article  ADS  CAS  Google Scholar 

  8. Topolancik, J., Ilic, B. & Vollmer, F. Experimental observation of strong photon localization in disordered photonic crystal waveguides. Phys. Rev. Lett. 99, 253901 (2007).

    Article  ADS  CAS  Google Scholar 

  9. Mookherjea, S., Park, J. S., Yang, S.-H. & Bandaru, P. R. Localization in silicon nanophotonic slow-light waveguides. Nat. Photon. 2, 90–93 (2008).

    Article  ADS  CAS  Google Scholar 

  10. Sapienza, L. et al. Cavity quantum electrodynamics with anderson-localized modes. Science 327, 1352–1355 (2010).

    Article  ADS  CAS  Google Scholar 

  11. Spring, J. B. et al. Chip-based array of near-identical, pure, heralded single-photon sources. Optica 4, 90–96 (2017).

    Article  Google Scholar 

  12. Morichetti, F. et al. Travelling-wave resonant four-wave mixing breaks the limits of cavity-enhanced all-optical wavelength conversion. Nat. Commun. 2, 296 (2011).

    Article  Google Scholar 

  13. Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).

    Article  ADS  CAS  Google Scholar 

  14. Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljačić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    Article  ADS  CAS  Google Scholar 

  15. Hafezi, M., Demler, E. A., Lukin, M. D. & Taylor, J. M. Robust optical delay lines with topological protection. Nat. Phys. 7, 907–912 (2011).

    Article  CAS  Google Scholar 

  16. Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).

    Article  ADS  CAS  Google Scholar 

  17. Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013).

    Article  ADS  CAS  Google Scholar 

  18. Chen, W.-J. et al. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 5, 5782 (2014).

    Article  CAS  Google Scholar 

  19. Cheng, X. et al. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 15, 542–548 (2016).

    Article  ADS  CAS  Google Scholar 

  20. Kraus, Y., Lahini, Y., Ringel, Z., Verbin, M. & Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012).

    Article  ADS  Google Scholar 

  21. Hafezi, M. Measuring topological invariants in photonic systems. Phys. Rev. Lett. 112, 210405 (2014).

    Article  ADS  Google Scholar 

  22. Mittal, S., Ganeshan, S., Fan, J., Vaezi, A. & Hafezi, M. Measurement of topological invariants in a 2D photonic system. Nat. Photon. 10, 180–183 (2016).

    Article  ADS  CAS  Google Scholar 

  23. Mittal, S. et al. Topologically robust transport of photons in a synthetic gauge field. Phys. Rev. Lett. 113, 087403 (2014).

    Article  ADS  CAS  Google Scholar 

  24. St-Jean, P. et al. Lasing in topological edge states of a one-dimensional lattice. Nat. Photon. 11, 651–656 (2017).

    Article  ADS  CAS  Google Scholar 

  25. Bahari, B. et al. Nonreciprocal lasing in topological cavities of arbitrary geometries. Science 358, 636–640 (2017).

    Article  ADS  CAS  Google Scholar 

  26. Peano, V., Houde, M., Marquardt, F. & Clerk, A. A. Topological quantum fluctuations and traveling wave amplifiers. Phys. Rev. X 6, 041026 (2016).

    Google Scholar 

  27. Shi, T., Kimble, H. J. & Cirac, J. I. Topological phenomena in classical optical networks. Proc. Natl Acad. Sci. USA 114, E8967–E8976 (2017).

    Article  ADS  MathSciNet  CAS  Google Scholar 

  28. Chen, J., Levine, Z. H., Fan, J. & Migdall, A. L. Frequency-bin entangled comb of photon pairs from a silicon-on-insulator micro-resonator. Opt. Express 19, 1470–1483 (2011).

    Article  ADS  CAS  Google Scholar 

  29. Ong, J. R. & Mookherjea, S. Quantum light generation on a silicon chip using waveguides and resonators. Opt. Express 21, 5171–5181 (2013).

    Article  ADS  CAS  Google Scholar 

  30. Yariv, A., Xu, Y., Lee, R. K. & Scherer, A. Coupled-resonator optical waveguide: a proposal and analysis. Opt. Lett. 24, 711–713 (1999).

    Article  ADS  CAS  Google Scholar 

  31. Bauters, J. F. et al. Ultra-low-loss high-aspect-ratio Si3N4 waveguides. Opt. Express 19, 3163–3174 (2011).

    Article  ADS  CAS  Google Scholar 

  32. Moss, D. J., Morandotti, R., Gaeta, A. L. & Lipson, M. New CMOS-compatible platforms based on silicon nitride and hydex for nonlinear optics. Nat. Photon. 7, 597–607 (2013).

    Article  ADS  CAS  Google Scholar 

Download references

Acknowledgements

This research was supported by AFOSR-MURI FA9550-14-1-0267, YIP-ONR, Sloan Foundation and the Physics Frontier Center at the Joint Quantum Institute. We thank V. V. Orre for help with the experimental set-up, A. Karasahin for help with the SEM, T. Huber and D. Englund for discussions and Q. Quraishi for providing the nanowire detectors.

Reviewer information

Nature thanks V. Peano and the other anonymous reviewer(s) for their contribution to the peer review of this work.

Author information

Authors and Affiliations

  1. Joint Quantum Institute, NIST/University of Maryland, College Park, MD, USA

    Sunil Mittal, Elizabeth A. Goldschmidt & Mohammad Hafezi

  2. IREAP/Department of Electrical and Computer Engineering, University of Maryland, College Park, MD, USA

    Sunil Mittal & Mohammad Hafezi

  3. US Army Research Laboratory, Adelphi, MD, USA

    Elizabeth A. Goldschmidt

  4. Department of Physics, University of Maryland, College Park, MD, USA

    Mohammad Hafezi

Authors
  1. Sunil Mittal
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Elizabeth A. Goldschmidt
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mohammad Hafezi
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.M. and M.H. conceived the idea. S.M. performed the numerical simulations and the experimental measurements. E.A.G. contributed to source characterization. M.H. supervised the project. All authors contributed to analysing the data and writing the manuscript.

Corresponding author

Correspondence to Sunil Mittal.

Ethics declarations

Competing interests

The authors declare no competing interests.

Additional information

Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

Extended Data Fig. 1 Spectral correlations.

a–c, Measured Γ(ωs, ωp) on three different 2D devices; d–g, measured Γ(ωs, ωp) on four different 1D devices, in addition to those presented in Fig. 3. Clockwise edge bands for the 2D devices and mid-band for the 1D devices are highlighted.

Extended Data Fig. 2 Transmission spectra of 2D and 1D devices.

a, b, Measured transmission spectra for (a) different 2D and (b) different 1D devices. The shaded regions highlight the edge and the bulk bands for the 2D system and the mid-band for the 1D system. For the 2D devices, the clockwise and the anticlockwise edge bands show reduced variations in the transmission compared with that in the bulk band. These spectra have been shifted along the frequency axis to superpose them, using an algorithm based on transmission and delay measurements, as detailed in ref. 23.

Extended Data Fig. 3 Transmission spectrum of a 2D device across three FSRs.

Measured transmission spectrum in the pump, signal and idler FSRs, corresponding to Fig. 2. ∆ν is the frequency relative to the longitudinal mode resonance, and Ω is the FSR. The shape of the transmission spectrum in these FSRs is almost identical. The small variation in the overall transmission across bands is mainly because of the frequency response of the grating couplers.

Extended Data Fig. 4 Joint spectral intensity.

a, The measured Γ(ωs, ωp) (see Fig. 2): that is, the intensity of generated signal photons at frequency ωs as a function of pump frequency, ωp. Each point on this plot represents a particular ωs and ωp. Using energy conservation, we can calculate the corresponding idler frequency at each point as ωi = 2ωp − ωs. Therefore, we can easily rescale the y axis of the plot and calculate the joint-spectral intensity (JSI; see refs 11,29) between the signal and idler frequencies, as shown in b. Note that this rescaling works only for a continuous-wave pump because for a pulsed pump source, the above energy conservation relation holds only up to the spectral bandwidth of the pump, signal and idler photons. Also, this measurement inherently assumes that the generated signal and idler photons are correlated. Using CAR and direct measurements of the signal and idler spectra (in Figs. 2, 3), we verified that the signal and idler photons are indeed correlated. The main advantage of such a spectral correlation measurement between the pump and the signal (or idler) photons is that it is fast and, for a continuous-wave pump, is equivalent to the JSI measurement.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mittal, S., Goldschmidt, E.A. & Hafezi, M. A topological source of quantum light. Nature 561, 502–506 (2018). https://doi.org/10.1038/s41586-018-0478-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41586-018-0478-3

Keywords

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing