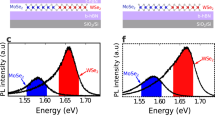
Abstract
Devices that rely on the manipulation of excitons—bound pairs of electrons and holes—hold great promise for realizing efficient interconnects between optical data transmission and electrical processing systems. Although exciton-based transistor actions have been demonstrated successfully in bulk semiconductor-based coupled quantum wells1,2,3, the low temperature required for their operation limits their practical application. The recent emergence of two-dimensional semiconductors with large exciton binding energies4,5 may lead to excitonic devices and circuits that operate at room temperature. Whereas individual two-dimensional materials have short exciton diffusion lengths, the spatial separation of electrons and holes in different layers in heterostructures could help to overcome this limitation and enable room-temperature operation of mesoscale devices6,7,8. Here we report excitonic devices made of MoS2–WSe2 van der Waals heterostructures encapsulated in hexagonal boron nitride that demonstrate electrically controlled transistor actions at room temperature. The long-lived nature of the interlayer excitons in our device results in them diffusing over a distance of five micrometres. Within our device, we further demonstrate the ability to manipulate exciton dynamics by creating electrically reconfigurable confining and repulsive potentials for the exciton flux. Our results make a strong case for integrating two-dimensional materials in future excitonic devices to enable operation at room temperature.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
High, A. A., Hammack, A. T., Butov, L. V., Hanson, M. & Gossard, A. C. Exciton optoelectronic transistor. Opt. Lett. 32, 2466–2468 (2007).
High, A. A., Novitskaya, E. E., Butov, L. V., Hanson, M. & Gossard, A. C. Control of exciton fluxes in an excitonic integrated circuit. Science 321, 229–231 (2008).
Grosso, G. et al. Excitonic switches operating at around 100 K. Nat. Photon. 3, 577–580 (2009).
Cheiwchanchamnangij, T. & Lambrecht, W. R. L. Quasiparticle band structure calculation of monolayer, bilayer, and bulk MoS2. Phys. Rev. B 85, 205302 (2012).
He, K. et al. Tightly bound excitons in monolayer WSe2. Phys. Rev. Lett. 113, 026803 (2014).
Rivera, P. et al. Observation of long-lived interlayer excitons in monolayer MoSe2–WSe2 heterostructures. Nat. Commun. 6, 6242 (2015).
Palummo, M., Bernardi, M. & Grossman, J. C. Exciton radiative lifetimes in two-dimensional transition metal dichalcogenides. Nano Lett. 15, 2794–2800 (2015).
Miller, B. et al. Long-lived direct and indirect interlayer excitons in van der Waals heterostructures. Nano Lett. 17, 5229–5237 (2017).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Miller, D. A. B. Rationale and challenges for optical interconnects to electronic chips. Proc. IEEE 88, 728–749 (2000).
Butov, L. V. Excitonic devices. Superlattices Microstruct. 108, 2–26 (2017).
Liu, A. et al. A high-speed silicon optical modulator based on a metal–oxide–semiconductor capacitor. Nature 427, 615–618 (2004).
Melikyan, A. et al. High-speed plasmonic phase modulators. Nat. Photon. 8, 229–233 (2014).
Xu, Q., Schmidt, B., Pradhan, S. & Lipson, M. Micrometre-scale silicon electro-optic modulator. Nature 435, 325–327 (2005).
Schmidt, B., Xu, Q., Shakya, J., Manipatruni, S. & Lipson, M. Compact electro-optic modulator on silicon-on-insulator substrates using cavities with ultra-small modal volumes. Opt. Express 15, 3140–3148 (2007).
Fedichkin, F. et al. Room-temperature transport of indirect excitons in AlGaN/GaN quantum wells. Phys. Rev. Appl. 6, 014011 (2016).
Kuznetsova, Y. Y. et al. Transport of indirect excitons in ZnO quantum wells. Opt. Lett. 40, 3667–3670 (2015).
Fogler, M. M., Butov, L. V. & Novoselov, K. S. High-temperature superfluidity with indirect excitons in van der Waals heterostructures. Nat. Commun. 5, 4555 (2014).
Robert, C. et al. Exciton radiative lifetime in transition metal dichalcogenide monolayers. Phys. Rev. B 93, 205423 (2016).
Kang, J., Tongay, S., Zhou, J., Li, J. & Wu, J. Band offsets and heterostructures of two-dimensional semiconductors. Appl. Phys. Lett. 102, 012111 (2013).
Chiu, M.-H. et al. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 6, 7666 (2015).
Fang, H. et al. Strong interlayer coupling in van der Waals heterostructures built from single-layer chalcogenides. Proc. Natl Acad. Sci. USA 111, 6198–6202 (2014).
Kunstmann, J. et al. Momentum-space indirect interlayer excitons in transition-metal dichalcogenide van der Waals heterostructures. Nat. Phys. https://doi.org/10.1038/s41567-018-0123-y (2018).
Kim, J. et al. Observation of ultralong valley lifetime in WSe2/MoS2 heterostructures. Sci. Adv. 3, e1700518 (2017).
Cadiz, F. et al. Exciton diffusion in WSe2 monolayers embedded in a van der Waals heterostructure. Appl. Phys. Lett. 112, 152106 (2018).
Kulig, M. et al. Exciton diffusion and halo effects in monolayer semiconductors. Phys. Rev. Lett. 120, 207401 (2018).
Onga, M., Zhang, Y., Ideue, T. & Iwasa, Y. Exciton Hall effect in monolayer MoS2. Nat. Mater. 16, 1193–1197 (2017).
Nagler, P. et al. Interlayer exciton dynamics in a dichalcogenide monolayer heterostructure. 2D Mater. 4, 025112 (2017).
Wang, R. et al. Ultrafast and spatially resolved studies of charge carriers in atomically thin molybdenum disulfide. Phys. Rev. B 86, 045406 (2012).
Mayorov, A. S. et al. Micrometer-scale ballistic transport in encapsulated graphene at room temperature. Nano Lett. 11, 2396–2399 (2011).
Zhu, H. et al. Interfacial charge transfer circumventing momentum mismatch at two-dimensional van der Waals heterojunctions. Nano Lett. 17, 3591–3598 (2017).
Schneider, C. A., Rasband, W. S. & Eliceiri, K. W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675 (2012).
Acknowledgements
We are grateful to K. Marinov and D. Ovchinnikov for discussion. We acknowledge the help of Z. Benes (CMI) with electron-beam lithography. D.U., A.C., A.A. and A.K. acknowledge support by the Swiss National Science Foundation (grant 153298), H2020 European Research Council (ERC, grant 682332) and Marie Curie-Sklodowska-Curie Actions (COFUND grant 665667). A.K. acknowledges funding from the European Union’s Horizon H2020 Future and Emerging Technologies under grant agreement number 696656 (Graphene Flagship). K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and JSPS KAKENHI grant numbers JP15K21722 and JP25106006.
Reviewer information
Nature thanks W. Gao, A. Tartakovskii and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Author information
Authors and Affiliations
Contributions
A.C. and A.A. fabricated the devices, D.U. and A.C. performed the optical measurements and analysed the data. K.W. and T.T. grew the h-BN crystals. A.K. initiated and supervised the project. D.U., A.C., A.A. and A.K. wrote the manuscript with input from all authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Interlayer excitons in the WSe2–MoS2 van der Waals heterostructure.
a, Spatial map of photoluminescence at 785 nm corresponding to the heterostructure interlayer photoluminescence emission maximum, as shown in the photoluminescence (PL) spectra in b. An efficient interlayer charge-transfer process in the heterostructure encapsulated in h-BN results in further quenching of photoluminescence emission from the heterostructure. Scale bar, 5 μm. b, Photoluminescence spectra from the structure fabricated on SiO2.
Extended Data Fig. 2 Spectra of excitonic device emission.
a, Distribution of photoluminescence emission intensity from the device, in the absence of an electric field. White dashed lines represent edges of constituent crystals. Scale bar, 5 μm. b, Detailed spectrum of the emission pattern, showing the interlayer exciton peak (Xi) and WSe2 intralayer emission. We note that the low-energy peak (Xi) cannot be related to localized excitons in WSe2, because they are observed only at cryogenic temperatures. c, Full spectrum of the emission shown in a, also showing the emission from MoS2 (\({X}_{0}^{{{\rm{MoS}}}_{2}}\)), which is blocked by the filter in the CCD image. The black dashed box indicates the range of energies shown in b.
Extended Data Fig. 3 Characterization of an additional WSe2–MoS2 heterostructure.
a, False-colour optical image of the fabricated stack. b, Atomic force microscopy (AFM) height-profile image of the heterostructure. c–e, Spatial maps of photoluminescence intensity at emission wavelengths (λ) of 670 nm (c), 750 nm (d) and 785 nm (e), corresponding to MoS2 intralayer (X0), WSe2 intralayer (X0) and heterostructure interlayer (Xi) excitonic resonances. Photoluminescence is quenched in the heterostructure area owing to efficient charge transfer. White dashed lines represent edges of constituent crystals. Scale bars, 5 μm.
Extended Data Fig. 4 Excitonic transistor input and output.
a, Cross-sectional profile of the device emission intensity along the white dashed lines in b and c, obtained for different gate voltages Vg1 from 0 V (light blue) to 16 V (black) with intermediate values of 4 V, 6 V and 8 V. The red line represents the intensity profile of the laser spot. b, c, CCD images of the exciton emission in the ON state (b) and of the focused laser spot (c). The lengths of the dashed lines indicate 10 μm.
Extended Data Fig. 5 Switching of the excitonic transistor.
a–f, CCD images of exciton emission from the device, obtained for different gate voltages Vg1 from 0 to 10 V in steps of 2 V.
Extended Data Fig. 6 Spectrum of light emitted from the device in different states.
a, b, Intensity distribution of light emission from the excitonic transistor in the OFF and ON states (left and right, respectively; a) and the corresponding spectra collected from the entire device (black and red, respectively; b). c, d, Intensity distribution of light emission from the excitonic device in the confinement and expulsion configurations (left and right, respectively; c) and the corresponding spectra collected from the entire device (blue and red, respectively; d).
Extended Data Fig. 7 Schematic depiction of the control over the light emission.
a, b, Energy profiles for electrons (red) and holes (blue) in the device when applying negative (a) or positive (b) voltage on the central gate (Vg2). c, d, Corresponding expected emission images under the single-particle assumption. e, f, Energy profiles of interlayer excitons (ILE) in the presence of an external electric field, under the same conditions as in a and b. g, h, Corresponding experimental results. Scale bar, 5 μm. The figures in a–d are schematics based on the hypothesis that after the fast interlayer charge transfer, photo-excited carriers move independently rather than being bound in interlayer excitons. The diffusion of single electrons and holes is then subject to the type-II band alignment between MoS2 and WSe2, which restricts the motion of electrons to MoS2 and holes to WSe2. This charge separation is very efficient, as indicated by the strong suppression of intralayer emission from the heterostructure (Fig. 1e, f). Once the separation occurs, it is not very likely that the charges can hop between the layers: the band difference between MoS2 and WSe2 is more than 200 meV, so thermal excitation of 25 meV will not be enough for electrons to jump back to WSe2 and holes to jump back to MoS2. Another thing to consider is the local electrostatic potential defined by the gate. The application of Vg2 < 0 creates a confining energy profile for single holes and a repulsive one for single electrons, as in a and c. Holes would then be confined in the WSe2 area under the gate while electrons would be pushed out to MoS2 areas next to the gate, where they would recombine with charges already present in the monolayer area, resulting in photoluminescence from single-layer areas of MoS2 next to the gate (provided that there are enough holes in MoS2 to start with). We would then expect to obtain the emission pattern shown in c, assuming the presence of native holes in MoS2. In their absence, we would expect to see only one emission spot, coinciding with the excitation laser spot. Along the same lines, applying a positive gate voltage to the middle gate (Vg2 > 0) would result in a repulsive potential for holes in WSe2 and an attractive one for electrons in MoS2. Recombination would then occur for electrons in MoS2 in regions under the gate and for holes in WSe2 in regions outside the gate, as shown in d. This is in contradiction with the experimental observations in e–h. In the case of interlayer exciton transport, we instead have only a single energy profile (e, g), and the application of a positive voltage on the middle gate results in the expulsion of interlayer excitons from the injection region (f, h).
Extended Data Fig. 8 Excitonic transistor characterization for different positions of the excitation laser spot.
a, Normalized emission intensity (transistor output) as a function of the distance between optical injection and the emission point di–o, which is the same as in Fig. 3c, shown for the ON (blue, Vg1 = 0 V) and OFF (black, Vg1 = 16 V) states. b, Transistor efficiency calculated as the ratio between output emission in the ON and OFF states for different input–output separation distances di–o. Efficiency reaches a maximum when the laser spot is moved completely beyond the gate, so that the energy barrier stays between the input and the output and thus effectively modulates exciton diffusion.
Extended Data Fig. 9 Characterization of the device at low temperatures.
a, Normalized output intensity as a function of the distance between optical injection and emission points, obtained at room temperature (red, 300 K) and 4.7 K (blue). No electric field is applied. b, Emission images of the device in the ON (top) and OFF (down) states when measured at 4.7 K, with input–output separations as long as di–o = 5.1 μm. Such long-distance transistor switching was not observed at room temperature for this sample.
Extended Data Fig. 10 Heterostructure fabrication.
Optical images taken during different fabrication steps: a, exfoliation of the bottom h-BN (b-hBN); b, transfer of a monolayer MoS2 flake; c, transfer of a monolayer WSe2 flake; d, encapsulation with top h-BN (t-hBN); e, transfer of pre-patterned few-layer graphene stripes (Gr); and f, metallization of Au/Ti contacts. The image in e is shown in black and white for better visibility of the final structure. Scale bar, 10 μm (applies to all images).
Extended Data Fig. 11 Variation in photoluminescence emission from MoS2 due to the inhomogeneity of the substrate.
a, Image of photoluminescence emission coming from the device in the repulsive configuration shown in Fig. 4f. b, Micro-photoluminescence (μPL) spectra from the areas marked by red and blue circles in a, showing different peak widths as a result of local inhomogeneity in the heterostructure. The grey shaded area is the part of the spectrum cut by the 700-nm long-pass filter. As can be clearly seen in the image, areas where MoS2 photoluminescence shows a low-energy tail due to broadening become visible to the CCD (left side of the device), whereas the other areas appear dark (right side).
Extended Data Fig. 12 Reference experiments.
a, Photoluminescence spectra from monolayer WSe2 at different back-gate voltages. Substantial modulation of the emission intensity is observed. b, Photoluminescence spectra from monolayer WSe2 when using top and back gates in the dual-gated configuration, for the voltage range used in the experiment presented in Fig. 2. No appreciable intensity modulation is observed. Both measurements are performed on the same WSe2 flake with the same continuous-wave excitation at 647 nm and 200 μW of incident power.
Extended Data Fig. 13 Image post-processing.
a, Original CCD image of the exciton emission for the configuration shown in Fig. 3a. The yellow square highlights the area of interest, shown in Fig. 3c. b, The same image after background subtraction. c, Original CCD image of the exciton emission for the configuration shown in Fig. 3b. d, The same image after background subtraction. Scale bars, 15 μm.
Extended Data Fig. 14 Modelling of exciton diffusion.
Schematic of exciton generation in the pumping area (x < 0) and diffusion outside (x > 0), represented by the exciton concentration n(x). Constant pumping by the laser (red area) is determined by the generation rate G. This rate together with the recombination rate R establish the exciton concentration n0 in the pumping region. The concentration gradient outside the pumping area generates an exciton flux jdiff that drives diffusion and leads to the exponential decay of exciton concentration along the x axis.
Extended Data Fig. 15 Numerical simulation of the interlayer exciton in an external field.
a, Two-dimensional cross-sectional map of the electric-field amplitude calculated for the device in the exciton confinement configuration, with −10 V applied to the central gate and the side gates grounded. b, Corresponding amplitude of the vertical electric field (black, left axis) and the electrostatic potential (red, right axis) along the heterobilayer. c, Energy shift experienced by an interlayer exciton (black, ILE) and a single hole (red, multiplied by 300) along the same cross-section. d, Projection along the x axis of the confinement force experienced by the interlayer exciton owing to the presence of the electric field. Blue arrows show the direction of the force.
Rights and permissions
About this article
Cite this article
Unuchek, D., Ciarrocchi, A., Avsar, A. et al. Room-temperature electrical control of exciton flux in a van der Waals heterostructure. Nature 560, 340–344 (2018). https://doi.org/10.1038/s41586-018-0357-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0357-y
This article is cited by
-
Ultraviolet interlayer excitons in bilayer WSe2
Nature Nanotechnology (2024)
-
Room-temperature quantum emission from interface excitons in mixed-dimensional heterostructures
Nature Communications (2024)
-
Observation of possible excitonic charge density waves and metal–insulator transitions in atomically thin semimetals
Nature Physics (2024)
-
Excitonic devices based on two-dimensional transition metal dichalcogenides van der Waals heterostructures
Frontiers of Chemical Science and Engineering (2024)
-
Recent progress of exciton transport in two-dimensional semiconductors
Nano Convergence (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.