Abstract
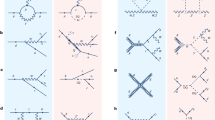
Large experimental programmes in the fields of nuclear and particle physics search for evidence of physics beyond that explained by current theories. The observation of the Higgs boson completed the set of particles predicted by the standard model, which currently provides the best description of fundamental particles and forces. However, this theory’s limitations include a failure to predict fundamental parameters, such as the mass of the Higgs boson, and the inability to account for dark matter and energy, gravity, and the matter–antimatter asymmetry in the Universe, among other phenomena. These limitations have inspired searches for physics beyond the standard model in the post-Higgs era through the direct production of additional particles at high-energy accelerators, which have so far been unsuccessful. Examples include searches for supersymmetric particles, which connect bosons (integer-spin particles) with fermions (half-integer-spin particles), and for leptoquarks, which mix the fundamental quarks with leptons. Alternatively, indirect searches using precise measurements of well predicted standard-model observables allow highly targeted alternative tests for physics beyond the standard model because they can reach mass and energy scales beyond those directly accessible by today’s high-energy accelerators. Such an indirect search aims to determine the weak charge of the proton, which defines the strength of the proton’s interaction with other particles via the well known neutral electroweak force. Because parity symmetry (invariance under the spatial inversion (x, y, z) → (−x, −y, −z)) is violated only in the weak interaction, it provides a tool with which to isolate the weak interaction and thus to measure the proton’s weak charge1. Here we report the value 0.0719 ± 0.0045, where the uncertainty is one standard deviation, derived from our measured parity-violating asymmetry in the scattering of polarized electrons on protons, which is −226.5 ± 9.3 parts per billion (the uncertainty is one standard deviation). Our value for the proton’s weak charge is in excellent agreement with the standard model2 and sets multi-teraelectronvolt-scale constraints on any semi-leptonic parity-violating physics not described within the standard model. Our results show that precision parity-violating measurements enable searches for physics beyond the standard model that can compete with direct searches at high-energy accelerators and, together with astronomical observations, can provide fertile approaches to probing higher mass scales.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
22 May 2018
In the originally published article, equation (6) was corrupted. This has now been corrected.
References
Erler, J., Kurylov, A. & Ramsey-Musolf, M. J. Weak charge of the proton and new physics. Phys. Rev. D 68, 016006 (2003).
Particle Data Group. Review of particle physics. Chinese Phys. C 40, 100001 (2016).
Androić, D. et al. First determination of the weak charge of the proton. Phys. Rev. Lett. 111, 141803 (2013).
Allison, T. et al. The Q weak experimental apparatus. Nucl. Instrum. Meth. A 781, 105–133 (2015).
Narayan, A. et al. Precision electron-beam polarimetry at 1 GeV using diamond microstrip detectors. Phys. Rev. X 6, 011013 (2016).
Smith, G. R. The Q weak target performance. Nuovo Cim. C 35, 159–163 (2012).
Young, R. D., Roche, J., Carlini, R. D. & Thomas, A. W. Extracting nucleon strange and anapole form factors from world data. Phys. Rev. Lett. 97, 102002 (2006).
Young, R. D., Carlini, R. D., Thomas, A. W. & Roche, J. Testing the standard model by precision measurement of the weak charges of quarks. Phys. Rev. Lett. 99, 122003 (2007).
Arrington, J. & Sick, I. Precise determination of low-Q nucleon electromagnetic form factors and their impact on parity-violating e-p elastic scattering. Phys. Rev. C 76, 035201 (2007).
Hall, N. L., Blunden, P. G., Melnitchouk, W., Thomas, A. W. & Young, R. D. Quark-hadron duality constraints on γZ box corrections to parity-violating elastic scattering. Phys. Lett. B 753, 221–226 (2016).
Blunden, P. G., Melnitchouk, W. & Thomas, A. W. New formulation of γZ box corrections to the weak charge of the proton. Phys. Rev. Lett. 107, 081801 (2011).
Blunden, P. G., Melnitchouk, W. & Thomas, A. W. γZ box corrections to weak charges of heavy nuclei in atomic parity violation. Phys. Rev. Lett. 109, 262301 (2012).
Gorchtein, M., Horowitz, C. J. & Ramsey-Musolf, M. J. Model dependence of the γZ dispersion correction to the parity-violating asymmetry in elastic ep scattering. Phys. Rev. C 84, 015502 (2011).
Wood, C. S. et al. Measurement of parity nonconservation and an anapole moment in cesium. Science 275, 1759–1763 (1997).
Dzuba, V. A., Berengut, J. C., Flambaum, V. V. & Roberts, B. Revisiting parity nonconservation in cesium. Phys. Rev. Lett. 109, 203003 (2012).
Green, J. et al. High-precision calculation of the strange nucleon electromagnetic form factors. Phys. Rev. D 92, 031501 (2015).
Sufian, R. S. et al. Strange quark magnetic moment of the nucleon at the physical point. Phys. Rev. Lett. 118, 042001 (2017).
Liu, J., McKeown, R. D. & Ramsey-Musolf, M. J. Global analysis of nucleon strange form factors at low Q 2. Phys. Rev. C 76, 025202 (2007).
Erler, J. & Ramsey-Musolf, M. J. Weak mixing angle at low energies. Phys. Rev. D 72, 073003 (2005).
Kumar, K. S., Mantry, S., Marciano, W. J. & Souder, P. A. Low-energy measurements of the weak mixing angle. Annu. Rev. Nucl. Part. Sci. 63, 237–267 (2013).
Seiberg, N. Naturalness versus supersymmetric non-renormalization theorems. Phys. Lett. B 318, 469–475 (1993).
Anthony, P. L. et al. Precision measurement of the weak mixing angle in Møller scattering. Phys. Rev. Lett. 95, 081601 (2005).
The Jefferson Lab PVDIS Collaboration. Measurement of parity violation in electron-quark scattering. Nature 506, 67–70 (2014).
The NuTeV Collaboration. Precise determination of electroweak parameters in neutrino–nucleon scattering. Phys. Rev. Lett. 88, 091802 (2002); errratum 90, 239902 (2003).
Bentz, W., Cloët, I. C., Londergan, J. T. & Thomas, A. W. Reassessment of the NuTeV determination of the weak mixing angle. Phys. Lett. B 693, 462–466 (2010).
Erler, J. & Su, S. The weak neutral current. Prog. Part. Nucl. Phys. 71, 119–149 (2013).
Davoudiasl, H., Lee, H.-S. & Marciano, W. J. Muon g−2, rare kaon decays, and parity violation from dark bosons. Phys. Rev. D 89, 095006 (2014).
Erler, J., Horowitz, C. J., Mantry, S. & Souder, P. A. Weak polarized electron scattering. Annu. Rev. Nucl. Part. Sci. 64, 269–298 (2014).
Eichten, E., Lane, K. D. & Peskin, M. E. New tests for quark and lepton substructure. Phys. Rev. Lett. 50, 811–814 (1983).
Abramowicz, H. et al. Search for first-generation leptoquarks at HERA. Phys. Rev. D 86, 012005 (2012).
Berger, N. et al. Measuring the weak mixing angle with the P2 experiment at MESA. J. China Univ. Sci. Tech. 46, 481–487 (2016).
Benesch, J. et al. The MOLLER experiment: an ultra-precise measurement of the weak mixing angle using Møller scattering. Preprint at https://arxiv.org/abs/1411.4088v2 (2014).
Musolf, M. J. et al. Intermediate-energy semileptonic probes of the hadronic neutral current. Phys. Rep. 239, 1–178 (1994).
Erler, J. & Ramsey-Musolf, M. J. Low energy tests of the weak interaction. Prog. Part. Nucl. Phys. 54, 351–442 (2005).
Armstrong, D. S. & McKeown, R. D. Parity-violating electron scattering and the electric and magnetic strange form factors of the proton. Annu. Rev. Nucl. Part. Sci. 62, 337–359 (2012).
G0 Collaboration. Strange quark contributions to parity-violating asymmetries in the forward G0 electron–proton scattering experiment. Phys. Rev. Lett. 95, 092001 (2005).
G0 Collaboration. Strange quark contributions to parity-violating asymmetries in the backward angle G0 electron scattering experiment. Phys. Rev. Lett. 104, 012001 (2010).
HAPPEX Collaboration. Parity-violating electroweak asymmetry in ep scattering. Phys. Rev. C 69, 065501 (2004).
HAPPEX Collaboration. Constraints on the nucleon strange form-factors at Q 2 ~ 0.1 GeV2. Phys. Lett. B 635, 275–279 (2006).
HAPPEX Collaboration. Precision measurements of the nucleon strange form factors at Q 2 ~ 0.1 GeV2. Phys. Rev. Lett. 98, 032301 (2007).
HAPPEX Collaboration. New precision limit on the strange vector form factors of the proton. Phys. Rev. Lett. 108, 102001 (2012).
Spayde, D. T. et al. The strange quark contribution to the proton’s magnetic moment. Phys. Lett. B 583, 79–86 (2004).
Maas, F. E. et al. Measurement of strange quark contributions to the nucleon’s form-factors at Q2 = 0.230 (GeV/c)2. Phys. Rev. Lett. 93, 022002 (2004).
Maas, F. E. et al. Evidence for strange quark contributions to the nucleon’s form-factors at Q 2 = 0.108 (GeV/c)2. Phys. Rev. Lett. 94, 152001 (2005).
Baunack, S. et al. Measurement of strange quark contributions to the vector form factors of the proton at Q 2 = 0.22 (GeV/c)2. Phys. Rev. Lett. 102, 151803 (2009).
HAPPEX Collaboration. Parity-violating electron scattering from 4He and the strange electric form factor of the nucleon. Phys. Rev. Lett. 96, 022003 (2006).
Balaguer Ríos, D. et al. Measurement of the parity violating asymmetry in the quasielastic electron-deuteron scattering and improved determination of the magnetic strange form factor and the isovector anapole radiative correction. Phys. Rev. D 94, 051101 (2016).
SAMPLE Collaboration. Parity violating electron deuteron scattering and the proton’s neutral weak axial vector form-factor. Phys. Rev. Lett. 92, 102003 (2004).
González-Jiménez, R., Caballero, J. A. & Donnelly, T. W. Global analysis of parity-violating asymmetry data for elastic electron scattering. Phys. Rev. D 90, 033002 (2014).
Zhu, S., Puglia, S. J., Holstein, B. R. & Ramsey-Musolf, M. J. Nucleon anapole moment and parity-violating ep scattering. Phys. Rev. D 62, 033008 (2000).
Kelly, J. J. Simple parametrization of nucleon form factors. Phys. Rev. C 70, 068202 (2004).
Galster, S., Klein, H., Moritz, J., Schmidt, K. H. & Wegener, D. Elastic electron–deuteron scattering and the electric neutron form factor at four momentum transfers 5 fm−2 < q 2 < 14 fm−2. Nucl. Phys. B 32, 221–237 (1971).
Venkat, S., Arrington, J., Miller, G. A. & Zhan, X. Realistic transverse images of the proton charge and magnetic densities. Phys. Rev. C 83, 015203 (2011).
Rislow, B. C. & Carlson, C. E. Modification of electromagnetic structure functions for the γZ -box diagram. Phys. Rev. D 88, 013018 (2013).
Grames, J. et al. Two Wien filter spin flipper. In Proc. 2011 Particle Accelerator Conference (eds Satogata, T. & Brown, K.) 862–864 (IEEE, New York, 2011).
Arrington, J., Blunden, P. G. & Melnitchouk, W. Review of two-photon exchange in electron scattering. Prog. Part. Nucl. Phys. 66, 782–833 (2011).
Qweak Collaboration. Beam normal single spin asymmetry measurements from Q weak. Preprint at https://arxiv.org/abs/1604.04602 (2016).
Kargiantoulakis, E. A Precision Test of the Standard Model via Parity-Violating Electron Scattering in the Q weak Experiment. PhD thesis, Univ. Virginia (2015); https://misportal.jlab.org/ul/publications/view_pub.cfm?pub_id=14261.
Agostinelli, S. et al. Geant4 – a simulation toolkit. Nucl. Instrum. Meth. A 506, 250–303 (2003).
Abrahamyan, S. et al. New measurements of the transverse beam asymmetry for elastic electron scattering from selected nuclei. Phys. Rev. Lett. 109, 192501 (2012).
Gorchtein, M. & Horowitz, C. J. Analyzing power in elastic scattering of the electrons off a spin-0 target. Phys. Rev. C 77, 044606 (2008).
Hauger, M. et al. A high-precision polarimeter. Nucl. Instrum. Meth. A 462, 382–392 (2001).
Magee, J. et al. A novel comparison of Møller and Compton electron-beam polarimeters. Phys. Lett. B 766, 339–344 (2017).
Horowitz, C. J. Parity violating elastic electron scattering from 27Al and the QWEAK measurement. Phys. Rev. C 89, 045503 (2014).
McHugh, M. A Measurement of the Transverse Asymmetry in Forward-Angle Electron-Carbon Scattering Using the Q weak Apparatus. PhD thesis, George Washington Univ. (2017); https://misportal.jlab.org/ul/publications/view_pub.cfm?pub_id=14918.
Ferroglia, A., Ossola, G. & Sirlin, A. Bounds on M W, M t, \({\sin }^{2}{\theta }_{{\rm{e}}{\rm{f}}{\rm{f}}}^{{\rm{l}}{\rm{e}}{\rm{p}}{\rm{t}}}\). Eur. Phys. J. C 35, 501–507 (2004).
Bethke, S. αs 2002. Nucl. Phys. B Proc. Sup. 121, 74–81 (2003).
Acknowledgements
This work was supported by the US Department of Energy (DOE) Contract number DEAC05-06OR23177, under which Jefferson Science Associates, LLC, operates the Thomas Jefferson National Accelerator Facility. Construction and operating funding for the experiment was provided through the US DOE, the Natural Sciences and Engineering Research Council of Canada (NSERC), the Canadian Foundation for Innovation (CFI), and the National Science Foundation (NSF) with university matching contributions from the College of William and Mary, Virginia Tech, George Washington University and Louisiana Tech University. We thank the staff of Jefferson Laboratory, in particular the accelerator operations staff, the target and cryogenic groups, the radiation control staff, as well as the Hall C technical staff for their help and support. We are grateful for the contributions of our undergraduate students. We thank TRIUMF for its contributions to the development of the spectrometer and integrated electronics, and BATES for its contributions to the spectrometer and Compton polarimeter. We are indebted to P. G. Blunden, J. D. Bowman, J. Erler, N. L. Hall, W. Melnitchouk, M. J. Ramsey-Musolf and A. W. Thomas for discussions. We also thank P. A. Souder for contributions to the analysis. Figure 2 was adapted with permission from ref. 3 (copyrighted by the American Physical Society).
Author information
Authors and Affiliations
Consortia
Contributions
Authors contributed to one or more of the following areas: proposing, leading and running the experiment; design, construction, optimization and testing of the experimental apparatus and data acquisition system; data analysis; simulation; extraction of the physics results from measured asymmetries; and the writing of this Letter.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Fig. 1 Apparatus.
a, Schematic of critical accelerator components and the Qweak apparatus4. The electron beam is generated at the photocathode, accelerated by the Continuous Electron Beam Accelerator Facility (CEBAF) and sent to experimental Hall C, where it is monitored by beam position monitors and beam current monitors. The insertable half-wave plate (IHWP) provides slow reversal of the electron beam helicity. The data acquisition system records the data. b, Computer-aided design drawing of the experimental apparatus. c, The Qweak apparatus, before the final shielding configuration was installed. d, Interior of the hut shielding the detectors, showing two of the Cherenkov detectors (right) and a pair of tracking chambers (left).
Extended Data Fig. 2 Beamline background.
Determination of Abb, the false asymmetry arising from beamline background events. Uncertainties are 1 s.d. a, Correlation of the main detector asymmetry to that of the upstream luminosity monitors, measured when the signal from elastically scattered electrons in the main detectors was blocked at the first collimator. b, Correlation of asymmetries from the upstream luminosity monitors with one of the other background detectors (a bare PMT located in the detector shield house). c, Correlation of the unblocked main detector asymmetry to that of the upstream luminosity monitor for Run 2. Our Abb determination was based on this slope.
Extended Data Fig. 3 Rescattering bias.
a, Schematic illustrating the precession of longitudinally polarized electrons through the spectrometer magnet, generating sizeable transverse spin components upon arrival at the detector array (spin directions indicated by red and blue arrows for the two electron helicity states). An end-view of the detector array, indicating the right (R) and left (L) PMT positions, is shown on the left. b, Difference between the asymmetry measured by the two (R and L) PMT tubes versus the detector number (Run 2 data). c, Calculated rescattering bias Abias versus detector number, with the eight-detector-averaged value shown by the red lines. Uncertainties (1 s.d.) are systematic.
Extended Data Fig. 4 Electron beam polarization.
Measurements from the Compton (closed blue circles) and Møller (open red squares) polarimeters during Run 2. Inner error bars denote statistical uncertainties and outer error bars show the statistical and point-to-point systematic uncertainties added in quadrature. Normalization, or scale-type, uncertainties are shown by the solid blue (Compton) and red (Møller) bands. All uncertainties are 1 s.d. The yellow band shows the derived polarization values used in the evaluation of the parity-violating asymmetry Aep. The time dependence of the reported polarization is driven primarily by the continuous Compton measurements, with a small-scale correction (0.21%, not included in this figure) determined from an uncertainty-weighted global comparison of the Compton and Møller polarimeters.
Extended Data Fig. 5 Asymmetry from aluminium.
Parity-violating asymmetry from the aluminium alloy target versus the dataset number. All uncertainties are 1 s.d. The labels ‘IN’ and ‘OUT’ refer to the state of the insertable half-wave plate at the electron source, which generated a 180° flip of the electron spin when IN. The subscripts denote the setting of the Wien filter, with L and R corresponding to the presence and absence, respectively, of an additional 180° rotation of the spin direction of the electron beam. A period in which a further 180° flip was generated through (ge − 2) precession (ge, electron gyromagnetic ratio) via a modified accelerator configuration during Wien 6 is indicated. The combinations OUT–R and IN–L with no (ge − 2) spin flip reveal the physical sign of the asymmetry. Solid lines represent the time-averaged values, and the horizontal dashed line indicates zero asymmetry. The vertical dashed lines delineate particular data subsets with a given Wien filter setting.
Extended Data Fig. 6 Asymmetry from the proton.
Observed parity-violating asymmetry Aep after all corrections, versus the dataset number (acquired in the double-Wien-filter configuration). The Wien filter reversed the beam helicity at approximately monthly intervals. The subscripts denote the setting of the Wien filter as L or R, corresponding to the presence or absence, respectively, of a 180° rotation of the spin direction of the electron beam. IN and OUT refer to the state of the insertable half-wave plate at the electron source, generating an additional 180° flip of the spin when IN. A period in which a further 180° flip was generated through (ge − 2) precession via a modified accelerator configuration is indicated. The combinations OUT–R and IN–L with no (ge − 2) flip reveal the physical sign of the asymmetry. Solid lines represent the time-averaged values and the dashed line indicates zero asymmetry. The uncertainties (1 s.d.) shown are those of the corresponding Amsr values (see text) only—that is, they do not include time-independent uncertainties—so as to illustrate the time stability of the results. The weighted mean and P-value of the upper OUT–L and IN–R data are 226.9 ± 10.2, P = 0.59 (upper solid line), respectively. For the opposite combination, OUT–R and IN–L, we find a weighted mean of −226.1 ± 10.5 and P = 0.36 (lower solid line).
Rights and permissions
About this article
Cite this article
The Jefferson Lab Qweak Collaboration. Precision measurement of the weak charge of the proton. Nature 557, 207–211 (2018). https://doi.org/10.1038/s41586-018-0096-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0096-0
This article is cited by
-
Dark showers from Z-dark Z′ mixing
Journal of High Energy Physics (2024)
-
Leading directions in the SMEFT
Journal of High Energy Physics (2023)
-
Asymmetric leptoquark pair production at LHC
Journal of High Energy Physics (2023)
-
Physics implications of a combined analysis of COHERENT CsI and LAr data
Journal of High Energy Physics (2023)
-
Global fit of modified quark couplings to EW gauge bosons and vector-like quarks in light of the Cabibbo angle anomaly
Journal of High Energy Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.