Abstract
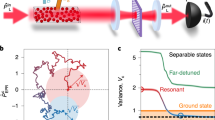
Quantum entanglement is a phenomenon whereby systems cannot be described independently of each other, even though they may be separated by an arbitrarily large distance1. Entanglement has a solid theoretical and experimental foundation and is the key resource behind many emerging quantum technologies, including quantum computation, cryptography and metrology. Entanglement has been demonstrated for microscopic-scale systems, such as those involving photons2,3,4,5, ions6 and electron spins7, and more recently in microwave and electromechanical devices8,9,10. For macroscopic-scale objects8,9,10,11,12,13,14, however, it is very vulnerable to environmental disturbances, and the creation and verification of entanglement of the centre-of-mass motion of macroscopic-scale objects remains an outstanding goal. Here we report such an experimental demonstration, with the moving bodies being two massive micromechanical oscillators, each composed of about 1012 atoms, coupled to a microwave-frequency electromagnetic cavity that is used to create and stabilize the entanglement of their centre-of-mass motion15,16,17. We infer the existence of entanglement in the steady state by combining measurements of correlated mechanical fluctuations with an analysis of the microwaves emitted from the cavity. Our work qualitatively extends the range of entangled physical systems and has implications for quantum information processing, precision measurements and tests of the limits of quantum mechanics.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
05 November 2018
Coding errors in some of the equations in the online version of this article were fixed on Monday 5 November 2018.
References
Einstein, A., Podolsky, B. & Rosen, N. Can quantum-mechanical description of physical reality be considered complete? Phys. Rev. 47, 777–780 (1935).
Aspect, A., Dalibard, J. & Roger, G. Experimental test of Bell’s inequalities using time-varying analyzers. Phys. Rev. Lett. 49, 1804–1807 (1982).
Heidmann, A. et al. Observation of quantum noise reduction on twin laser beams. Phys. Rev. Lett. 59, 2555–2557 (1987).
Ou, Z. Y., Pereira, S. F., Kimble, H. J. & Peng, K. C. Realization of the Einstein–Podolsky–Rosen paradox for continuous variables. Phys. Rev. Lett. 68, 3663–3666 (1992).
Bowen, W. P., Treps, N., Schnabel, R. & Lam, P. K. Experimental demonstration of continuous variable polarization entanglement. Phys. Rev. Lett. 89, 253601 (2002).
Jost, J. D. et al. Entangled mechanical oscillators. Nature 459, 683–685 (2009).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Steffen, M. et al. Measurement of the entanglement of two superconducting qubits via state tomography. Science 313, 1423–1425 (2006).
DiCarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010).
Palomaki, T. A., Teufel, J. D., Simmonds, R. W. & Lehnert, K. W. Entangling mechanical motion with microwave fields. Science 342, 710–713 (2013).
Leggett, A. J. Macroscopic quantum systems and the quantum theory of measurement. Prog. Theor. Phys. Suppl. 69, 80–100 (1980).
Julsgaard, B., Kozhekin, A. & Polzik, E. S. Experimental long-lived entanglement of two macroscopic objects. Nature 413, 400–403 (2001).
Lee, K. C. et al. Entangling macroscopic diamonds at room temperature. Science 334, 1253–1256 (2011).
Klimov, P. V., Falk, A. L., Christle, D. J., Dobrovitski, V. V. & Awschalom, D. D. Quantum entanglement at ambient conditions in a macroscopic solid-state spin ensemble. Sci. Adv. 1, e1501015 (2015).
Woolley, M. J. & Clerk, A. A. Two-mode squeezed states in cavity optomechanics via engineering of a single reservoir. Phys. Rev. A 89, 063805 (2014).
Woolley, M. J. & Clerk, A. A. Two-mode back-action-evading measurements in cavity optomechanics. Phys. Rev. A 87, 063846 (2013).
Ockeloen-Korppi, C. F. et al. Quantum backaction evading measurement of collective mechanical modes. Phys. Rev. Lett. 117, 140401 (2016).
Mancini, S., Giovannetti, V., Vitali, D. & Tombesi, P. Entangling macroscopic oscillators exploiting radiation pressure. Phys. Rev. Lett. 88, 120401 (2002).
Pinard, M. et al. Entangling movable mirrors in a double-cavity system. Europhys. Lett. 72, 747–753 (2005).
Tan, H., Li, G. & Meystre, P. Dissipation-driven two-mode mechanical squeezed states in optomechanical systems. Phys. Rev. A 87, 033829 (2013).
Wang, Y.-D. & Clerk, A. A. Reservoir-engineered entanglement in optomechanical systems. Phys. Rev. Lett. 110, 253601 (2013).
Li, J., Haghighi, I. M., Malossi, N., Zippilli, S. & Vitali, D. Generation and detection of large and robust entanglement between two different mechanical resonators in cavity optomechanics. New J. Phys. 17, 103037 (2015).
Mahboob, I., Okamoto, H., Onomitsu, K. & Yamaguchi, H. Two-mode thermal-noise squeezing in an electromechanical resonator. Phys. Rev. Lett. 113, 167203 (2014).
Pontin, A. et al. Dynamical two-mode squeezing of thermal fluctuations in a cavity optomechanical system. Phys. Rev. Lett. 116, 103601 (2016).
Wollman, E. E. et al. Quantum squeezing of motion in a mechanical resonator. Science 349, 952–955 (2015).
Pirkkalainen, J.-M., Damskägg, E., Brandt, M., Massel, F. & Sillanpää, M. A. Squeezing of quantum noise of motion in a micromechanical resonator. Phys. Rev. Lett. 115, 243601 (2015).
Lecocq, F., Clark, J. B., Simmonds, R. W., Aumentado, J. & Teufel, J. D. Quantum nondemolition measurement of a nonclassical state of a massive object. Phys. Rev. X 5, 041037 (2015).
Duan, L.-M., Giedke, G., Cirac, J. I. & Zoller, P. Inseparability criterion for continuous variable systems. Phys. Rev. Lett. 84, 2722–2725 (2000).
Banaszek, K. & Wódkiewicz, K. Nonlocality of the Einstein–Podolsky–Rosen state in the Wigner representation. Phys. Rev. A 58, 4345–4347 (1998).
Weedbrook, C. et al. Gaussian quantum information. Rev. Mod. Phys. 84, 621–669 (2012).
Teufel, J. D. et al. Sideband cooling of micromechanical motion to the quantum ground state. Nature 475, 359–363 (2011).
Acknowledgements
We thank S. Paraoanu and I. Petersen for discussions. This work was supported by the Academy of Finland (contracts 250280, 308290 and 307757) and by the European Research Council (615755-CAVITYQPD). We acknowledge funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement number 732894 (FETPRO HOT). For this work, we used the facilities of the Micronova Nanofabrication Center and the Low Temperature Laboratory.
Author information
Authors and Affiliations
Contributions
M.A.S. initiated the project and was involved in all subsequent stages. C.F.O.-K. carried out the measurements. C.F.O.-K. and E.D. analysed the data. E.D. and J.-M.P. designed and fabricated the devices. M.J.W., A.A.C., F.M. and M.A. developed the theory. All authors participated in the writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Supplementary Information
This file contains Supplementary Discussion, Supplementary Figures 1-10, Supplementary Tables 1-3, and additional references.
Rights and permissions
About this article
Cite this article
Ockeloen-Korppi, C.F., Damskägg, E., Pirkkalainen, JM. et al. Stabilized entanglement of massive mechanical oscillators. Nature 556, 478–482 (2018). https://doi.org/10.1038/s41586-018-0038-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41586-018-0038-x
Keywords
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.