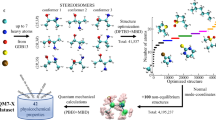
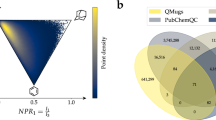
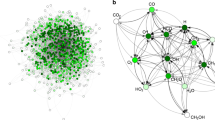
Abstract
Rational design of compounds with specific properties requires understanding and fast evaluation of molecular properties throughout chemical compound space — the huge set of all potentially stable molecules. Recent advances in combining quantum-mechanical calculations with machine learning provide powerful tools for exploring wide swathes of chemical compound space. We present our perspective on this exciting and quickly developing field by discussing key advances in the development and applications of quantum-mechanics-based machine-learning methods to diverse compounds and properties, and outlining the challenges ahead. We argue that significant progress in the exploration and understanding of chemical compound space can be made through a systematic combination of rigorous physical theories, comprehensive synthetic data sets of microscopic and macroscopic properties, and modern machine-learning methods that account for physical and chemical knowledge.

This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 digital issues and online access to articles
$119.00 per year
only $9.92 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Kirkpatrick, P. & Ellis, C. Chemical space. Nature 432, 823 (2004).
Mullard, A. The drug-maker’s guide to the galaxy. Nat. News 549, 445 (2017).
Huang, B. & von Lilienfeld, O. A. Efficient accurate scalable and transferable quantum machine learning with am-ons. Preprint at arXiv https://arxiv.org/abs/1707.04146 (2017).
Oprea T. I. et al. in Molecular Interaction Fields (Wiley-VCH, 2006).
Butina, D., Segall, M. D. & Frankcombe, K. Predicting ADME properties in silico: methods and models. Drug Discov. Today 7, S83–S88 (2002).
Rajan, K. Materials informatics. Mater. Today 8, 38–45 (2005).
Hautier, G., Fischer, C. C., Jain, A., Mueller, T. & Ceder, G. Finding nature’s missing ternary oxide compounds using machine learning and density functional theory. Chem. Mater. 22, 3762–3767 (2010).
Ward, L. & Wolverton, C. Atomistic calculations and materials informatics: a review. Curr. Opin. Solid State Mater. Sci. 21, 167–176 (2017).
Schneider, G. Virtual screening: an endless staircase? Nat. Rev. Drug Discov. 9, 273–276 (2010).
von Lilienfeld, O. A. First principles view on chemical compound space: gaining rigorous atomistic control of molecular properties. Int. J. Quantum Chem. 113, 1676–1689 (2013).
Van Noorden, R., Maher, B. & Nuzzo, R. The top 100 papers. Nat. News 514, 550–553 (2014).
Franceschetti, A. & Zunger, A. The inverse band-structure problem of finding an atomic configuration with given electronic properties. Nature 402, 60–63 (1999).
Jóhannesson, G. H. et al. Combined electronic structure and evolutionary search approach to materials design. Phys. Rev. Lett. 88, 255506 (2002).
Curtarolo, S. et al. The high-throughput highway to computational materials design. Nat. Mater. 12, 191–201 (2013).
Hafner, J., Wolverton, C. & Ceder, G. Toward computational materials design: the impact of density functional theory on materials research. MRS Bull. 31, 659–668 (2006).
Hachmann, J. et al. The Harvard clean energy project: large-scale computational screening and design of organic photovoltaics on the world community grid. J. Phys. Chem. Lett. 2, 2241–2251 (2011).
Marzari, N. Materials modelling: the frontiers and the challenges. Nat. Mater. 15, 381–382 (2016).
Alberi, K. et al. The 2019 materials by design roadmap. J. Phys. D Appl. Phys. 52, 013001 (2018).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Schmidhuber, J. Deep learning in neural networks: an overview. Neural Netw. 61, 85–117 (2015).
Capper, D. et al. DNA methylation-based classification of central nervous system tumours. Nature 555, 469–474 (2018).
Klauschen, F. et al. Scoring of tumor-infiltrating lymphocytes: from visual estimation to machine learning. Semin. Cancer Biol. 52, 151–157 (2018).
Jurmeister, P. et al. Machine learning analysis of DNA methylation profiles distinguishes primary lung squamous cell carcinomas from head and neck metastases. Sci. Transl Med. 11, eaaw8513 (2019).
Baldi, P., Sadowski, P. & Whiteson, D. Searching for exotic particles in high-energy physics with deep learning. Nat. Commun. 5, 4308 (2014).
Lengauer, T., Sander, O., Sierra, S., Thielen, A. & Kaiser, R. Bioinformatics prediction of HIV coreceptor usage. Nat. Biotechnol. 25, 1407–1410 (2007).
Blankertz, B., Tomioka, R., Lemm, S., Kawanabe, M. & Muller, K.-R. Optimizing spatial filters for robust EEG single-trial analysis. IEEE Signal. Process. Mag. 25, 41–56 (2008).
Perozzi, B., Al-Rfou, R. & Skiena, S. in Proc. ACM SIGKDD Int. Conf. Knowledge Discov. Data Mining, 701–710 (ACM, 2014).
Thrun, S. Burgard, W. & Fox, D. Probabilistic Robotics (MIT Press, 2005).
Lewis, M. M. Moneyball: The Art of Winning an Unfair Game (Norton, W. W., 2003).
Ferrucci, D., Levas, A., Bagchi, S., Gondek, D. & Mueller, E. T. Watson: beyond jeopardy! Artif. Intell. 199, 93–105 (2013).
Silver, D. et al. Mastering the game of Go with deep neural networks and tree search. Nature 529, 484–489 (2016).
Lejaeghere, K. et al. Reproducibility in density functional theory calculations of solids. Science 351, aad3000 (2016).
Rupp, M., von Lilienfeld, O. A. & Burke, K. Guest editorial: special topic on data-enabled theoretical chemistry. J. Chem. Phys. 148, 241401 (2018).
Schneider, W. F. & Guo, H. Machine learning. J. Phys. Chem. A 122, 879–879 (2018).
von Lilienfeld, O. A. Quantum machine learning in chemical compound space. Angew. Chem. Int. Ed. 57, 4164–4169 (2018).
Freeze, J. G., Kelly, H. R. & Batista, V. S. Search for catalysts by inverse design: artificial intelligence, mountain climbers, and alchemists. Chem. Rev. 119, 6595–6612 (2019).
Ramakrishnan, R. et al. Big data meets quantum chemistry approximations: the Δ-machine learning approach. J. Chem. Theory Comput. 11, 2087–2096 (2015).
Mardt, A., Pasquali, L., Wu, H. & Noé, F. VAMPnets for deep learning of molecular kinetics. Nat. Commun. 9, 5 (2018).
Rupp, M., Tkatchenko, A., Müller, K.-R. & von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Cortes, C., Jackel, L. D., Solla, S. A., Vapnik, V. & Denker, J. S. in Advances in Neural Information Processing Systems. 327–334 (1994).
Noé, F. Machine learning for molecular dynamics on long timescales. Preprint at arXiv https://arxiv.org/abs/1812.07669 (2018).
Noé, F., Olsson, S., Köhler, J. & Wu, H. Boltzmann generators: sampling equilibrium states of many-body systems with deep learning. Science 365, eaaw1147 (2019).
Fink, T., Bruggesser, H. & Reymond, J.-L. Virtual exploration of the small-molecule chemical universe below 160 daltons. Angew. Chem. Int. Ed. 44, 1504–1508 (2005).
Fink, T. & Reymond, J.-L. Virtual exploration of the chemical universe up to 11 atoms of C, N, O, F: assembly of 26.4 million structures (110.9 million stereoisomers) and analysis for new ring systems, stereochemistry, physicochemical properties, compound classes, and drug discovery. J. Chem. Inf. Model. 47, 342–353 (2007).
Blum, L. C. & Reymond, J.-L. 970 million druglike small molecules for virtual screening in the chemical universe database GDB-13. J. Am. Chem. Soc. 131, 8732–8733 (2009).
Ruddigkeit, L., van Deursen, R., Blum, L. & Reymond, J.-L. Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17. J. Chem. Inf. Model. 52, 2684–2875 (2012).
Montavon, G. et al. Machine learning of molecular electronic properties in chemical compound space. New J. Phys. 15, 095003 (2013).
Ramakrishnan, R., Dral, P. O., Rupp, M. & von Lilienfeld, O. A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data 1, 140022 (2014).
Chmiela, S. et al. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 3, e1603015 (2017).
Smith, J. S., Isayev, O. & Roitberg, A. E. ANI-1, A data set of 20 million calculated off-equilibrium conformations for organic molecules. Sci. Data 4, 170193 (2017).
Ong, S. et al. The materials project. Materials Project http://materialsproject.org/ (2011).
Saal, J. E., Kirklin, S., Aykol, M., Meredig, B. & Wolverton, C. Materials design and discovery with high-throughput density functional theory: the open quantum materials database (OQMD). JOM 65, 1501–1509 (2013).
Faber, F. A., Lindmaa, A., von Lilienfeld, O. A. & Armiento, R. Machine learning energies of 2 million elpasolite (ABC 2D 6) crystals. Phys. Rev. Lett. 117, 135502 (2016).
Bartók, A., Kermode, J., Bernstein, N. & Csányi, G. Machine learning a general-purpose interatomic potential for silicon. Phys. Rev. X. 8, 041048 (2018).
Pettifor, D. G. The structures of binary compounds. I. Phenomenological structure maps. J. Phys. C. Solid State Phys. 19, 285–313 (1986).
Pettifor, D. G. Structure maps for pseudobinary and ternary phases. Mater. Sci. Technol. 4, 675–691 (1988).
Willatt, M. J., Musil, F. & Ceriotti, M. Feature optimization for atomistic machine learning yields a data-driven construction of the periodic table of the elements. Phys. Chem. Chem. Phys. 20, 29661–29668 (2018).
Faber, F. A., Christensen, A. S., Huang, B. & von Lilienfeld, O. A. Alchemical and structural distribution based representation for universal quantum machine learning. J. Chem. Phys. 148, 241717 (2018).
Schütt, K. T., Sauceda, H. E., Kindermans, P.-J., Tkatchenko, A. & Müller, K.-R. SchNet–A deep learning architecture for molecules and materials. J. Chem. Phys. 148, 241722 (2018).
Bartók, A. et al. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 3, e1701816 (2017).
Sumpter, B. G. & Noid, D. W. Potential energy surfaces for macromolecules. A neural network technique. Chem. Phys. Lett. 192, 455–462 (1992).
Ho, T. S. & Rabitz, H. A general method for constructing multidimensional molecular potential energy surfaces from ab initio calculations. J. Chem. Phys. 104, 2584–2597 (1996).
Lorenz, S., Gross, A. & Scheffler, M. Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem. Phys. Lett. 395, 210–215 (2004).
Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
Bartók, A., Payne, M. C., Kondor, R. & Csányi, G. Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 145, 170901 (2016).
Hansen, K. et al. Assessment and validation of machine learning methods for predicting molecular atomization energies. J. Chem. Theory Comput. 9, 3404–3419 (2013).
Ramakrishnan, R. & von Lilienfeld, O. A. Many molecular properties from one kernel in chemical space. CHIMIA 69, 182–186 (2015).
Pilania, G., Wang, C., Jiang, X., Rajasekaran, S. & Ramprasad, R. Accelerating materials property predictions using machine learning. Sci. Rep. 3, 2810 (2013).
Schütt, K. et al. How to represent crystal structures for machine learning: Towards fast prediction of electronic properties. Phys. Rev. B 89, 205118 (2014).
Meredig, B. et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B 89, 094104 (2014).
Ward, L. et al. Including crystal structure attributes in machine learning models of formation energies via Voronoi tessellations. Phys. Rev. B 96, 024104 (2017).
Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).
Pyzer-Knapp, E. O., Li, K. & Aspuru-Guzik, A. Learning from the Harvard clean energy project: The use of neural networks to accelerate materials discovery. Adv. Funct. Mater. 25, 6495–6502 (2015).
Jørgensen, M. S., Larsen, U. F., Jacobsen, K. W. & Hammer, B. Exploration versus exploitation in global atomistic structure optimization. J. Phys. Chem. A 122, 1504–1509 (2018).
Chmiela, S., Sauceda, H. E., Poltavsky, I., Müller, K.-R. & Tkatchenko, A. sGDML: Constructing accurate and data efficient molecular force fields using machine learning. Comput. Phys. Commun. 240, 38–45 (2019).
Huang, B. & von Lilienfeld, O. A. Communication: Understanding molecular representations in machine learning: The role of uniqueness and target similarity. J. Chem. Phys. 145, 161102 (2016).
Pronobis, W., Tkatchenko, A. & Müller, K.-R. Many-body descriptors for predicting molecular properties with machine learning: Analysis of pairwise and three-body interactions in molecules. J. Chem. Theory Comput. 14, 2991–3003 (2018).
Braun, M. L., Buhmann, J. M. & Müller, K. R. On relevant dimensions in kernel feature spaces. J. Mach. Learn. Res. 9, 1875–1906 (2008).
von Lilienfeld, O. A., Ramakrishnan, R., Rupp, M. & Knoll, A. Fourier series of atomic radial distribution functions: A molecular fingerprint for machine learning models of quantum chemical properties. Int. J. Quantum Chem. 115, 1084–1093 (2015).
Christensen, A. S., Faber, F. A. & von Lilienfeld, O. A. Operators in quantum machine learning: response properties in chemical space. J. Chem. Phys. 150, 064105 (2019).
Bartók, A., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
Hansen, K., Biegler, F., von Lilienfeld, O. A., Müller, K.-R. & Tkatchenko, A. Machine learning predictions of molecular properties: Accurate many-body potentials and nonlocality in chemical space. J. Phys. Chem. Lett. 6, 2326–2331 (2015).
Faber, F., Lindmaa, A., von Lilienfeld, O. A. & Armiento, R. Crystal structure representations for machine learning models of formation energies. Int. J. Quantum Chem. 115, 1094–1101 (2015).
Huo, H. & Rupp, M. Unified representation for machine learning of molecules and crystals. Preprint at arXiv https://arxiv.org/abs/1704.06439 (2017).
Schütt, K. T., Arbabzadah, F., Chmiela, S., Müller, K. R. & Tkatchenko, A. Quantum-chemical insights from deep tensor neural networks. Nat. Commun. 8, 13890 (2017).
Unke, O. T. & Meuwly, M. A reactive, scalable, and transferable model for molecular energies from a neural network approach based on local information. J. Chem. Phys. 148, 241708 (2018).
Zubatyuk, R., Smith, J. S., Leszczynski, J. & Isayev, O. Accurate and transferable multitask prediction of chemical properties with an atoms-in-molecules neural network. Sci. Adv. 5, eaav6490 (2019).
Snyder, J. C., Rupp, M., Hansen, K., Müller, K.-R. & Burke, K. Finding density functionals with machine learning. Phys. Rev. Lett. 108, 253002 (2012).
Carleo, G. & Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 355, 602–606 (2017).
Brockherde, F., Li, L., Tuckerman, M. E., Burke, K. & Müller, K.-R. Bypassing the Kohn–Sham equations with machine learning. Nat. Commun. 8, 872 (2017).
Schütt, K., Gastegger, M., Tkatchenko, A., Müller, K.-R. & Maurer, R. Unifying machine learning and quantum chemistry with a deep neural network for molecular wavefunctions. Nat. Commun. 10, 5024 (2019).
Fabrizio, A., Grisafi, A., Meyer, B., Ceriotti, M. & Corminboeuf, C. Electron density learning of non-covalent systems. Chem. Sci. 10, 9424–9432 (2019).
Hermann, J., Schätzle, Z. & Noé, F. Deep neural network solution of the electronic Schrödinger equation. Preprint at arXiv https://arxiv.org/abs/1909.08423 (2019).
Pfau, D., Spencer, J. S. de A., Matthews, G. G. & Foulkes, W. M. C. Ab-initio solution of the many-electron Schrödinger equation with deep neural networks. Preprint at arXiv https://arxiv.org/abs/1909.02487 (2019).
Behler, J. Constructing high-dimensional neural network potentials: A tutorial review. Int. J. Quantum Chem. 115, 1032–1050 (2015).
Shapeev, A. Moment tensor potentials: A class of systematically improvable interatomic potentials. Multiscale Model. Simul. 14, 1153–1173 (2016).
Sauceda, H. E., Chmiela, S., Poltavsky, I., Müller, K.-R. & Tkatchenko, A. Molecular force fields with gradient-domain machine learning: Construction and application to dynamics of small molecules with coupled cluster forces. J. Chem. Phys. 150, 114102 (2019).
Deringer, V. L. et al. Computational surface chemistry of tetrahedral amorphous carbon by combining machine learning and density functional theory. Chem. Mater. 30, 7438–7445 (2018).
Caro, M. A., Aarva, A., Deringer, V. L., Csányi, G. & Laurila, T. Reactivity of amorphous carbon surfaces: rationalizing the role of structural motifs in functionalization using machine learning. Chem. Mater. 30, 7446–7455 (2018).
Chmiela, S., Sauceda, H. E., Müller, K.-R. & Tkatchenko, A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 9, 3887 (2018).
Smith, J. S., Isayev, O. & Roitberg, A. E. ANI-1: An extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 8, 3192–3203 (2017).
Collins, C. R., Gordon, G. J., von Lilienfeld, O. A. & Yaron, D. J. Constant size descriptors for accurate machine learning models of molecular properties. J. Chem. Phys. 148, 241718 (2018).
Chen, X., Jørgensen, M. S., Li, J. & Hammer, B. Atomic energies from a convolutional neural network. J. Chem. Theory Comput. 14, 3933–3942 (2018).
Pilania, G., Gubernatis, J. E. & Lookman, T. Multi-fidelity machine learning models for accurate bandgap predictions of solids. Comput. Mater. Sci. 129, 156–163 (2017).
Zaspel, B., Huang, H., Harbrecht & von Lilienfeld, O. A. Boosting quantum machine learning models with a multilevel combination technique: Pople diagrams revisited. J. Chem. Theory Comput. 15, 1546–1559 (2018).
Batra, R., Pilania, G., Uberuaga, B. & Ramprasad, R. Multifidelity information fusion with machine learning: A case study of dopant formation energies in hafnia. ACS Appl. Mater. Interfaces 11, 24906–24918 (2019).
Rupp, M., Ramakrishnan, R. & von Lilienfeld, O. A. Machine learning for quantum mechanical properties of atoms in molecules. J. Phys. Chem. Lett. 6, 3309–3313 (2015).
Botu, V. & Ramprasad, R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 115, 1074–1083 (2015).
Jacobsen, T. L., Jørgensen, M. S. & Hammer, B. On-the-fly machine learning of atomic potential in density functional theory structure optimization. Phys. Rev. Lett. 120, 026102 (2018).
Christensen, A. S. et al. QML: a Python toolkit for quantum machine learning. GitHub https://github.com/qmlcode/qml (2017).
Schütt, K. et al. SchNetPack: a deep learning toolbox for atomistic systems. J. Chem. Theory Comput. 15, 448–455 (2018).
Alber, M. et al. iNNvestigate neural networks! J. Mach. Learn. Res. 20, 1–8 (2019).
Lapuschkin, S. et al. Unmasking Clever Hans predictors and assessing what machines really learn. Nat. Commun. 10, 1096 (2019).
Binder, A. et al. Towards computational fluorescence microscopy: Machine learning-based integrated prediction of morphological and molecular tumor profiles. Preprint at arXiv https://arxiv.org/abs/1805.11178 (2018).
Gómez-Bombarelli, R. et al. Automatic chemical design using a data-driven continuous representation of molecules. ACS Cent. Sci. 4, 268–276 (2018).
Zunger, A. Inverse design in search of materials with target functionalities. Nat. Rev. Chem. 2, 0121 (2018).
Kuhn, C. & Beratan, D. N. Inverse strategies for molecular design. J. Phys. Chem. 100, 10595–10599 (1996).
von Lilienfeld, O. A., Lins, R. & Rothlisberger, U. Variational particle number approach for rational compound design. Phys. Rev. Lett. 95, 153002 (2005).
Wang, M., Hu, X., Beratan, D. N. & Yang, W. Designing molecules by optimizing potentials. J. Am. Chem. Soc. 128, 3228–3232 (2006).
d’Avezac, M. & Zunger, A. Identifying the minimum-energy atomic configuration on a lattice: Lamarckian twist on Darwinian evolution. Phys. Rev. B 78, 064102 (2008).
Bach, S. et al. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS One 10, e0130140 (2015).
Ribeiro, M. T., Singh, S. & Guestrin, C. in Proc. 22nd ACM SIGKDD Int. Conf. Knowledge Discov. Data Mining 1135–1144 (ACM, 2016).
Montavon, G., Samek, W. & Müller, K.-R. Methods for interpreting and understanding deep neural networks. Digital Signal. Process. 73, 1–15 (2018).
Hirshfeld, F. L. Bonded-atom fragments for describing molecular charge densities. Theor. Chim. Acta. 44, 129–138 (1977).
Lee, A. A. et al. Ligand biological activity predicted by cleaning positive and negative chemical correlations. Proc. Natl Acad. Sci. USA 116, 3373–3378 (2019).
Hohm, U. Dipole polarizability and bond dissociation energy. J. Chem. Phys. 101, 6362–6364 (1994).
Hohm, U. Is there a minimum polarizability principle in chemical reactions? J. Phys. Chem. A. 104, 8418–8423 (2000).
Geerlings, P., De Proft, F. & Langenaeker, W. Conceptual density functional theory. Chem. Rev. 103, 1793–1874 (2003).
Deng, J. et al. in Proc. IEEE Conf. Comput. Vision Pattern Recogn. 248–255 (IEEE, 2009).
Rohrbach, M., Amin, S., Andriluka, M. & Schiele, B.in Proc. IEEE Conf. Comput. Vision Pattern Recogn. 1194–1201 (IEEE, 2012).
Schwaighofer, A., Schroeter, T., Mika, S. & Blanchard, G. How wrong can we get? A review of machine learning approaches and error bars. Comb. Chem. High Throughput Screen. 12, 453–468 (2009).
Smith, R. C. Uncertainty Quantification: Theory, Implementation, and Applications (SIAM, 2013).
Smith, J. S., Nebgen, B., Lubbers, N., Isayev, O. & Roitberg, A. E. Less is more: Sampling chemical space with active learning. J. Chem. Phys. 148, 241733 (2018).
Gubaev, K., Podryabinkin, E. V. & Shapeev, A. V. Machine learning of molecular properties: Locality and active learning. J. Chem. Phys. 148, 241727 (2018).
Sugiyama, M. & Kawanabe, M. Machine Learning in Non-Stationary Environments: Introduction to Covariate Shift Adaptation (MIT Press, 2012).
Faber, F. A. et al. Prediction errors of molecular machine learning models lower than hybrid DFT error. J. Chem. Theory Comput. 13, 5255–5264 (2017).
Ramakrishnan, R., Hartmann, M., Tapavicza, E. & von Lilienfeld, O. A. Electronic spectra from TDDFT and machine learning in chemical space. J. Chem. Phys. 143, 084111 (2015).
Pronobis, W., Schütt, K. T., Tkatchenko, A. & Müller, K.-R. Capturing intensive and extensive DFT/TDDFT molecular properties with machine learning. Eur. Phys. J. B 91, 178 (2018).
Grisafi, A. et al. Transferable machine-learning model of the electron density. ACS Cent. Sci. 5, 57–64 (2019).
Lawrence, S. & Giles, C. L. Accessibility of information on the web. Nature 400, 107 (1999).
Lawrence, S. & Giles, C. L. Searching the world wide web. Science 280, 98–100 (1998).
Ginzburg I. & Horn, D. in Advances in Neural Information Processing Systems (eds Jordan, M. I., LeCun, Y. & Solla, S. A.) 224–231 (MIT Press, 1994).
Bogojeski, M., Vogt-Maranto, L., Tuckerman, M. E., Mueller, K.-R. & Burke, K. Density functionals with quantum chemical accuracy: from machine learning to molecular dynamics. Preprint at ChemRxiv https://doi.org/10.26434/chemrxiv.8079917.v1 (2019).
Smith, J. S. et al. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 10, 2903 (2019).
Ulissi, Z. W., Singh, A. R., Tsai, C. & Nørskov, J. K. Automated discovery and construction of surface phase diagrams using machine learning. J. Phys. Chem. Lett. 19, 3931–3935 (2016).
Meyer, B., Sawatlon, B., Heinen, S., von Lilienfeld, O. A. & Corminboeuf, C. Machine learning meets volcano plots: computational discovery of cross-coupling catalysts. Chem. Sci. 9, 7069–7077 (2018).
Corey, E. J., Wipke, W. T., Cramer, R. D. & Howe, W. J. Computer-assisted synthetic analysis. facile man-machine communication of chemical structure by interactive computer graphics. J. Am. Chem. Soc. 94, 421–430 (1972).
Herges, R. & Hoock, C. Reaction planning: Computer-aided discovery of a novel elimination reaction. Science 255, 711–713 (1992).
Szymkuć, S. et al. Computer-assisted synthetic planning: The end of the beginning. Angew. Chem. Int. Ed. 55, 5904–5937 (2016).
Schwaller, T., Gaudin, D., Lanyi, C., Bekas & Laino, T. “Found in translation”: predicting outcomes of complex organic chemistry reactions using neural sequence-to-sequence models. Chem. Sci. 9, 6091–6098 (2018).
Segler, M. H. S., Preuss, M. & Waller, M. P. Planning chemical syntheses with deep neural networks and symbolic AI. Nature 555, 604–610 (2018).
Leach, A. R. Molecular Modelling: Principles and Applications (Addison-Wesley Longman, 1998).
Helgaker, T., Jørgensen, P. & Olsen, J. Molecular Electronic-Structure Theory (Wiley, 2000).
Tuckerman, M. E. Statistical Mechanics: Theory and Molecular Simulation (Oxford Univ. Press, 2010).
Pozun, Z. D. et al. Optimizing transition states via kernel-based machine learning. J. Chem. Phys. 136, 174101–174109 (2012).
Rappé, A. K., Casewit, C. J., Colwell, K. S., Goddard, W. A. III & Skid, W. M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 114, 10024–10035 (1992).
Stewart, J. J. P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 13, 1173–1213 (2007).
Stewart, J. J. P. Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 19, 1–32 (2013).
Aradi, B., Hourahine, B. & Frauenheim, T. DFTB+, a sparse matrix-based implementation of the DFTB method. J. Phys. Chem. A 111, 5678–5684 (2007).
Marienwald, H., Pronobis, W., Müller, K.-R. & Nakajima, S. Tight bound of incremental cover trees for dynamic diversification. Preprint at arXiv https://arxiv.org/abs/1806.06126 (2018).
Gilmer, J., Schoenholz, S. S., Riley, F., Vinyals, O. & Dahl, G. E. in Proc. Int. Conf. Mach. Learn. 1263–1272 (2017).
Nebgen, B. et al. Transferable dynamic molecular charge assignment using deep neural networks. J. Chem. Theory Comput. 14, 4687–4698 (2018).
Eickenberg, M., Exarchakis, G., Hirn, M., Mallat, S. & Thiry, L. Solid harmonic wavelet scattering for predictions of molecule properties. J. Chem. Phys. 148, 241732 (2018).
Faber, F. A., Christensen, A. S. & von Lilienfeld O. A. in Machine Learning meets Quantum Physics, Lecture Notes in Physics (eds Schütt, K. T. et al.) (Springer, 2020).
Behler, J. Atom-centered symmetry functions for constructing high-dimensional neural networks potentials. J. Chem. Phys. 134, 074106 (2011).
Acknowledgements
All authors thank F. A. Faber and J. Wagner for preparing the graphics in Fig. 1 and the cover image related to this article, respectively. O.A.v.L. acknowledges funding from the Swiss National Science foundation (nos. PP00P2_138932 and 407540_167186 NFP 75 Big Data) and from the European Research Council (ERC-CoG grant QML). This work was partly supported by the NCCR MARVEL, funded by the Swiss National Science Foundation. A.T. acknowledges financial support from the European Research Council (ERC-CoG grant BeStMo). K.-R.M. acknowledges partial financial support by the German Federal Ministry of Education and Research (BMBF) under grants 01IS14013A-E, 01GQ1115 and 01GQ0850; Deutsche Forschungsgesellschaft (DFG) under grant Math+, EXC 2046/1, project ID 390685689 and by the Institute for Information & Communication Technology Promotion (IITP) grant funded by the Korea government (nos. 2017-0-00451 and 2017-0-01779). Correspondence to O.A.v.L., K.-R.M. and A.T.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the preparation of this manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information
Nature Reviews Chemistry thanks F. Noé, G. Csanyi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Related links
Accurate neural-network engine for molecular energies (ANI) neural-network package: https://github.com/isayev/ASE_ANI
QM9 challenge: https://tinyurl.com/y2e589wj
Repository of data sets for quantum machine learning: http://quantum-machine.org
SchNetPack: https://github.com/atomistic-machine-learning/schnetpack
Symmetrized gradient-domain machine learning (sGDML): http://quantum-machine.org/gdml/#code
Rights and permissions
About this article
Cite this article
von Lilienfeld, O.A., Müller, KR. & Tkatchenko, A. Exploring chemical compound space with quantum-based machine learning. Nat Rev Chem 4, 347–358 (2020). https://doi.org/10.1038/s41570-020-0189-9
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41570-020-0189-9