Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

A highly correlated topological bubble phase of composite fermions

Nature Physics volume 19, pages 689–693 (2023)Cite this article

Subjects

Abstract

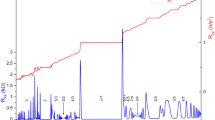
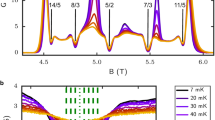
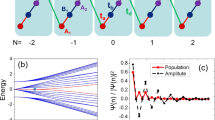
Strong interactions and topology drive a wide variety of correlated ground states. Some of the most interesting of these ground states, such as fractional quantum Hall states and fractional Chern insulators, have fractionally charged quasiparticles. Correlations in these phases are captured by the binding of electrons and vortices into emergent particles called composite fermions. Composite fermion quasiparticles are randomly localized at high levels of disorder and may exhibit charge order when there is not too much disorder in the system. However, more complex correlations are predicted when composite fermion quasiparticles cluster into a bubble, and then these bubbles order on a lattice. Such a highly correlated ground state is termed the bubble phase of composite fermions. Here we report the observation of such a bubble phase of composite fermions, evidenced by the re-entrance of the fractional quantum Hall effect. We associate this re-entrance with a bubble phase with two composite fermion quasiparticles per bubble. Our results demonstrate the existence of a new class of strongly correlated topological phases driven by clustering and charge ordering of emergent quasiparticles.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Representation of various topological phases of the electron gas with different bulk insulators.
Fig. 2: Magnetoresistance Rxx and Hall resistance Rxy over a broad range of magnetic fields B.
Fig. 3: Magnetoresistance Rxx and Hall resistance Rxy at selected values of the temperature.
Fig. 4: Magnetic field and temperature dependence of the magnetoresistance Rxx and Hall resistance Rxy for filling factors that include the ν = 5/3 to ν = 8/5 range.

Similar content being viewed by others

Data availability

Data are available upon request. Source data are provided with this paper.

References

  1. Klitzing, K. V., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).

    Article  ADS  Google Scholar 

  2. Zhitenev, N. B. et al. Imaging of localized electronic states in the quantum Hall regime. Nature 404, 473–476 (2000).

    Article  ADS  Google Scholar 

  3. Chen, Y. et al. Microwave resonance of the 2D Wigner crystal around integer Landau fillings. Phys. Rev. Lett. 91, 016801 (2003).

    Article  ADS  Google Scholar 

  4. Shayegan, M. Wigner crystals in flat band 2D electron systems. Nat. Rev. Phys. 4, 212–213 (2022).

    Article  Google Scholar 

  5. Tiemann, L., Rhone, T. D., Shibata, N. & Muraki, K. NMR profiling of quantum electron solids in high magnetic fields. Nat. Phys. 10, 648–652 (2014).

    Article  Google Scholar 

  6. Jang, J., Hunt, B. M., Pfeiffer, L. N., West, K. W. & Ashoori, R. C. Sharp tunnelling resonance from the vibrations of an electronic Wigner crystal. Nat. Phys. 13, 340–344 (2017).

    Article  Google Scholar 

  7. Liu, Y. et al. Observation of reentrant integer quantum Hall states in the lowest Landau level. Phys. Rev. Lett. 109, 036801 (2012).

    Article  ADS  Google Scholar 

  8. Myers, S. A., Huang, H., Pfeiffer, L. N., West, K. W. & Csáthy, G. A. Magnetotransport patterns of collective localization near ν = 1 in a high-mobility two-dimensional electron gas. Phys. Rev. B 104, 045311 (2021).

    Article  ADS  Google Scholar 

  9. Shingla, V., Myers, S. A., Pfeiffer, L. N., Baldwin, K. W. & Csáthy, G. A. Particle-hole symmetry and the reentrant integer quantum Hall Wigner solid. Commun. Phys. 4, 204 (2021).

    Article  Google Scholar 

  10. Zhou, H., Polshyn, H., Taniguchi, T., Watanabe, K. & Young, A. F. Solids of quantum Hall skyrmions in graphene. Nat. Phys. 16, 154–158 (2020).

    Article  Google Scholar 

  11. Koulakov, A. A., Fogler, M. M. & Shklovskii, B. I. Charge density wave in two-dimensional electron liquid in weak magnetic field. Phys. Rev. Lett. 76, 499–502 (1996).

    Article  ADS  Google Scholar 

  12. Moessner, R. & Chalker, J. T. Exact results for interacting electrons in high Landau levels. Phys. Rev. B 54, 5006–5015 (1996).

    Article  ADS  Google Scholar 

  13. Lilly, M. P., Cooper, K. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Evidence for an anisotropic state of two-dimensional electrons in high Landau levels. Phys. Rev. Lett. 82, 394–397 (1999).

    Article  ADS  Google Scholar 

  14. Du, R. R. et al. Strongly anisotropic transport in higher two-dimensional Landau levels. Solid State Commun. 109, 389–394 (1999).

    Article  ADS  Google Scholar 

  15. Cooper, K. B., Lilly, M. P., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Insulating phases of two-dimensional electrons in high Landau levels: observation of sharp thresholds to conduction. Phys. Rev. B 60, R11285 (1999).

    Article  ADS  Google Scholar 

  16. Eisenstein, J. P., Cooper, K. B., Pfeiffer, L. N. & West, K. W. Insulating and fractional quantum Hall states in the first excited Landau level. Phys. Rev. Lett. 88, 076801 (2002).

    Article  ADS  Google Scholar 

  17. Fu, X. et al. Two-and three-electron bubbles in AlxGa1−xAs/Al0.24Ga0.76As quantum wells. Phys. Rev. B 99, 161402 (2019).

    Article  ADS  Google Scholar 

  18. Ro, D. et al. Electron bubbles and the structure of the orbital wave function. Phys. Rev. B 99, 201111 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  19. Chen, S. et al. Competing fractional quantum Hall and electron solid phases in graphene. Phys. Rev. Lett. 122, 026802 (2019).

    Article  ADS  Google Scholar 

  20. Stormer, H. L., Tsui, D. C. & Gossard, A. C. The fractional quantum Hall effect. Rev. Mod. Phys. 71, S298–S305 (1999).

    Article  MathSciNet  Google Scholar 

  21. Du, X., Skachko, I., Duerr, F., Luican, A. & Andrei, E. Y. Fractional quantum Hall effect and insulating phase of Dirac electrons in graphene. Nature 462, 192–195 (2009).

    Article  ADS  Google Scholar 

  22. Bolotin, K. I., Ghahari, F., Shulman, M. D., Stormer, H. L. & Kim, P. Observation of the fractional quantum Hall effect in graphene. Nature 462, 196–199 (2009).

    Article  ADS  Google Scholar 

  23. Spanton, E. M. et al. Observation of fractional Chern insulators in a van der Waals heterostructure. Science 360, 62–66 (2018).

    Article  ADS  Google Scholar 

  24. Xie, Y. et al. Fractional Chern insulators in magic-angle twisted bilayer graphene. Nature 600, 439–443 (2021).

    Article  ADS  Google Scholar 

  25. Pierce, A. T. et al. Unconventional sequence of correlated Chern insulators in magic-angle twisted bilayer graphene. Nat. Phys. 17, 1210–1215 (2021).

    Article  Google Scholar 

  26. Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983).

    Article  ADS  Google Scholar 

  27. Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989).

    Article  ADS  Google Scholar 

  28. Martin, J. et al. Localization of fractionally charged quasi-particles. Science 305, 980–983 (2004).

    Article  ADS  Google Scholar 

  29. Yi, H. & Fertig, H. A. Laughlin-Jastrow-correlated Wigner crystal in a strong magnetic field. Phys. Rev. B 58, 4019–4027 (1998).

    Article  ADS  Google Scholar 

  30. Narevich, R., Murthy, G. & Fertig, H. A. Hamiltonian theory of the composite-fermion Wigner crystal. Phys. Rev. B 64, 245326 (2001).

    Article  ADS  Google Scholar 

  31. Chang, C. C., Jeon, G. S. & Jain, J. K. Microscopic verification of topological electron-vortex binding in the lowest Landau-level crystal state. Phys. Rev. Lett. 94, 016809 (2005).

    Article  ADS  Google Scholar 

  32. He, W. J. et al. Phase boundary between the fractional quantum Hall liquid and the Wigner crystal at low filling factors and low temperatures: a path integral Monte Carlo study. Phys. Rev. B 72, 195306 (2005).

    Article  ADS  Google Scholar 

  33. Chang, C. C., Töke, C., Jeon, G. S. & Jain, J. K. Competition between composite-fermion-crystal and liquid orders at ν = 1∕ 5. Phys. Rev. B 73, 155323 (2006).

    Article  ADS  Google Scholar 

  34. Archer, A. C., Park, K. & Jain, J. K. Competing crystal phases in the lowest Landau level. Phys. Rev. Lett. 111, 146804 (2013).

    Article  ADS  Google Scholar 

  35. Zhao, J., Zhang, Y. & Jain, J. K. Crystallization in the fractional quantum Hall regime induced by Landau-level mixing. Phys. Rev. Lett. 121, 116802 (2018).

    Article  ADS  Google Scholar 

  36. Zuo, Z. W. et al. Interplay between fractional quantum Hall liquid and crystal phases at low filling. Phys. Rev. B 102, 075307 (2020).

    Article  ADS  Google Scholar 

  37. Archer, A. C. & Jain, J. K. Static and dynamic properties of type-II composite fermion Wigner crystals. Phys. Rev. B 84, 115139 (2011).

    Article  ADS  Google Scholar 

  38. Zhu, H. et al. Observation of a pinning mode in a Wigner solid with ν = 1/3 fractional quantum Hall excitations. Phys. Rev. Lett. 105, 126803 (2010).

    Article  ADS  Google Scholar 

  39. Lee, S. Y., Scarola, V. W. & Jain, J. K. Structures for interacting composite fermions: stripes, bubbles, and fractional quantum Hall effect. Phys. Rev. B 66, 085336 (2002).

    Article  ADS  Google Scholar 

  40. Goerbig, M. O., Lederer, P. & Smith, C. M. Possible reentrance of the fractional quantum hall effect in the lowest Landau level. Phys. Rev. Lett. 93, 216802 (2004).

    Article  ADS  Google Scholar 

  41. Du, R. R. et al. Fractional quantum Hall effect around ν = 3/2: composite fermions with a spin. Phys. Rev. Lett. 75, 3926–3929 (1995).

    Article  ADS  Google Scholar 

  42. Liu, Y. et al. Spin polarization of composite fermions and particle-hole symmetry breaking. Phys. Rev. B 90, 085301 (2014).

    Article  ADS  Google Scholar 

  43. Eisenstein, J. P., Stormer, H. L., Pfeiffer, L. N. & West, K. W. Evidence for a phase transition in the fractional quantum Hall effect. Phys. Rev. Lett. 62, 1540–1543 (1989).

    Article  ADS  Google Scholar 

  44. Deng, N. et al. Collective nature of the reentrant integer quantum Hall states in the second Landau level. Phys. Rev. Lett. 108, 086803 (2012).

    Article  ADS  Google Scholar 

  45. Goerbig, M. O., Lederer, P. & Smith, C. M. Competition between quantum-liquid and electron-solid phases in intermediate Landau levels. Phys. Rev. B 69, 115327 (2004).

    Article  ADS  Google Scholar 

  46. Pan, W. et al. Fractional quantum Hall effect of composite fermions. Phys. Rev. Lett. 90, 016801 (2003).

    Article  ADS  Google Scholar 

  47. Samkharadze, N., Arnold, I., Pfeiffer, L. N., West, K. W. & Csáthy, G. A. Observation of incompressibility at ν = 4/11 and ν = 5/13. Phys. Rev. B 91, 081109(R) (2015).

    Article  ADS  Google Scholar 

  48. Schreiber, K. A. & Csáthy, G. A. Competition of pairing and nematicity in the two-dimensional electron gas. Annu. Rev. Condens. Matter Phys. 11, 17–35 (2020).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We acknowledge useful discussions with J. Jain and V. Scarola. Measurements at Purdue were supported by the NSF DMR Grant No. 1904497. The sample growth effort of L.N.P., K.W.W. and K.W.B. of Princeton University was supported by the Gordon and Betty Moore Foundation Grant No. GBMF 4420 and the National Science Foundation MRSEC Grant No. DMR-1420541.

Author information

Author notes

  1. These authors contributed equally: Vidhi Shingla, Haoyun Huang.

Authors and Affiliations

  1. Department of Physics and Astronomy, Purdue University, West Lafayette, IN, USA

    Vidhi Shingla, Haoyun Huang & Gábor A. Csáthy

  2. Department of Physics, Monmouth College, Monmouth, IL, USA

    Ashwani Kumar

  3. Department of Electrical Engineering, Princeton University, Princeton, NJ, USA

    Loren N. Pfeiffer, Kenneth W. West & Kirk W. Baldwin

Authors
  1. Vidhi Shingla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haoyun Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ashwani Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Loren N. Pfeiffer
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Kenneth W. West
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Kirk W. Baldwin
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Gábor A. Csáthy
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

V.S. and A.K. performed low-temperature transport measurements. L.N.P., K.W.W. and K.W.B. produced molecular beam epitaxy-grown GaAs/AlGaAs samples and characterized them. V.S., H.H. and G.A.C. analysed the data and wrote the paper.

Corresponding author

Correspondence to Gábor A. Csáthy.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Multiple observations of the RFQHS.

Several longitudinal magnetoresistance 𝑅𝑥𝑥 and Hall resistance 𝑅x𝑦 measurements. Panels a and b have data from Sample 1, collected after cycling the sample to room temperature. Panel c has data from Sample 2. All panels exhibit the RFQHS, as evident from a splitting of the longitudinal magnetoresistance into two peaks and reentrance of the Hall resistance to Rxy = 3h/5e2.

Source data

Extended Data Fig. 2 The longitudinal magnetoresistance Rxx and Ryy as measured along two mutually perpendicular crystal directions and the Hall resistance.

Data were collected from Sample 1 at T = 12 mK. While there are small but noticeable differences in the two longitudinal magnetoresistance traces, at the formation of the RFQHS the longitudinal magnetoresistance is nearly vanishing for both crystal directions and it is nearly isotropic. Panels a and b show data collected along two mutually perpendicular crystal axes of the GaAs crystal.

Source data

Supplementary information

Supplementary Information

Supplementary text and references.

Source data

Source Data Fig. 2

Raw data for Fig. 2 of the main text.

Source Data Fig. 3

Raw data for Fig. 3 of the main text.

Source Data Extended Data Fig. 1

Raw data for Extended Data Fig. 1 of the Supplementary Information.

Source Data Extended Data Fig. 2

Raw data for Extended Data Fig. 2 of the Supplementary Information.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shingla, V., Huang, H., Kumar, A. et al. A highly correlated topological bubble phase of composite fermions. Nat. Phys. 19, 689–693 (2023). https://doi.org/10.1038/s41567-023-01939-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-023-01939-2

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing