Observation of triple J/ψ meson production in proton-proton collisions

Abstract

Protons consist of three valence quarks, two up-quarks and one down-quark, held together by gluons and a sea of quark-antiquark pairs. Collectively, quarks and gluons are referred to as partons. In a proton-proton collision, typically only one parton of each proton undergoes a hard scattering – referred to as single-parton scattering – leaving the remainder of each proton only slightly disturbed. Here, we report the study of double- and triple-parton scatterings through the simultaneous production of three J/ψ mesons, which consist of a charm quark-antiquark pair, in proton-proton collisions recorded with the CMS experiment at the Large Hadron Collider. We observed this process – reconstructed through the decays of J/ψ mesons into pairs of oppositely charged muons – with a statistical significance above five standard deviations. We measured the inclusive fiducial cross-section to be $27{2}_{-104}^{+141}\,{{{\rm{(stat)}}}}\,\pm 17\,{{{\rm{(syst)}}}}\,{{{\rm{fb}}}}\,$, and compared it to theoretical expectations for triple-J/ψ meson production in single-, double- and triple-parton scattering scenarios. Assuming factorization of multiple hard-scattering probabilities in terms of single-parton scattering cross-sections, double- and triple-parton scattering are the dominant contributions for the measured process.

Main

High-energy particle accelerators are unique tools to study the structure of matter at the shortest distances. The most powerful accelerator today is the CERN Large Hadron Collider (LHC) that has so far collided beams of protons with energies of up to 6.5 TeV, resulting in centre-of-mass energies of up to 13 TeV. Protons are used in energy-frontier colliders because they are relatively easy to accelerate and keep in a circular orbit to enable high collision rates. However, they are not fundamental particles and, in fact, have a complicated quantum mechanical structure. Protons consist of three quarks, two up-type and one down-type, and gluons, which hold together the three valence quarks, as well as of a ‘sea’ of virtual quark–antiquark pairs, which are fundamental elements of the quantum vacuum. All these components are referred to as ‘partons’. In the standard picture of proton–proton (pp) collisions, typically only a few partons undergo a hard scattering with one another, with the remainders of each proton only slightly disturbed in the process. As the collision energy increases, the densities of gluons and sea quarks probed inside each proton grow rapidly. Thus, at high enough energies, more than one pair of partons can undergo a hard scattering in a single pp collision, leading to the simultaneous and independent production of two or more particles with transverse momentum (p_T) and/or mass (m) above a few gigaelectronvolts. Double-parton scatterings (DPS) were first observed at the CERN Intersecting Storage Rings some 35 years ago^1,2 and have been a subject of intense theoretical and experimental investigations ever since³. Numerous DPS processes have been studied in measurements with many combinations of pairs of heavy and/or high-p_T produced particles³. Triple-parton scatterings (TPSs), where three hard parton interactions take place simultaneously, have been proposed for study only recently⁴ and have not been experimentally explored yet. Studies of n-parton scattering (NPS) processes are important to elucidate the complicated inner structure of the proton and its evolution with energy^5,6. Many of these features, for example, the parton density profile in the plane transverse to the colliding beams, as well as the various correlations (in position, momentum, flavour, colour, spin and so on) between individual partons, are very difficult to calculate theoretically, and can only be mapped out through experimental studies of NPS in different systems and for different numbers n of simultaneous scatterings³.

Measurements of such processes not only allow for a deeper understanding of the proton structure but also are of relevance at the LHC to predict backgrounds in rare standard-model processes, and in searches for new physics, in final states where multiple heavy particles are produced^7,8. This Article presents the experimental study of the simultaneous production of three massive particles originating in NPS, and the observation of triple-J/ψ meson production. The study of TPS via triple-J/ψ production provides input for further theoretical and experimental progress in understanding the NPS dynamics.

In the simplest approach, ignoring any correlations between the individual partons, the probability to produce n high-p_T particles in a given pp collision must be proportional to the nth product of probabilities to independently produce each of them. Thus, the probability to produce two or three high-p_T particles in DPS and TPS scales with the square and cube, respectively, of the corresponding single-parton scattering (SPS) probabilities⁹. The occurrence of DPS and TPS processes is therefore more likely for final states with large SPS cross-sections, such as quarkonia states (for example, J/ψ and ϒ mesons), than for rarer heavier particles, such as electroweak bosons¹⁰. In the DPS case, the cross-section to produce, for example, two charmonium mesons ψ₁ and ψ₂ can be written as the product of the SPS cross-sections for the production of each individual meson divided by an effective cross-section to warrant the proper units of the final result

$${\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{pp}}}}\rightarrow \psi {}_{1}\psi {}_{2}+{{X}}\,}=\left(\frac{{\mathfrak{m}}}{2}\right)\frac{{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{pp}}}}\rightarrow \psi {}_{1}+{{X}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{pp}}}}\rightarrow \psi {}_{2}+{{X}}}}{{\sigma }_{{{{\rm{eff}}}},{{{\rm{DPS}}}}}}.$$

(1)

Here, ${\mathfrak{m}}$ is a combinatorial factor to avoid double counting, ${\mathfrak{m}}=1\,(2)$ if ψ₁ = ψ₂ (ψ₁ ≠ ψ₂), and σ_eff,DPS is an effective cross-section that, in a purely geometric approach, can be determined from the pp transverse overlap⁹. A smaller value of σ_eff,DPS, which is proportional to the average (squared) transverse separation of the partons participating in the two hard scatterings, implies larger DPS yields.

For the proton form factors typically implemented in the Pythia 8¹¹ and Herwig++¹² event generators commonly used in collider physics, values of σ_eff,DPS ≈ 20–30 mb are expected. Such estimates are, however, about a factor of two larger than those experimentally derived via the ratio ${\sigma }_{{{{\rm{eff}}}},{{{\rm{DPS}}}}}=({\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{pp}}}}\rightarrow {{X}}{}_{1}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{pp}}}}\rightarrow {{X}}{}_{2}})/{\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{pp}}}}\rightarrow {{{\rm{X}}}}{}_{1}{{{\rm{X}}}}{}_{2}}$ for processes involving pairs of high-p_T jets and/or electroweak bosons, which are found to lie in the range σ_eff,DPS ≈ 10–20 mb (refs. ^{13,14,15,16,17,18,19}). This discrepancy has been mostly explained as evidence of parton correlations in the collision not accounted for in the purely geometrical approaches²⁰. In addition, significantly lower σ_eff,DPS ≈ 3–10 mb values have been extracted from measurements of quarkonium pair production (J/ψJ/ψ (refs. ^{21,22,23,24,25}), J/ψϒ (ref. ²⁶) and ϒϒ (refs. ^8,27)) that have been interpreted as due to the different dominant species (mostly gluons for quarkonia, and quarks for electroweak bosons) in the parton distribution functions (PDFs) probed in the different scatterings³, but can be also attributed in some cases to poorly controlled subtractions of SPS contributions¹⁰.

The study of TPS via triple-J/ψ production can help solve all the issues mentioned above. The equivalent of equation (1) for the production of three charmonium mesons in a TPS process reads

$${\sigma }_{{{{\rm{TPS}}}}}^{{{{\rm{pp}}}}\rightarrow \psi {}_{1}\psi {}_{2}\psi {}_{3}+{{X}}}=\left(\frac{{\mathfrak{m}}}{3!}\right)\frac{{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{pp}}}}\rightarrow \psi {}_{1}+{{X}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{pp}}}}\rightarrow \psi {}_{2}+{{X}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{pp}}}}\rightarrow \psi {}_{3}+{{X}}}}{{\sigma }_{{{{\rm{eff}}}},{{{\rm{TPS}}}}}^{2}},$$

(2)

where ${\mathfrak{m}}$ = 1, 3 or 6 (depending on whether all three, two or none of the ψ_i states are identical). In the absence of parton correlations, the effective cross-section σ_eff,TPS is closely related to its DPS counterpart via σ_eff,TPS = κσ_eff,DPS, with κ of order unity. A value of κ = 0.82 ± 0.11 has been derived in ref. ⁴ for a variety of proton transverse parton profiles. A theoretical study of the production of three prompt-J/ψ mesons²⁸, based on the non-relativistic quantum chromodynamics approach at leading-order (LO) accuracy as implemented in the HELAC-Onia code^29,30, has demonstrated that the pure SPS contributions are negligible compared with those from DPS and TPS. Namely, the top left diagram of Fig. 1 is irrelevant compared with the two other diagrams in the left column of the figure. The experimental measurement of pp → J/ψ J/ψ J/ψ X is thus a golden channel for the study of TPS and, in addition, provides an alternative extraction of σ_eff,DPS, thereby shedding light on the underlying dynamics of hard NPS. The production of J/ψ states can also proceed non-promptly through the decay of a beauty-quark (b) hadron. Notwithstanding a small branching fraction, ${{{{\mathcal{B}}}}}_{{{b}}\rightarrow {{J}}/\psi {{X}}}\approx 1 \%$ (ref. ³¹), the cross-section to produce ${{b}}\bar{{{b}}}$ pairs is large at the LHC, $\sigma ({{{\rm{pp}}}}\rightarrow {{b}}\bar{{{b}}}\,{{X}})\approx 0.5\,{{{\rm{mb}}}}$ (ref. ⁴). The contributions of such processes to inclusive triple-J/ψ production are schematically shown in Fig. 1 (diagrams to the right of the vertical dashed line).

Fig. 1: Leading-order diagrams for inclusive triple-J/ψ production in pp collisions.

The SPS, DPS and TPS processes are depicted in the top, middle and bottom rows, respectively. The leftmost diagrams show triple prompt-J/ψ processes. The remaining diagrams show (left to right) final states with increasing contributions of non-prompt-J/ψ mesons from beauty hadron decays. Curly lines indicate gluons, arrows indicate (anti)charm quarks and ovals indicate the proton parton densities. The symbols ${\sigma }_{{{{\rm{NPS}}}}}^{i\,{{{\rm{p}}}}\,j\,{{{\rm{np}}}}}$ identify the number (i and j) of prompt (p) and non-prompt (np) contributions to the cross-section of each diagram.

This Article reports the observation of the simultaneous production of three J/ψ mesons in pp collisions. The analysis is based on a data sample collected at $\sqrt{s}=13\,{{{\rm{TeV}}}}\,$ by the Compact Muon Solenoid (CMS) experiment, corresponding to an integrated luminosity of 133 fb⁻¹. The J/ψ mesons are reconstructed in their dimuon decay mode over a fiducial phase space in transverse momenta (p_T^μ,^J/ψ) and (pseudo)rapidities (|η^μ| and |y^J/ψ|) defined to maximize the signal purity and the detector acceptance and efficiency. The analysis of the 6μ final state offers a very clean experimental signature for inclusive triple-J/ψ production, comprising prompt and non-prompt components. Methods provides more details on the experimental set-up and event reconstruction (the J/ψ candidates passing the triple-J/ψ selection criteria are shown in Extended Data Table 1).

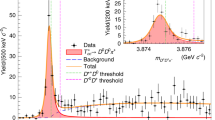
The signal yield is extracted with a three-dimensional unbinned extended maximum likelihood fit of the ${m}_{{\mu }^{+}{\mu }^{-}}$ distributions of all J/ψ candidates in the event over the $2.9\,{\rm{GeV}} < {m}_{{\mu }^{+}{\mu }^{-}} < 3.3\,{{{\rm{GeV}}}}$ range. The expected J/ψ mass peaks are modelled with a Gaussian function with mean fixed to their nominal value (m^J/ψ = 3.097 GeV)³¹ and the root-mean-square (RMS) width fixed to the resolution derived from the Monte Carlo (MC) simulation (σ_m ≈ 30 MeV). Given the very low number of events passing the selection, the mass mean and RMS width of the J/ψ mesons cannot be left as free parameters in the fit. The dimuon background is described with an exponential function^{23,32,33,34,35}. The fit has eight free parameters for the yields given by the combination of each of the three J/ψ candidates as being either signal or background. The extracted signal yield (red shaded areas in the ${m}_{{\mu }^{+}{\mu }^{-}}$ distributions of Fig. 2) corresponds to ${N}_{{{{\rm{sig}}}}}^{3{{J}}/\psi}=5.{0}_{-1.9}^{+2.6}$ triple-J/ψ events, with $1.{0}_{-0.8}^{+1.4}$ background events. The statistical significance of the signal is evaluated using various methods. From the likelihood ratio of two fits (background-only imposing ${N}_{{{{\rm{sig}}}}}^{3{{J}}/\psi }=0$, and the default signal-plus-background), with the standard asymptotic formula³⁶ assuming that the conditions to apply Wilks’ theorem³⁷ are satisfied, a significance of 6.7 standard deviations (s.d.) is obtained. The significance derived assuming a Poisson counting experiment yields 5.8 s.d., and it is found to be above 5.5 s.d. by using MC pseudoexperiments.

Fig. 2: Invariant mass distributions for the three μ⁺μ⁻ pairs in the selected events.

The three distributions are ordered, left to right, by decreasing pair p_T. The data are represented by the points with the vertical bars showing the (Poisson) statistical uncertainties. The solid (dotted) curve shows the overall fit to the data (in the extended mass range, discussed in the main text), and the red shaded area shows the fitted signal yield. The horizontal bin width is indicated on the vertical axis legend.

To cross-check the size of the combinatorial background derived from the fit, two tests are carried out. First, the fit is repeated over the extended dimuon mass range [2.5–3.3] GeV for the two subleading J/ψ mesons (dotted curves in Fig. 2). This mass range corresponds to an asymmetric window of about [−20σ_m, +7σ_m] around the J/ψ nominal mass that, as aforementioned, covers lower dimuon masses where the background, if any, should be larger. The obtained signal yield is fully consistent with the default result. A second test is performed whereby the opposite-sign (OS) requirement is removed to allow also for same-sign dimuon combinations (μ^±μ^±) for the two subleading pairs. After applying the rest of the selection criteria of the default analysis, no triplet events containing same-sign muon pairs are observed.

To estimate the average prompt and non-prompt contributions in the triple-J/ψ events, the proper decay length of each J/ψ is calculated as ${L}^{{{J}}/\psi }=({m}^{{{J}}/\psi }/{p}_{{{{\rm{T}}}}}^{{{J}}/\psi}){L}_{xy}^{{{J}}/\psi }$, where ${L}_{xy}^{{{J}}/\psi}=({\bf{r}}\cdot {{\bf{{p}}_{{{{\rm{T}}}}}}}^{{{J}}/\psi })/| {p}_{{{{\rm{T}}}}}^{{{J}}/\psi }|$ is the transverse distance between the J/ψ decay vertex and the primary pp interaction vertex (PV) (r is the vector from the PV to the J/ψ vertex). The experimental resolution on L^J/ψ is about 20 μm. Prompt-J/ψ mesons are defined as those having L^J/ψ < 60 μm, a choice that reduces the non-prompt contribution by more than one order in magnitude³³. A signal-only subset of events is defined based on all J/ψ candidates found in a narrower invariant mass region, within ±3 s.d. around m^J/ψ, than that used in the default signal extraction. In this range, five triple-J/ψ events are found that can be classified as two events being consistent with the ‘2 non-prompt + 1 prompt J/ψ’ hypothesis, and one event each in the ‘1 non-prompt + 2 prompt J/ψ’, ‘3 non-prompt J/ψ’ and ‘3 prompt J/ψ’ categories. Such a classification is confirmed with a second method where prompt and non-prompt weights are extracted with the sPlot technique³⁸, exploiting an unbinned maximum likelihood fit of the L^J/ψ distributions.

The cross-section for inclusive triple-J/ψ production measured in the fiducial region defined in Table 1 is obtained via $\sigma \left({{{\rm{pp}}}}\rightarrow {{J}}/\psi \,{{J}}/\right.$$\psi \,{{J}}/\psi \,{{X}}\left.\right)={N}_{{{{\rm{sig}}}}}^{3{{J}}/\psi }/(\epsilon {{{\mathcal{L}}}}{}_{{{{\rm{int}}}}}{{{{\mathcal{B}}}}}_{{{J}}/\psi \rightarrow {\mu }^{+}{\mu }^{-}}^{3})$, where ${N}_{{{{\rm{sig}}}}}^{3{{J}}/\psi}$ is the number of signal events, ${{{\mathcal{L}}}}{}_{{{{\rm{int}}}}}$ is the total integrated luminosity, ${{{{\mathcal{B}}}}}_{{{J}}/\psi \rightarrow {\mu}^{+}{\mu }^{-}}$ is the dimuon branching fraction and ϵ = ϵ_triϵ_idϵ_reco is the total efficiency composed of trigger, identification and reconstruction components, respectively. The J/ψ muon identification and reconstruction efficiencies are extracted with the tag-and-probe method using correction factors from the large inclusive J/ψ → μ⁺μ⁻ data samples used in ref. ³⁹. As they depend on the p_T and η of the muons, they propagate into the final cross-section via two-dimensional maps, yielding ϵ_idϵ_reco = 0.78. The trigger efficiency is found to be ϵ_trig = 0.84 from a study of the MC samples.

Table 1 Fiducial phase space for the triple-J/ψ cross-section measurement

The impact on the extracted cross-section of the choice of functions used to reproduce the shapes of the signal and background dimuon invariant masses is studied. For the signal, the Gaussian distribution is changed to a Crystal-Ball function⁴⁰ as well as to a Gaussian function with the RMS width left to vary in the fit. The background shape is changed from the default exponential to first- and zeroth-order polynomials. The relative differences in the cross-sections obtained from the alternative modelling for signal and background are 0.8% and 3.4%, respectively, and are assigned as corresponding systematic uncertainties. Uncertainties arising from the muon reconstruction and identification efficiencies are derived by allowing the tag-and-probe correction factors for each (p_T, η) bin to vary within their precision, and checking the effect on the extracted cross-section. The maximal variation observed is ±1.0%. Varying the relative composition of double- and single-J/ψ meson production in the MC event sample used for the determination of the trigger efficiency leads to a 3.4% propagated uncertainty. Uncertainties of 1.6% and 3.0% are added from the integrated luminosity measurement^41,42,43, and from the simulated signal sample size, respectively. The uncertainty in the ${{{{\mathcal{B}}}}}_{{{J}}/\psi \rightarrow {\mu }^{+}{\mu }^{-}}=(5.961\pm 0.033) \%$ value^31,32,33 propagates into a 1.7% uncertainty in the cross-section. The total systematic uncertainty of the measured cross-section is 6.2%, obtained by adding all individual sources in quadrature (Extended Data Table 2). The measured cross-section for triple-J/ψ production, within the fiducial region defined in Table 1, is $\sigma ({{{\rm{pp}}}}\rightarrow {{J}}/\psi \,{{J}}/\psi \,{{J}}/\psi \,{{X}})=27{2}_{-104}^{+141}\,{{{\rm{(stat)}}}}\pm 17\,{{{\rm{(syst)}}}}\,{{{\rm{fb}}}}$.

The total inclusive triple-J/ψ cross-section is expected to correspond to the sum of the contributions from the SPS, DPS and TPS processes schematically shown in Fig. 1, each of which contains various combinations of prompt (p) and non-prompt (np) J/ψ contributions

$$\begin{array}{lll}{\sigma }_{{{{\rm{tot}}}}}^{3{{J}}/\psi}&=&{\sigma }_{{{{\rm{SPS}}}}}^{3{{J}}/\psi}+{\sigma }_{{{{\rm{DPS}}}}}^{3{{J}}/\psi}+{\sigma }_{{{{\rm{TPS}}}}}^{3{{J}}/\psi }\\ &=&\left({\sigma }_{{\rm{SPS}}}^{{{{\rm{3}\,{p}}}}}+{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{2}\,{p}\,{1}\,{np}}}}}+{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}\,{2}\,{np}}}}}+{\sigma }_{{{{\mathrm{SPS}}}}}^{{{{\rm{3}\,{np}}}}}\right)\\ &+&\left({\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{3}\,{p}}}}}+{\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{2}\,{p}\,{1}\,{np}}}}}+{\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{1}\,{p}\,{2}\,{np}}}}}+{\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{3}\,{np}}}}}\right)\\ &+&\left({\sigma }_{{{{\rm{TPS}}}}}^{{{{\rm{3}\,{p}}}}}+{\sigma }_{{{{\rm{TPS}}}}}^{{{{\rm{2}\,{p}\,{1}\,{np}}}}}+{\sigma }_{{{{\rm{TPS}}}}}^{{{{\rm{1}\,{p}\,{2}\,{np}}}}}+{\sigma }_{{{{\rm{TPS}}}}}^{{{{\rm{3}\,{np}}}}}\right).\end{array}$$

(3)

Under the simplest assumption of factorization of multiple hard-scattering probabilities in terms of SPS cross-sections, the DPS and TPS contributions to triple-J/ψ production (last row of equation (3)) can be written through equations (1) and (2) as a combination of products of single- and double-J/ψ SPS cross-sections as

$$\begin{array}{lll}{\sigma }_{{{{\rm{DPS}}}}}^{3{{J}}/\psi }&=&\frac{{{\mathfrak{m}}}_{1}}{{\sigma }_{{{{\rm{eff}}}},{{{\rm{DPS}}}}}}\\ &\times &\left[{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{2}\,{p}}}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}+{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{2}\,{p}}}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{np}}}}}+{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}\,{1}\,{np}}}}}\right.\\ &+&\left.{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}\,{1}\,{np}}}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{np}}}}}+{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{2}\,{np}}}}}+{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{2}\,{np}}}}}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{np}}}}}\right],\end{array}$$

(4)

and

$$\begin{array}{lll}{\sigma }_{{{{\rm{TPS}}}}}^{3{{J}}/\psi }&=&\frac{{{\mathfrak{m}}}_{3}}{{\sigma }_{{{{\rm{eff}}}},{{{\rm{TPS}}}}}^{2}}\left[{\left({\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}\right)}^{3}+{\left({\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{np}}}}}\right)}^{3}\right]\\ &+&\frac{{{\mathfrak{m}}}_{2}}{{\sigma }_{{{{\rm{eff}}}},{{{\rm{TPS}}}}}^{2}}\left[{\left({\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}\right)}^{2}{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{np}}}}}+{\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}{\left({\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{np}}}}}\right)}^{2}\right],\end{array}$$

(5)

with combinatorial prefactors ${{\mathfrak{m}}}_{1}=2/2=1$, ${{\mathfrak{m}}}_{2}=3/3!=1/2$ and ${{\mathfrak{m}}}_{3}=1/3!=1/6$. Therefore, from the eight individual SPS cross-sections for single-, double- and triple-J/ψ production, one can determine the total triple-J/ψ production cross-section via equations (3)–(5). The values of the relevant SPS cross-sections, each within the fiducial phase space defined in Table 1, are computed as described next and listed in Table 2.

Table 2 Theoretical J/ψ, J/ψ + J/ψ, and J/ψ + J/ψ + J/ψ cross-sections

The values of the SPS single, double and triple prompt-J/ψ cross-sections (${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}$, ${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{2}\,{p}}}}}$ and ${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{3}\,{p}}}}}$) are obtained with HELAC-Onia at LO or at approximately next-to-leading-order (NLO*) accuracy^44,45. For the single prompt-J/ψ prediction (${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{p}}}}}$), the theoretical calculations HO(data) in Table 2 are normalized with a parameterization⁴⁶ that reproduces the data measured in pp collisions at 7 TeV (refs. ^34,47), including all feed-down contributions from decays of heavier charmonium resonances. For the double and triple prompt-J/ψ processes, the HELAC-Onia calculations include only the ψ(2S) feed-down because the χ_c decay contribution is only a few percent. All predictions for cross-sections of non-prompt-J/ψ meson production in beauty hadron decays (${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{1}\,{np}}}}}$, ${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{2}\,{np}}}}}$ and ${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{3}\,{np}}}}}$) have been obtained with MadGraph 5_aMC@NLO (v.2.6.6)⁴⁸ matrix elements, scaled by a factor of 1.15 to account for next-to-next-to-leading-order ${{b}}\bar{{{b}}}$ cross-section corrections⁴, combined with the Pythia 8.244 generator for parton shower and decays (including all feed-down quarkonium contributions)⁴⁵. Mixed prompt plus non-prompt cross-sections (${\sigma }_{{{{\rm{SPS}}}}}^{{{X\,{\rm{p}}\,Y\,{\rm{n}}}}}$) are obtained from ${{J}}/\psi+{{b}}\bar{{{b}}}$ events generated with HELAC-Onia at LO in the colour-singlet model interfaced with Pythia 8.244 for the b quarks fragmentation into non-prompt-J/ψ mesons. The uncertainties include the (dominant) theoretical scale dependence and the (subdominant) PDF uncertainties of the CT14NLO set⁴⁹, except for the single prompt-J/ψ predictions that have a better precision because they are determined with an explicit fit of the non-relativistic quantum chromodynamics predictions to the LHC data⁴⁶ and have an associated 10% uncertainty of experimental origin. All these sources are treated as uncorrelated and the corresponding uncertainties are added in quadrature.

Using equations (4) and (5) with the SPS cross-sections listed in Table 2, and assuming that the effective DPS and TPS cross-sections are related by σ_eff,TPS = (0.82 ± 0.11) σ_eff,DPS (ref. ⁴) in a baseline approach that ignores parton correlations, one can extract the value of the effective DPS cross-section that yields the experimentally measured ${\sigma }_{{{{\rm{tot}}}}}^{3{{J}}/\psi}$ value. Following such a procedure, the value ${\sigma }_{{{{\rm{eff}}}},{{{\rm{DPS}}}}}=2.{7}_{-1.0}^{+1.4}\,(\exp ){\,}_{-1.0}^{+1.5}\,{{{\rm{(theo)}}}}\,{{{\rm{mb}}}}$ is derived, where the first uncertainty is due to the experimental ${\sigma }_{{{{\rm{tot}}}}}^{3{{J}}/\psi}$ precision and the second is due to the propagation of all sources of theoretical uncertainties in the ingredients of equations (3)–(5).

The inclusive triple-J/ψ theoretical cross-sections and yields for each individual process contributing to the total production are listed in Table 3. The expected contributions from SPS, DPS and TPS processes to the total triple-J/ψ cross-section amount to about 6%, 74% and 20%, respectively. This confirms the conclusion of ref. ²⁸ that triple-J/ψ production is a golden channel to study DPS and TPS, with minimal SPS contamination. The largest contributors to the triple-J/ψ cross-section are ${\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{3}\,{np}}}}}$ and ${\sigma }_{{{{\rm{DPS}}}}}^{{{{\rm{1}\,{p}\,{2}\,{np}}}}}$, accounting for about 33% each, ${\sigma }_{{{{\rm{TPS}}}}}^{{{{\rm{2}\,{p}\,{1}\,{np}}}}}$ and ${\sigma }_{{{{\rm{TPS}}}}}^{{{{\rm{1}\,{p}\,{2}\,{np}}}}}$ amounting to about 7% each, and ${\sigma }_{{{{\rm{SPS}}}}}^{{{{\rm{3}\,{np}}}}}$ representing about 4% of the total production. In terms of prompt and non-prompt contributions, the theoretical expectation for the production of three promptly produced J/ψ mesons is about 5% of the total yield, whereas the percentage expected for three non-prompt-J/ψ mesons is about 45%. The remaining half of the triple-J/ψ events are expected to be due to the combination of J/ψ mesons produced promptly and from beauty hadron decays. This result is consistent, within the large statistical uncertainties of the present dataset, with the combination of prompt and non-prompt-J/ψ mesons derived from the decay length of each dimuon candidate.

Table 3 Expected contributions to triple-J/ψ production

In Fig. 3, the σ_eff,DPS value extracted here (red circle) is compared with the world data on effective DPS cross-sections derived from midrapidity measurements with quarkonium final states^{22,22,24,24,25,26,50} (blue symbols), as well as from processes with jets, photons and/or W bosons^{13,14,15,16,17,18,19,51,52,53,54,55,56} (black symbols). A few of the σ_eff,DPS values plotted have been derived by more advanced phenomenological studies^57,58,59,60 of the experimental quarkonium data. The effective cross-sections obtained from quarkonium measurements favour a smaller value of σ_eff,DPS ≈ 3–10 mb compared with the σ_eff,DPS ≈ 10–20 mb derived from harder or heavier final states. Such an apparent process-dependent σ_eff,DPS value is suggestive of different parton transverse profiles, and/or correlations present, probed inside the proton at varying fractional momenta, given by $x=\sqrt{{{p}^2_{{{\rm{T}},{V}}}}+{m}_{{{V}}}^{2}}\,{{{{\rm{e}}}}}^{\eta }/\sqrt{s}$, for V = J/ψ, ϒ, W, Z. At midrapidity (|η| < 2.5), quarkonia are produced mostly in gluon–gluon scatterings carrying a fraction x ≈ 5 × 10⁻⁴ of the proton momentum, whereas mostly quarks with x ≈ 10⁻² participate in the production of electroweak bosons. The fact that LHCb measurements of double-quarkonia and quarkonia-plus-charm^25,61 at forward rapidities (η ≈ 2–4.5), processes that originate in parton scatterings with asymmetric fractional momenta x₁ ≈ 10⁻⁴ and x₂ ≈ 10⁻², lead to values of σ_eff,DPS ≈ 15 mb, larger than those measured at midrapidity for similar final states, seems to confirm the dependence of the effective DPS cross-section on the relevant parton species and x fractions probed.

Fig. 3: Comparison of σ_eff,DPS parameters extracted in various processes.

The result obtained here (top red circle) is compared with those derived in midrapidity measurements of double-quarkonium and electroweak-boson-plus-quarkonium production^{22,24,25,57,58,59,60} (blue symbols), as well as in final states with jets^19,51,52,62, γ + jets^53,54,55,56, W + jets^13,14 and same-sign W bosons¹⁸ (black symbols). The arrows indicate lower (or upper) limits at 95% (68%) confidence level. For the experimental results marked with a star, more recent theoretical reinterpretations based on more accurate calculations of the corresponding SPS cross-section are plotted. The original experimental results can be found in ref. ²³ (CMS), ref. ²⁶ (D0) and refs. ^50,63 (ATLAS).

Methods

Experimental set-up

The central feature of the CMS apparatus is a superconducting solenoid of 6 m internal diameter, providing a magnetic field of 3.8 T. Within the solenoid volume are a silicon pixel and strip tracker, a lead tungstate crystal electromagnetic calorimeter, and a brass and scintillator hadron calorimeter, each composed of a barrel and two endcap sections. Forward calorimeters extend the η coverage provided by the barrel and endcap detectors. Muons are measured over the range |η| < 2.4 in gas-ionization detectors, embedded in the steel flux-return yoke outside the solenoid, made using three technologies: drift tubes, cathode strip chambers and resistive plate chambers. A more detailed description of the CMS detector can be found in ref. ⁶⁴.

Events of interest are selected using a two-tiered trigger system. The first trigger level, composed of custom hardware processors, uses information from the calorimeters and muon detectors to select events at a rate of around 100 kHz with a fixed latency of about 4 μs (ref. ⁶⁵). The second level (or high-level trigger, HLT) consists of a farm of processors running a version of the full event reconstruction software optimized for fast processing, and reduces the event rate to around 1 kHz before data storage⁶⁶. The present analysis employs an HLT that requires three muons, each having p_T > 3.5 GeV for |η| < 1.2 (barrel) or p_T > 2.5 GeV for 1.2 < |η| < 2.4 (endcap). In addition, the event must have at least one pair of oppositely charged muons with invariant mass between 2.80 GeV and 3.35 GeV that originate from a common vertex with a probability greater than 0.5%, as determined by a Kalman vertex fit⁶⁷, thus suppressing random combinations of muons from unrelated sources. MC simulations are used to determine the trigger efficiency. Simulated events are generated using HELAC-Onia (v.2.6.6) with the NNPDF3.0 PDF set⁶⁸, and Pythia 8.205 for the hadronization and decay with the CUETP8M1 underlying event tune⁶². Triple-J/ψ events are simulated by combining events from two different MC samples with varying relative fractions. The first MC sample contains three singly produced J/ψ mesons, whereas the second sample combines single- and double-J/ψ meson production, following ref. ²⁸. As the J/ψ mesons originating in both processes have slightly different p_T spectra, the variation of their relative fractions in the simulation allows to effectively scan the triple-muon trigger efficiency in the more uncertain region close to the trigger p_T thresholds. The generated events are then processed through a detailed Geant4 simulation⁶⁹ of the CMS detector response.

Event reconstruction and selection

Muons are reconstructed by combining information from the silicon tracker and the muon system³⁹. The matching between tracks reconstructed in each of the subsystems proceeds either outside-in, starting from a track in the muon system, or inside-out, starting from a track provided by the silicon tracker. Matching muons to tracks measured in the silicon tracker leads to a relative p_T resolution of 1% in the barrel and 3% in the endcaps for muons with p_T up to 100 GeV (ref. ³⁹). The candidate vertex with the largest value of summed physics-object p_T² in the event is taken to be the PV⁷⁰. Only charged particles that are either directly participating in the PV determination, or are closest to the PV along the z direction and not used in any other PV identification (namely, they are consistent with secondary decays from the closest PV), are used in the analysis. Simulation studies show that this procedure efficiently suppresses any potential contamination from charged particles produced in any other pp collision taking place in the same bunch crossing (pile-up).

The offline data analysis starts by selecting events with six or more reconstructed muons, each passing the p_T and η criteria implemented at the HLT. The muons are combined into OS pairs, and are considered for further study if their invariant mass is $2.9\,{\rm{GeV}} < {m}_{{\mu }^{+}{\mu }^{-}} < 3.3\,{{{\rm{GeV}}}}$ (corresponding to about ±7 times the J/ψ mass resolution discussed below) and originate from a common vertex with a probability greater than 0.5%, thereby reducing the random pairing of muons originating from other background sources in the same event, as discussed below. All selected muon pairs are further required to share the same PV (including the possibility that they originate from secondary vertices associated to a common PV) to eliminate accidental combinations of muons from different pp collisions in the same or neighbouring bunch crossings. The analysis thereby includes prompt-J/ψ mesons coming directly from the pp interaction (or from feed-down decays of promptly produced and decayed resonances), and non-prompt ones coming from the decays of beauty hadrons. To ensure high purity and reconstruction efficiency, the J/ψ candidates are required to have p_T > 6 GeV and |y| < 2.4.

After applying the selection criteria discussed above, six triple-J/ψ events are observed. No alternative pairings among the OS muons in these six events are found to satisfy the analysis requirements. In all events, the J/ψ meson with highest p_T (‘leading’ J/ψ) is found to correspond to the muon pair that passed the online trigger selection. In inclusive J/ψ measurements^{23,32,33,34,35}, a continuum background is present in the ${m}_{{\mu }^{+}{\mu }^{-}}$ distribution due to random combinations of OS muons originating from semileptonic beauty- and charm-quark hadron decays, b → μ + X and c → μ + X, and Drell–Yan events, which pass the trigger and data analysis criteria. To monitor the sideband background population, the mass windows corresponding to the two subleading J/ψ mesons are extended well below the J/ψ mass region. The corresponding dimuon invariant mass distributions are shown in Fig. 2 ordered (left to right) by decreasing p_T of the μ⁺μ⁻ system. Only one additional background event is found in the extended mass region indicated by the dotted curves, confirming that the combinatorial continuum is suppressed by the requirement of having three reconstructed J/ψ candidates in the same event.

Event kinematic properties

Detailed information of the kinematic properties of the J/ψ candidates passing the triple-J/ψ selection criteria are shown in Extended Data Table 1. The kinematic distributions of all six J/ψ triplets do not show any local peak, which could be indicative of, for example, a resonance decaying into three J/ψ mesons, but are distributed featureless (with large point-to-point statistical uncertainties) over triple-J/ψ mass, p_T and η.

All sources of systematic uncertainty in the triple-J/ψ cross-section measurement are listed in Extended Data Table 2.