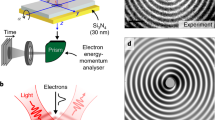
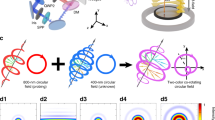
Abstract
Circular dichroism (CD) describes the different responses of a chiral object to circularly polarized light of opposite handedness and serves as the basis of most chirality-sensitive spectroscopy techniques. All previously observed CD effects originate from the chiral sensitivity of the amplitudes of transition-matrix elements. However, CD effects in the phase of such matrix elements have barely been studied, even theoretically. Here we present a combined experimental and theoretical investigation of amplitude- and phase-resolved CDs of continuum–continuum transitions for electron vortices. We employ a circularly polarized attosecond pulse train to prepare electron vortices in the continuum, and a circularly polarized near-infrared laser pulse to probe the chirality of the electron vortices. Our complete experimental reconstruction of the partial-wave amplitudes and phases demonstrates that the photoionization time delays of the continuum–continuum transitions depend not only on the angular-momentum quantum number l of the populated continuum state, but also on its magnetic quantum number m. Our work defines a general technique called attosecond circular-dichroism chronoscopy (ACDC), which can provide new insights into electron-vortex beams, chiral molecules and magnetic materials on the most fundamental timescales.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Uchida, M. & Tonomura, A. Generation of electron beams carrying orbital angular momentum. Nature 464, 737–739 (2010).
Djiokap, J. N. et al. Electron vortices in photoionization by circularly polarized attosecond pulses. Phys. Rev. Lett. 115, 113004 (2015).
Ngoko Djiokap, J. M. et al. Multistart spiral electron vortices in ionization by circularly polarized uv pulses. Phys. Rev. A 94, 013408 (2016).
Pengel, D., Kerbstadt, S., Englert, L., Bayer, T. & Wollenhaupt, M. Control of three-dimensional electron vortices from femtosecond multiphoton ionization. Phys. Rev. A 96, 043426 (2017).
Pengel, D. et al. Electron vortices in femtosecond multiphoton ionization. Phys. Rev. Lett. 118, 053003 (2017).
Ngoko Djiokap, J. M. et al. Dynamical electron vortices in attosecond double photoionization of H2. Phys. Rev. A 98, 063407 (2018).
Eckart, S. et al. Ultrafast preparation and detection of ring currents in single atoms. Nat. Phys. 14, 701–704 (2018).
Han, M. et al. Probing photoionization dichroism of excited electron ring currents by chiral photoelectron spectroscopy. Phys. Rev. A 101, 043406 (2020).
Herath, T., Yan, L., Lee, S. K. & Li, W. Strong-field ionization rate depends on the sign of the magnetic quantum number. Phys. Rev. Lett. 109, 043004 (2012).
Tolstikhin, O. I. & Morishita, T. Strong-field ionization, rescattering and target structure imaging with vortex electrons. Phys. Rev. A 99, 063415 (2019).
Verbeeck, J., Tian, H. & Schattschneider, P. Production and application of electron vortex beams. Nature 467, 301–304 (2010).
Hartung, A. et al. Electron spin polarization in strong-field ionization of xenon atoms. Nat. Photon. 10, 526–528 (2016).
Fleischer, A., Kfir, O., Diskin, T., Sidorenko, P. & Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photon. 8, 543–549 (2014).
Kfir, O. et al. Generation of bright phase-matched circularly-polarized extreme ultraviolet high harmonics. Nat. Photon. 9, 99–105 (2014).
Hickstein, D. D. et al. Non-collinear generation of angularly isolated circularly polarized high harmonics. Nat. Photon. 9, 743–750 (2015).
Huang, P.-C. et al. Polarization control of isolated high-harmonic pulses. Nat. Photon. 12, 349–354 (2018).
Li, R., Sullivan, R., Al-Basheer, W., Pagni, R. & Compton, R. Linear and nonlinear circular dichroism of R-(+)-3-methylcyclopentanone. J. Chem. Phys. 125, 144304 (2006).
Pitzer, M. et al. Direct determination of absolute molecular stereochemistry in gas phase by coulomb explosion imaging. Science 341, 1096–1100 (2013).
Herwig, P. et al. Imaging the absolute configuration of a chiral epoxide in the gas phase. Science 342, 1084–1086 (2013).
Böwering, N. et al. Asymmetry in photoelectron emission from chiral molecules induced by circularly polarized light. Phys. Rev. Lett. 86, 1187–1190 (2001).
Garcia, G. A. et al. Circular dichroism in the photoelectron angular distribution from randomly oriented enantiomers of camphor. J. Chem. Phys. 119, 8781–8784 (2003).
Baykusheva, D. & Wörner, H. J. Chiral discrimination through bielliptical high-harmonic spectroscopy. Phys. Rev. X 8, 031060 (2018).
Neufeld, O. et al. Ultrasensitive chiral spectroscopy by dynamical symmetry breaking in high harmonic generation. Phys. Rev. X 9, 031002 (2019).
Corkum, P. B. & Krausz, F. Attosecond science. Nat. Phys. 3, 381–387 (2007).
Hentschel, M. et al. Attosecond metrology. Nature 414, 509–513 (2001).
Itatani, J. et al. Attosecond streak camera. Phys. Rev. Lett. 88, 173903 (2002).
Paul, P. M. et al. Observation of a train of attosecond pulses from high harmonic generation. Science 292, 1689–1692 (2001).
Klünder, K. et al. Probing single-photon ionization on the attosecond time scale. Phys. Rev. Lett. 106, 143002 (2011).
Huppert, M., Jordan, I., Baykusheva, D., von Conta, A. & Wörner, H. J. Attosecond delays in molecular photoionization. Phys. Rev. Lett. 117, 093001 (2016).
Han, M. et al. Attosecond metrology in circular polarization. (2022). https://doi.org/10.48550/arXiv.2211.02769
Ullrich, J. et al. Recoil-ion and electron momentum spectroscopy: reaction-microscopes. Rep. Prog. Phys. 66, 1463–1545 (2003).
Dörner, R. et al. Cold Target Recoil Ion Momentum Spectroscopy: a ‘momentum microscope’ to view atomic collision dynamics. Phys. Rep. 330, 95–192 (2000).
Heck, S. et al. Attosecond interferometry of shape resonances in the recoil frame of CF4. Sci. Adv. 7, eabj8121 (2021).
Mazza, T. et al. Determining the polarization state of an extreme ultraviolet free-electron laser beam using atomic circular dichroism. Nat. Commun. 5, 3648 (2014).
Mosert, V. & Bauer, D. Photoelectron spectra with Qprop and t-SURFF. Comput. Phys. Commun. 207, 452–463 (2016).
Fano, U. Propensity rules: an analytical approach. Phys. Rev. A Gen. Phys. 32, 617–618 (1985).
Busto, D. et al. Fano’s propensity rule in angle-resolved attosecond pump-probe photoionization. Phys. Rev. Lett. 123, 133201 (2019).
Kheifets, A. S. Symmetry analysis of the photoelectron continuum in two-photon XUV + IR ionization. Phys. Rev. A 105, 013114 (2022).
Villeneuve, D., Hockett, P., Vrakking, M. & Niikura, H. Coherent imaging of an attosecond electron wave packet. Science 356, 1150–1153 (2017).
Fuchs, J. et al. Time delays from one-photon transitions in the continuum. Optica 7, 154–161 (2020).
Tokunaga, Y. et al. A new class of chiral materials hosting magnetic skyrmions beyond room temperature. Nat. Commun. 6, 7638 (2015).
Rechtsman, M. C. et al. Photonic floquet topological insulators. Nature 496, 196–200 (2013).
Beaulieu, S. et al. Attosecond-resolved photoionization of chiral molecules. Science 358, 1288–1294 (2017).
Zipp, L. J., Natan, A. & Bucksbaum, P. H. Probing electron delays in above-threshold ionization. Optica 1, 361–364 (2014).
Ji, J.-B., Heck, S., Han, M. & Wörner, H. J. Quantitative uncertainty determination of phase retrieval in RABBITT. Opt. Express 29, 27732 (2021).
Meyer, M. et al. Two-color experiments in the gas phase at flash. J. Electron Spectrosc. Related Phenomena 181, 111–115 (2010).
Acknowledgements
M.H. acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement no. 801459 – FP-RESOMUS. This work was supported by ETH Zürich and the Swiss National Science Foundation through projects 200021_172946 and the NCCR-MUST. M.H. acknowledges fruitful discussions with Joss Wiese.
Author information
Authors and Affiliations
Contributions
M.H. performed the experiments with the support of J.-B.J. and T.B. M.H., K. U. and H.J.W. analysed and interpreted the data. Simulations were implemented by M.H. H.J.W. conceived the study and supervised its realization. All authors discussed the results and wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Physics thanks Oleg Tolstikhin and Jean Marcel Ngoko Djiokap for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
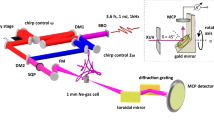
Extended Data Fig. 1 Experimental setup.
See Method section for the detailed description.
Extended Data Fig. 2 Angle-resolved photoelectron-energy spectra from the TDSE simulation in the XUV-only case from the p+, p− and p0 orbitals.
(a-c), Results from the p+, p− and p0 orbitals, respectively. The right panel shows the corresponding electronic transition and the finally populated state, which can explain the calculated photoelectron angular distributions. For example, from the p− orbital the electron will undergo a transition to the d0 state which has three lobes, corresponding to the three maxima in the angular distribution. (d), Energy-integrated photoelectron angular distributions from these three orbitals. The ionization from the p+ orbital is dominant, occupying 70% of the total ionization probability.
Extended Data Fig. 3 Angle-resolved RABBIT traces and the extracted RABBIT phases of SB12 from the TDSE simulation based on the p− and p0 ground-state orbitals.
(a-c), Results from the p− orbital. In this case the m of the main peaks created by the XUV photoionization is zero and thus the continuum electron wave packet has no chirality. Therefore, both the sideband yield and phase don’t depend on the helicity of the probe IR. (d-f), Results from the p0 orbital. In this case the m of the main peaks created by the XUV photoionization is 1, and thus the degree of chirality is less than that from the p+ ground-state orbital. Therefore, the CD effects on the sideband yield and phase are decreased compared to those from the p+ orbital shown in Fig. 2g-i, but the basic structures are not changed.
Extended Data Fig. 4 TDSE simulations on helium atoms.
To illustrate the discrepancy with the previous study [33] on helium atoms, here we performed the TDSE simulations of helium atoms based on the roughly equal parameters. In their study, they used a circularly polarized XUV femtosecond pulse at around 48.4 eV to ionize helium atoms and a circularly polarized IR at 800 nm to probe the electron vortices in the continuum, and they observed the sideband yield in the counter-rotating geometry to be dominant with a CD effect of -6%. To calculate the dichroic RABBIT phase, here we have to use two harmonic orders [H31 (48.05 eV) and H33 (51.15 eV)]. In this single-electron-approximation TDSE simulation, we used the effective potential of helium according to the reference [47]. The electric-field amplitudes of the two harmonics are both equal to 0.0119 a.u., corresponding to an intensity of 1013 W/cm2, and the electric-field amplitude of the IR field is 0.001 a.u.. The spatial step size is reduced to 0.025 a.u. and the temporal step size is reduced to 0.01 a.u.. Other parameters are the same as those described in Methods section. (a, b), Calculated angle-resolved photoelectron energy spectra in co-rotating and counter-rotating geometries, respectively, where the XUV-IR phase delay and the ϕ angle are both integrated over 2π. (c), θ-integrated energy spectra and the corresponding CD spectrum. Note the energy spectra are in the logarithmic scale in order to show the high-order sidebands created by absorbing or releasing two IR photons. The absolute value of our calculated CD of one-IR-photon sidebands is about +7%. Because the electron kinetic energy is much higher than that in our experiments on Argon, the magnitude of the yield CD is decreased. (d, e), Delay- and θ-resolved photoelectron distributions of SB32 in the two geometries. (f), Extracted θ-resolved RABBIT phases from d and e using Fourier transformation. To conclude, the amplitude and phase CDs observed in this study should be qualitatively similar to those of helium atoms.
Extended Data Fig. 5 Retrieval of partial-wave amplitudes and phases from the measured photoelectron interferogram using global fitting.
(a, b), Measured time-resolved photoelectron angular distributions of SB12 in co-rotating and counter-rotating geometries, which are the enlarged plots of Fig. 1f,g, respectively. (c, d), Reconstructed photoelectron interferograms in the two geometries using global fitting of the three-wave interference model based on the p+ ground state.
Source data
Source Data Fig. 1
Source data for Fig. 1e and Fig. 1h.
Source Data Fig. 2
Source data for Fig. 2c, f and i.
Source Data Fig. 4
Source data for Fig. 4.
Source Data Extended Data Fig. 2
Source data for Extended Data Fig. 2d.
Source Data Extended Data Fig. 3
Source data for Extended Data Fig. 3c and f.
Source Data Extended Data Fig. 4
Source Data for the Extended Data Fig. 4c and f.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Han, M., Ji, JB., Balčiūnas, T. et al. Attosecond circular-dichroism chronoscopy of electron vortices. Nat. Phys. 19, 230–236 (2023). https://doi.org/10.1038/s41567-022-01832-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01832-4
This article is cited by
-
Down the RABBIT hole
Nature Physics (2022)