Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Spin–orbital liquid state and liquid–gas metamagnetic transition on a pyrochlore lattice

Nature Physics volume 19, pages 92–98 (2023)Cite this article

Subjects

Abstract

Crystal structures with degenerate electronic orbitals are unstable towards lattice distortions that lift the degeneracy. Although these Jahn–Teller distortions have profound effects on magnetism, they are typically unaffected by the onset of magnetic ordering because of a separation in energy scales. Here we show the contrary case in Pr2Zr2O7, where orbital degeneracy remains down to the millikelvin range due to an interplay between spins and orbitals. Pr2Zr2O7 is a multipolar spin ice with strongly localized 4f electrons in an even-number configuration, giving rise to a non-Kramers doublet that carries transverse quadrupolar and longitudinal dipolar moments. Our study of ultrapure single crystals of Pr2Zr2O7 finds comprehensive evidence for enhanced spin–orbital quantum dynamics of the non-Kramers doublet. This dynamical Jahn–Teller effect is encapsulated by the liquid–gas metamagnetic transition that is characteristic of spin ice being accompanied by strong lattice softening. This behaviour suggests that a spin–orbital liquid state forms on the pyrochlore lattice at low temperatures and low magnetic fields.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Spin–orbital interlocking in the non-Kramers doublet of the multipolar spin ice Pr2Zr2O7 and magnetic-field tuning of its ground state with spin–orbital quantum dynamics.
Fig. 2: First-order liquid–gas metamagnetic transition and strong lattice anomalies in Pr2Zr2O7.
Fig. 3: Low-lying CEP of the liquid–gas metamagnetic transition in Pr2Zr2O7.
Fig. 4: Evidence for magnetodistortive dynamics: dielectric and length-change anomalies and strong lattice softening in Pr2Zr2O7.

Similar content being viewed by others

Data availability

Source data are provided with this paper. All other data that support the plots within this paper are available from the corresponding authors upon reasonable request.

References

  1. Balents, L. Spin liquids in frustrated magnets. Nature 464, 199–208 (2010).

    Article  ADS  Google Scholar 

  2. Gingras, M. J. P. & McClarty, P. A. Quantum spin ice: a search for gapless quantum spin liquids in pyrochlore magnets. Rep. Prog. Phys. 77, 056501 (2014).

    Article  ADS  Google Scholar 

  3. Zhou, Y., Kanoda, K. & Ng, T.-K. Quantum spin liquid states. Rev. Mod. Phys. 89, 025003 (2017).

    Article  ADS  Google Scholar 

  4. Takagi, H., Takayama, T., Jackeli, G., Khaliullin, G. & Nagler, S. E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 1, 264–280 (2019).

    Article  Google Scholar 

  5. Broholm, C. et al. Quantum spin liquids. Science 367, eaay0668 (2020).

    Article  Google Scholar 

  6. Santini, P. et al. Multipolar interactions in f-electron systems: the paradigm of actinide dioxides. Rev. Mod. Phys. 81, 807–863 (2009).

    Article  ADS  Google Scholar 

  7. Paramekanti, A., Maharaj, D. D. & Gaulin, B. D. Octupolar order in d-orbital Mott insulators. Phys. Rev. B 101, 054439 (2020).

    Article  ADS  Google Scholar 

  8. Ross, K. A., Savary, L., Gaulin, B. D. & Balents, L. Quantum excitations in quantum spin ice. Phys. Rev. X 1, 021002 (2011).

    Google Scholar 

  9. Gao, B. et al. Experimental signatures of a three-dimensional quantum spin liquid in effective spin-1/2 Ce2Zr2O7 pyrochlore. Nat. Phys. 15, 1052–1057 (2019).

    Article  Google Scholar 

  10. Sibille, R. et al. A quantum liquid of magnetic octupoles on the pyrochlore lattice. Nat. Phys. 16, 546–552 (2020).

    Article  Google Scholar 

  11. Jahn, H. A. & Teller, E. Stability of polyatomic molecules in degenerate electronic states - I—orbital degeneracy. Proc. R. Soc. Lond. A 161, 220–235 (1937).

    Article  ADS  MATH  Google Scholar 

  12. Kugel, K. I. & Khomskii, D. The Jahn-Teller effect and magnetism: transition metal compounds. Sov. Phys. Usp. 25, 231 (1982).

    Article  ADS  Google Scholar 

  13. Tokura, Y. & Nagaosa, N. Orbital physics in transition-metal oxides. Science 288, 462–468 (2000).

    Article  ADS  Google Scholar 

  14. Feiner, L. F., Oleś, A. M. & Zaanen, J. Quantum melting of magnetic order due to orbital fluctuations. Phys. Rev. Lett. 78, 2799–2802 (1997).

    Article  ADS  Google Scholar 

  15. Khaliullin, G. & Maekawa, S. Orbital liquid in three-dimensional Mott insulator: LaTiO3. Phys. Rev. Lett. 85, 3950–3953 (2000).

    Article  ADS  Google Scholar 

  16. Fichtl, R., Lunkenheimer, P., Hemberger, J., Tsurkan, V. & Loidl, A. Glassy freezing of orbital dynamics in FeCr2S4 and FeSc2S4. J. Non-Cryst. Solids 351, 2793–2797 (2005).

    Article  ADS  Google Scholar 

  17. Chen, G., Balents, L. & Schnyder, A. P. Spin-orbital singlet and quantum critical point on the diamond lattice: FeSc2S4. Phys. Rev. Lett. 102, 096406 (2009).

    Article  ADS  Google Scholar 

  18. Nakatsuji, S. et al. Spin-orbital short-range order on a honeycomb-based lattice. Science 336, 559–563 (2012).

    Article  ADS  Google Scholar 

  19. Corboz, P., Lajkó, M., Läuchli, A. M., Penc, K. & Mila, F. Spin-orbital quantum liquid on the honeycomb lattice. Phys. Rev. X 2, 041013 (2012).

    Google Scholar 

  20. Yu, J.-X. et al. Three Jahn-Teller states of matter in spin-crossover system Mn(taa). Phys. Rev. Lett. 124, 227201 (2020).

    Article  ADS  Google Scholar 

  21. Lee, S., Onoda, S. & Balents, L. Generic quantum spin ice. Phys. Rev. B 86, 104412 (2012).

    Article  ADS  Google Scholar 

  22. Schaffer, R., Bhattacharjee, S. & Kim, Y. B. Spin-orbital liquids in non-Kramers magnets on the kagome lattice. Phys. Rev. B 88, 174405 (2013).

    Article  ADS  Google Scholar 

  23. Rau, J. G. & Gingras, M. J. Frustrated quantum rare-earth pyrochlores. Annu. Rev. Condens. Matter Phys. 10, 357–86 (2019).

    Article  ADS  Google Scholar 

  24. Zhou, H. D. et al. Dynamic spin ice: Pr2Sn2O7. Phys. Rev. Lett. 101, 227204 (2008).

    Article  ADS  Google Scholar 

  25. Machida, Y., Nakatsuji, S., Onoda, S., Tayama, T. & Sakakibara, T. Time-reversal symmetry breaking and spontaneous Hall effect without magnetic dipole order. Nature 463, 210–213 (2010).

    Article  ADS  Google Scholar 

  26. Kimura, K. et al. Quantum fluctuations in spin-ice-like Pr2Zr2O7. Nat. Commun. 4, 1934 (2013).

    Article  ADS  Google Scholar 

  27. Hatnean, M. C. et al. Structural and magnetic properties of single-crystals of the geometrically frustrated zirconium pyrochlore, Pr2Zr2O7. Mater. Res. Express 1, 026109 (2014).

    Article  ADS  Google Scholar 

  28. Petit, S. et al. Antiferroquadrupolar correlations in the quantum spin ice candidate Pr2Zr2O7. Phys. Rev. B 94, 165153 (2016).

    Article  ADS  Google Scholar 

  29. Wen, J.-J. et al. Disordered route to the Coulomb quantum spin liquid: random transverse fields on spin ice in Pr2Zr2O7. Phys. Rev. Lett. 118, 107206 (2017).

    Article  ADS  Google Scholar 

  30. Tokiwa, Y. et al. Discovery of emergent photon and monopoles in a quantum spin liquid. J. Phys. Soc. Jpn 87, 064702 (2018).

    Article  ADS  Google Scholar 

  31. Sibille, R. et al. Candidate quantum spin ice in the pyrochlore Pr2Hf2O7. Phys. Rev. B 94, 024436 (2016).

    Article  ADS  Google Scholar 

  32. Castelnovo, C., Moessner, R. & Sondhi, S. Spin ice, fractionalization, and topological order. Annu. Rev. Condens. Matter Phys. 3, 35–55 (2012).

    Article  Google Scholar 

  33. Castelnovo, C., Moessner, R. & Sondhi, S. L. Magnetic monopoles in spin ice. Nature 451, 42–45 (2008).

    Article  ADS  Google Scholar 

  34. Laurita, N. J. et al. Singlet-triplet excitations and long-range entanglement in the spin-orbital liquid candidate FeSc2S4. Phys. Rev. Lett. 114, 207201 (2015).

    Article  ADS  Google Scholar 

  35. Patri, A. S., Hosoi, M., Lee, S. & Kim, Y. B. Theory of magnetostriction for multipolar quantum spin ice in pyrochlore materials. Phys. Rev. Res. 2, 033015 (2020).

    Article  Google Scholar 

  36. Koohpayeh, S. M., Wen, J.-J., Trump, B. A., Broholm, C. L. & McQueen, T. M. Synthesis, floating zone crystal growth and characterization of the quantum spin ice Pr2Zr2O7 pyrochlore. J. Cryst. Growth 402, 291–298 (2014).

    Article  ADS  Google Scholar 

  37. Martin, N. et al. Disorder and quantum spin ice. Phys. Rev. X 7, 041028 (2017).

    Google Scholar 

  38. Savary, L. & Balents, L. Disorder-induced quantum spin liquid in spin ice pyrochlores. Phys. Rev. Lett. 118, 087203 (2017).

    Article  ADS  Google Scholar 

  39. Benton, O. Instabilities of a U(1) quantum spin liquid in disordered non-Kramers pyrochlores. Phys. Rev. Lett. 121, 037203 (2018).

    Article  ADS  Google Scholar 

  40. Sakakibara, T., Tayama, T., Hiroi, Z., Matsuhira, K. & Takagi, S. Observation of a liquid-gas-type transition in the pyrochlore spin ice compound Dy2Ti2O7 in a magnetic field. Phys. Rev. Lett. 90, 207205 (2003).

    Article  ADS  Google Scholar 

  41. Bojesen, T. A. & Onoda, S. Quantum spin ice under a [111] magnetic field: from pyrochlore to kagome. Phys. Rev. Lett. 119, 227204 (2017).

    Article  ADS  Google Scholar 

  42. Dzyaloshinsky, I. A thermodynamic theory of ‘weak’ ferromagnetism of antiferromagnetics. J. Phys. Chem. Solids 4, 241–255 (1958).

    Article  ADS  Google Scholar 

  43. Moriya, T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 120, 91–98 (1960).

    Article  ADS  Google Scholar 

  44. Sarkar, A. & Mukhopadhyay, S. Dynamics of electrically polarized magnetic monopoles in spin ice. Phys. Rev. B 90, 165129 (2014).

    Article  ADS  Google Scholar 

  45. Lin, L. et al. Experimental observation of magnetoelectricity in spin ice Dy2Ti2O7. New J. Phys. 17, 123018 (2015).

    Article  ADS  Google Scholar 

  46. Khomskii, D. Electric dipoles on magnetic monopoles in spin ice. Nat. Commun. 3, 904 (2012).

    Article  ADS  Google Scholar 

  47. Saito, M., Higashinaka, R. & Maeno, Y. Magnetodielectric response of the spin-ice Dy2Ti2O7. Phys. Rev. B 72, 144422 (2005).

    Article  ADS  Google Scholar 

  48. Bhattacharjee, S. et al. Acoustic signatures of the phases and phase transitions in Yb2Ti2O7. Phys. Rev. B 93, 144412 (2016).

    Article  ADS  Google Scholar 

  49. Bhattacharjee, S. et al. Interplay of spin and lattice degrees of freedom in the frustrated antiferromagnet CdCr2O4: high-field and temperature-induced anomalies of the elastic constants. Phys. Rev. B 83, 184421 (2011).

    Article  ADS  Google Scholar 

  50. Erfanifam, S. et al. Ultrasonic investigations of the spin ices Dy2Ti2O7 and Ho2Ti2O7 in and out of equilibrium. Phys. Rev. B 90, 064409 (2014).

    Article  ADS  Google Scholar 

  51. Banerjee, A., Isakov, S. V., Damle, K. & Kim, Y. B. Unusual liquid state of hard-core bosons on the pyrochlore lattice. Phys. Rev. Lett. 100, 047208 (2008).

    Article  ADS  Google Scholar 

  52. Benton, O., Sikora, O. & Shannon, N. Seeing the light: experimental signatures of emergent electromagnetism in a quantum spin ice. Phys. Rev. B 86, 075154 (2012).

    Article  ADS  Google Scholar 

  53. Seth, A., Bhattacharjee, S. & Moessner, R. Probing emergent QED in quantum spin ice via Raman scattering of phonons: shallow inelastic scattering and pair production. Phys. Rev. B 106, 054507 (2022).

  54. Sheldrick, G. M. A short history of SHELX. Acta Cryst. A64, 112–122 (2008).

    Article  MATH  Google Scholar 

  55. Burla, M. C. et al. SIR2004: an improved tool for crystal structure determination and refinement. J. Appl. Cryst. 38, 381–388 (2005).

    Article  ADS  Google Scholar 

  56. Tabira, Y., Withers, R. L., Minervini, L. & Grimes, R. W. Systematic structural change in selected rare earth oxide pyrochlores as determined by wide-angle CBED and a comparison with the results of atomistic computer simulation. J. Solid State Chem. 153, 16–25 (2000).

    Article  ADS  Google Scholar 

  57. Sakata, M. & Sato, M. Accurate structure analysis by the maximum-entropy method. Acta Cryst. A46, 263–270 (1990).

    Article  Google Scholar 

  58. Küchler, R., Bauer, T., Brando, M. & Steglich, F. A compact and miniaturized high resolution capacitance dilatometer for measuring thermal expansion and magnetostriction. Rev. Sci. Instrum. 83, 095102 (2012).

    Article  ADS  Google Scholar 

  59. Sakakibara, T., Mitamura, H., Tayama, T. & Amitsuka, H. Faraday force magnetometer for high-sensitivity magnetization measurements at very low temperatures and high fields. Jpn. J. Appl. Phys. 33, 5067–5072 (1994).

    Article  ADS  Google Scholar 

  60. Aharoni, A. Demagnetizing factors for rectangular ferromagnetic prisms. J. Appl. Phys. 83, 3432–3434 (1998).

    Article  ADS  Google Scholar 

  61. Kimura, K. & Nakatsuji, S. Magnetic and thermal properties of the single crystalline Pr2Zr2O7 in a [111] field. JPS Conf. Proc. 3, 014027 (2014).

    Google Scholar 

  62. Van Vleck, J. H. The theory of electric and magnetic susceptibilities. Nature 130, 490–491 (1932).

    Article  MATH  Google Scholar 

  63. Nakanishi, Y. et al. Elastic properties of the rare-earth dititanates R2Ti2O7 (R = Tb, Dy, and Ho). Phys. Rev. B 83, 184434 (2011).

    Article  ADS  Google Scholar 

  64. Kondo, J. Internal magnetic field in rare earth metals. J. Phys. Soc. Jpn 16, 1690–1691 (1961).

    Article  ADS  Google Scholar 

  65. Mirebeau, I. et al. Ordered spin ice state and magnetic fluctuations in Tb2Sn2O7. Phys. Rev. Lett. 94, 246402 (2005).

    Article  ADS  Google Scholar 

  66. Xu, Y. et al. Importance of dynamic lattice effects for crystal field excitations in the quantum spin ice candidate Pr2Zr2O7. Phys. Rev. B 104, 075125 (2021).

    Article  ADS  Google Scholar 

  67. Xu, Y. et al. Phonon spectrum of Pr2Zr2O7 and Pr2Ir2O7 as evidence of coupling of the lattice with electronic and magnetic degrees of freedom. Phys. Rev. B 105, 075137 (2022).

    Article  ADS  Google Scholar 

  68. Matsuhira, K. et al. Spin freezing in the pyrochlore antiferromagnet Pr2Zr2O7. J. Phys. Conf. Ser. 145, 012031 (2009).

    Article  Google Scholar 

Download references

Acknowledgements

We thank Y. Motome, Y. Kato, T. A. Bojeson, S. Nakamura, N. Kawashima, A. A. Nugroho, H. Kusunose and S. Onoda for helpful discussion. This work is partially supported by JST-CREST (JPMJCR18T3), JST-PRESTO (JPMJPR15N5) and by Grants-in-Aid for Scientific Research (JP19H00650 and 20K03829) from the Japan Society for the Promotion of Science (JSPS). Institute for Quantum Matter, an Energy Frontier Research Center, was funded by the Department of Energy, Office of Science, Basic Energy Sciences, under award no. DE-SC0019331. The use of the facilities of the Materials Design and Characterization Laboratory at the ISSP, The University of Tokyo, is acknowledged. S.B. acknowledges funding from a Max Planck Partner group Grant at ICTS; hospitality of visitors program at the Max Planck Institute for the Physics of Complex Systems, Dresden; and ISSP, The University of Tokyo; Science and Engineering Research Board—Department of Science and Technology (India) for funding through project grant no. ECR/2017/000504 and the support of the Department of Atomic Energy, Government of India, under project nos. 12-R&D-TFR-5.10-1100 and RTI4001. We acknowledge support of the HLD at HZDR, member of the European Magnetic Field Laboratory (EMFL). This work was in part supported by the Deutsche Forschungsgemeinschaft under grants SFB 1143 (Project ID 247310070) and the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter—ct.qmat (EXC 2147, Project ID 390858490).

Author information

Author notes

  1. These authors contributed equally: Nan Tang, Yulia Gritsenko, Kenta Kimura.

Authors and Affiliations

  1. Department of Physics, University of Tokyo, Tokyo, Japan

    Nan Tang, Akito Sakai, Mingxuan Fu & Satoru Nakatsuji

  2. Institute for Solid State Physics (ISSP), University of Tokyo, Kashiwa, Japan

    Nan Tang, Kenta Kimura, Akito Sakai, Mingxuan Fu, Hikaru Takeda, Huiyuan Man, Yosuke Matsumoto, Yasuyuki Shimura, Masashi Takigawa, Toshiro Sakakibara & Satoru Nakatsuji

  3. Institut für Festkörper- und Materialphysik, Technische Universität Dresden, Dresden, Germany

    Yulia Gritsenko & Joachim Wosnitza

  4. Hochfeld-Magnetlabor Dresden and Würzburg-Dresden Cluster of Excellence ct.qmat, Helmholtz-Zentrum Dresden-Rossendorf, Dresden, Germany

    Yulia Gritsenko, Sergei Zherlitsyn & Joachim Wosnitza

  5. Department of Advanced Materials Science, University of Tokyo, Kashiwa, Japan

    Kenta Kimura

  6. International Centre for Theoretical Sciences, Tata Institute of Fundamental Research, Bengaluru, India

    Subhro Bhattacharjee

  7. Institute for Quantum Matter and Department of Physics and Astronomy, Johns Hopkins University, Baltimore, MD, USA

    Huiyuan Man, Jiajia Wen, Collin Broholm & Satoru Nakatsuji

  8. Department of Applied Physics, Nagoya University, Nagoya, Japan

    Kento Sugawara & Hiroshi Sawa

  9. Synchrotron Radiation Research Center, National Institutes for Quantum Science and Technology, Hyogo, Japan

    Kento Sugawara

  10. Max Planck Institute for Solid State Research, Stuttgart, Germany

    Yosuke Matsumoto

  11. Department of Quantum Matter, Hiroshima University, Hiroshima, Japan

    Yasuyuki Shimura

  12. Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Stanford, CA, USA

    Jiajia Wen

  13. Max-Planck-Institut für Physik komplexer Systeme, Dresden, Germany

    Roderich Moessner

  14. Trans-Scale Quantum Science Institute, University of Tokyo, Tokyo, Japan

    Satoru Nakatsuji

  15. Toyota Physical and Chemical Research Institute, Aichi, Japan

    Masashi Takigawa

  16. Institute of Materials Structure Research, KEK, Ibaragi, Japan

    Masashi Takigawa

  17. Canadian Institute for Advanced Research, Toronto, ON, Canada

    Satoru Nakatsuji

Authors
  1. Nan Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yulia Gritsenko
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kenta Kimura
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Subhro Bhattacharjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Akito Sakai
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Mingxuan Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Hikaru Takeda
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Huiyuan Man
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Kento Sugawara
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Yosuke Matsumoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Yasuyuki Shimura
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Jiajia Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. Collin Broholm
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. Hiroshi Sawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. Masashi Takigawa
    View author publications

    You can also search for this author in PubMed Google Scholar

  16. Toshiro Sakakibara
    View author publications

    You can also search for this author in PubMed Google Scholar

  17. Sergei Zherlitsyn
    View author publications

    You can also search for this author in PubMed Google Scholar

  18. Joachim Wosnitza
    View author publications

    You can also search for this author in PubMed Google Scholar

  19. Roderich Moessner
    View author publications

    You can also search for this author in PubMed Google Scholar

  20. Satoru Nakatsuji
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.N. conceived the project and planned the experiments. S.N., J.Wosnitza. and C.B. supervised the experiments. K.K. and S.N. grew the single crystals. N.T. and A.S. performed the thermal expansion/magnetostriction measurements and N.T., M.F. and A.S. analysed the data. Y.G. and S.Z. performed the ultrasound measurements and analysed the data. K.K. and Y.M. performed the dielectric measurements and K.K. analysed the data. Y.M., K.K. and J.Wen. performed the specific heat measurements and N.T. and Y.M. analysed the data. T.S., Y.S., K.K. and N.T. performed the magnetization measurements, and K.K. and N.T. analysed the data. K.S. and H.S. collected and analysed the synchrotron X-ray diffraction data. H.T. and M.T. carried out the NQR measurements and analysed the data. S.B. and R.M. wrote the theoretical notes in the Supplementary Information. S.N., N.T., S.B., M.F., R.M., Y.G. and K.K. wrote the main text and prepared the figures. N.T., M.F., K.K., S.N., Y.G. and H.M. wrote the Methods section. All the authors discussed the results and commented on the manuscript.

Corresponding author

Correspondence to Satoru Nakatsuji.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

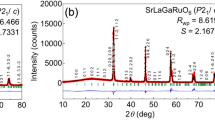
Extended Data Fig. 1 Crystal structure analysis by single crystal synchrotron X-ray diffraction of Pr2Zr2O7.

Contour plot of the reliability factor R1 as a function of x and y in (Pr1−xZrx)2(Zr1−yPry)2O7 is shown.

Source data

Extended Data Fig. 2 Sample quality dependence of physical properties of Pr2Zr2O7.

a, Magnetic field (B) dependence of the magnetization measured along the crystallographic [111] axis and its B-derivative for three samples (sample #1, sample #2, and sample #3) taken from different single crystalline rods (rod 1, rod 2, and rod 3). Measurement temperatures are also indicated. b, NQR spectra and Lorentzian fits for the three samples measured at 4.2 K. Sample #1 and sample #2 that exhibit the metamagnetism produce sharper NQR spectra (smaller FWHM values as shown in each panel) than sample #3 that does not show any metamagnetism. c, Temperature (T) dependence of the magnetic specific heat CM for three samples of different quality. CM is obtained by subtracting CL, CCEF and CN from CP (See Extended Data Fig. 6). The data of sample #3 is taken from Ref. 26. The inset shows CM with respect to T − Thump(K) so that the hump is centred at 0 K. Thump is ∼ 1.4 K, ∼ 1.7 K, ∼ 2.6 K for sample #1, #2, #3, respectively. It is easily seen that the best sample exhibits the narrowest hump structure.

Source data

Extended Data Fig. 3 Strongly anisotropic magnetization curve of Pr2Zr2O7.

a, Magnetization (M) measured under field (B) along the crystallographic [100], [110], and [111] axes at T = 65(5) mK. Dashed lines denote the saturation M along each axis estimated using the effective moment (μeff ≈ 2.5 μB) deduced from the Curie-Weiss fit. The magnetization curve for Dy2Ti2O7 at 50 mK, adapted from Ref. 40, is also shown. M and B for Dy2Ti2O7 are scaled to those for Pr2Zr2O7 with respect to the value of μeff(∼ 2.5 μB for Pr3+ and ∼ 10 μB for Dy3+) and the metamagnetic field Bc (∼ 2.2 T for Pr2Zr2O7 and ∼ 0.9 T for Dy2Ti2O7), respectively. b, B dependence of the field derivative of M in (a).

Source data

Extended Data Fig. 4 Van Vleck and other contributions to magnetization M of Pr2Zr2O7.

M (left axis) and its susceptibility dM /dB (right axis) of Pr2Zr2O7 obtained at T = 60 mK under B ‖ [111]. The Van Vleck term (red dashed line), calculated from the CEF scheme obtained from the neutron scattering results in Ref. 26, is subtracted from the experimental M (left axis, dark blue circles). The result is shown in light blue circles. Magnetic susceptibility dM /dB (right axis) corresponds to the subtracted data.

Source data

Extended Data Fig. 5 Splitting of non-Kramers ground doublet due to the linear coupling between transverse quadrupolar component Sx and elastic strain εx in magnetic field Hz.

a, Quadrupolar-strain coupling lifts the degeneracy of the ground state doublet by opening a gap of ∆. In this case, |Sx+〉state is energetically more favorable and physically selected. b, Evolution of the non-Kramers doublet with increasing elastic strain εx by distorting D3d CEF under a fixed strength of magnetic field Hz. |Sx+〉state is stretched along the local x direction and hence, energetically more favorable in this case. Each three wavefunctions of |Sx+〉(top) and |Sx−〉(bottom) states correspond to the doublet gap of ∆ ∼ 0 K (Left), ∼ 1.3 K (middle), ∼ 5.4 K (Right). It is important to note that in real crystals of Pr2Zr2O7, there is no static strain or internal magnetic field. These pictures are only for an illustrative purpose.

Extended Data Fig. 6 Temperature (T) dependence of the specific heat for three Pr2Zr2O7 samples of different quality.

a, b, c, T dependence of the magnetic and nuclear part of the specific heat CMN (open circles) for three Pr2Zr2O7 samples of different quality after subtracting lattice (dull yellow line) and CEF (dark blue line) contributions from the measured specific heat Cp (open rhombus) in zero field (see Methods for details). CMN is defined as CMN ≡ CM + CN = CP − CL − CCEF. CM is the magnetic specific heat (solid circle). CN is the Schottky-like specific heat that fits CMN below T ≈ 0.2 K. A refined estimate CM = CMN − CN was obtained by subtracting a scaled nuclear Schottky-like anomaly (cyan line). d, e, f, T dependence of the corresponding entropies obtained through integration from absolute zero. The fitting results CN is used for the experimentally inaccessible temperature range in order to perform the integration. Open circles denote the magnetic and nuclear entropy SMN, while the solid circles denote the magnetic entropy SM. The three dashed black lines denote ∆S for a spin ice system, a spin ice system with a nuclear contribution of I = 5/2, and a two-level electronic system with a nuclear contribution of I = 5/2, respectively.

Source data

Extended Data Fig. 7 Temperature (T) dependence of the magnetization M and the thermal expansion ∆L/L0 at high fields for Pr2Zr2O7.

a, b, T dependence of (a) M and (b) longitudinal ∆L/L0 at B = 3 and 5 T, where B is applied along the [111] direction. ∆L/L0 has a constant shift along the y axis for clarity.

Source data

Extended Data Table 1

Crystallographic parameters for Pr2Zr2O7 at 20 K.

Extended Data Table 2

Atomic positions for Pr2Zr2O7 at 20 K.

Extended Data Table 3

Sample dependence of Curie-Weiss temperature Tθ and metamagnetic behaviour in Pr2Zr2O7.

Supplementary information

Supplementary Information

Supplementary Sections 1–7, Fig. 1, Table 1 and references.

Source data

Source Data Fig. 1

Statistical source data.

Source Data Fig. 2

Statistical source data.

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Extended Data Fig. 1

Statistical source data.

Source Data Extended Data Fig. 2

Statistical source data.

Source Data Extended Data Fig. 3

Statistical source data.

Source Data Extended Data Fig. 4

Statistical source data.

Source Data Extended Data Fig. 6

Statistical source data.

Source Data Extended Data Fig. 7

Statistical source data.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, N., Gritsenko, Y., Kimura, K. et al. Spin–orbital liquid state and liquid–gas metamagnetic transition on a pyrochlore lattice. Nat. Phys. 19, 92–98 (2023). https://doi.org/10.1038/s41567-022-01816-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01816-4

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing