Measurement of anti-³He nuclei absorption in matter and impact on their propagation in the Galaxy

Abstract

In our Galaxy, light antinuclei composed of antiprotons and antineutrons can be produced through high-energy cosmic-ray collisions with the interstellar medium or could also originate from the annihilation of dark-matter particles that have not yet been discovered. On Earth, the only way to produce and study antinuclei with high precision is to create them at high-energy particle accelerators. Although the properties of elementary antiparticles have been studied in detail, the knowledge of the interaction of light antinuclei with matter is limited. We determine the disappearance probability of ${}^{3}\overline{{{{\rm{He}}}}}$ when it encounters matter particles and annihilates or disintegrates within the ALICE detector at the Large Hadron Collider. We extract the inelastic interaction cross section, which is then used as an input to the calculations of the transparency of our Galaxy to the propagation of ${}^{3}\overline{{{{\rm{He}}}}}$ stemming from dark-matter annihilation and cosmic-ray interactions within the interstellar medium. For a specific dark-matter profile, we estimate a transparency of about 50%, whereas it varies with increasing ${}^{3}\overline{{{{\rm{He}}}}}$ momentum from 25% to 90% for cosmic-ray sources. The results indicate that ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei can travel long distances in the Galaxy, and can be used to study cosmic-ray interactions and dark-matter annihilation.

Main

There are no natural forms of antinuclei on Earth, but we know they exist because of fundamental symmetries in particle physics and their observation in interactions of high-energy accelerated beams. Light antinuclei, objects composed of antiprotons ($\overline{{{{\rm{p}}}}}$) and antineutrons ($\overline{{{{\rm{n}}}}}$), such as $\overline{{{{\rm{d}}}}}$ ($\overline{{{{\rm{pn}}}}}$), ${}^{3}\overline{{{{\rm{He}}}}}$ ($\overline{{{{\rm{ppn}}}}}$) and ${}^{4}\overline{{{{\rm{He}}}}}$ ($\overline{{{{\rm{ppnn}}}}}$), have been produced and studied at various accelerator facilities^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18}, including precision measurements of the mass difference between nuclei and antinuclei^19,20. The interest in the properties of such objects is manifold. From the nuclear physics perspective, the production mechanism and interactions of antinuclei can elucidate the detailed features of the strong interaction that binds nucleons into nuclei²¹. From the astrophysical standpoint, natural sources of antinuclei may include the annihilation of dark-matter (DM) particles such as weakly interacting massive particles²² and other exotic sources such as antistars^23,24. DM constitutes about 27% of the total energy density budget within our Universe²⁵. This is demonstrated by the measurement of the fine structure of the cosmic microwave background^26,27, gravitational lensing of galaxy clusters²⁸ and the rotational curves of some galaxies²³. Another possible source of antinuclei in our Universe is high-energy cosmic-ray collisions with atoms in the interstellar medium.

The observation of antinuclei such as ${}^{3}\overline{{{{\rm{He}}}}}$ is one of the most promising signatures of DM annihilation of weakly interacting massive particles^{22,29,30,31,32}. The kinetic-energy distribution of antinuclei produced in DM annihilation peaks at low kinetic energies (E_kin per nucleon ≲ 1 GeV A^–1) for most assumptions of DM mass²². In contrast, for antinuclei originating from cosmic-ray interactions, the spectrum peaks at much larger E_kin per nucleon (~10 GeV A^–1). Thus, the low-energy region is almost free of background for DM searches.

To calculate the expected flux of antinuclei near Earth, one needs to precisely know the antinucleus formation and annihilation probabilities in the Galaxy. The formation probability of light antinuclei (up to mass number A = 4) is currently studied at accelerators. By now, several models successfully describe light-antinuclei production yields^{33,34,35,36,37}. Such models are based on either the statistical hadronization^12,38,39,40 or coalescence approach^{41,42,43,44,45}.

Another crucial aspect in the search of antinuclei in our Galaxy is the knowledge of their disappearance probability when they encounter matter and annihilate or disintegrate. Antinuclei generated in our Galaxy may travel thousands of light years⁴⁶ before reaching the Earth and being detected. The journey of antinuclei through the Galaxy can be modelled by propagation codes, which incorporate the initial distribution of antinucleus sources, interstellar gas distribution in the Galaxy, elastic scatterings and inelastic hadronic interactions with the interstellar medium. The antinucleus flux in the Solar System is further modulated by solar magnetic fields. During the entire journey, antinuclei can encounter matter and disappear. The disappearance probability is quantified through the inelastic cross section. It is normally studied employing particle beams of interest impinging on targets of known composition and thickness, but antinuclei beams are very challenging to obtain. Today, the Large Hadron Collider (LHC) is the best facility to study nuclear antimatter since its high energies allow one to produce, on average, as many nuclei as antinuclei in proton–proton (pp) and lead–lead (Pb–Pb) collisions^12,47. The detector material can serve as the target and the disappearance probability can be experimentally determined⁴⁸.

This work presents the measurement of the ${}^{3}\overline{{{{\rm{He}}}}}$ inelastic cross section σ_inel(³$\overline{{{{\rm{He}}}}}$), obtained using data from the ALICE experiment. These results are used in model calculations to assess the effect of the disappearance of antinuclei during their propagation through our Galaxy. The associated uncertainties are estimated based on experimental data. The transparency of our Galaxy to the propagation of ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei stemming from a specific DM source and from interactions of high-energy cosmic rays with the interstellar medium is determined, providing one of the necessary constraints for the study of antinuclei in space.

Determination of the inelastic cross section

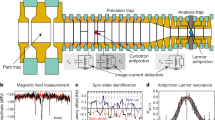
The measurement of the inelastic cross sections under controlled conditions requires a beam with a well-defined momentum and a target whose material and its spatial distribution are well known. Since no ${}^{3}\overline{{{{\rm{He}}}}}$ beams are available, we exploit the antimatter production at the LHC and the excellent identification and momentum determination for ${}^{3}\overline{{{{\rm{He}}}}}$ in ALICE as an equivalent setup. In our study, the ALICE detector itself serves as the target for inelastic processes. A detailed description of the detector and its performance is available elsewhere^49,50. Here, serving as probes, ${}^{3}\overline{{{{\rm{He}}}}}$ and ³He nuclei are produced in pp and Pb–Pb collisions. At LHC high energies, ${}^{3}\overline{{{{\rm{He}}}}}$ and ³He are produced in the same amounts on average. The primordial ratio can be derived from precise antiproton-to-proton measurements^47,51 and in pp collisions at the centre-of-mass energy of $\sqrt{s}$ = 13 TeV corresponds to 0.994 ± 0.045. The ALICE subdetectors that are considered as targets are the inner tracking system (ITS), the time projection chamber (TPC) and the transition radiation detector (TRD). A schematic of the ALICE detector is shown in Fig. 1a. The material composition of the three subdetectors is diverse. The detailed knowledge of the detector geometry and composition^50,52 (see the Supplemental Material of ref. ⁴⁸ for a cumulative distribution of the material in the ALICE apparatus) enables the determination of the effective target material for this layered configuration (Methods). Here σ_inel(³$\overline{{{{\rm{He}}}}}$) can be estimated for three effective targets. The first one is characterized by the average material of the ITS + TPC systems (with averaged atomic mass and charge numbers of 〈A〉 = 17.4 and 〈Z〉 = 8.5, respectively), the second one corresponds to the ITS + TPC + TRD systems (〈A〉 = 31.8 and 〈Z〉 = 14.8)⁴⁸ and the third one corresponds to the TRD system only (〈A〉 = 34.7 and 〈Z〉 = 16.1). The values are obtained by weighting the contribution from different materials with their density times the length crossed by particles.

Fig. 1: Description of the steps followed for the extraction of σ_inel(³$\overline{{{{\rm{He}}}}}$).

a, Schematic of the ALICE detectors at midrapidity in the plane perpendicular to the beam axis, with the collision point located in the middle; the ITS, TPC, TRD and TOF detectors are shown in green, blue, yellow and orange, respectively. A ${}^{3}\overline{{{{\rm{He}}}}}$ that annihilates in the TPC gas is shown in red, and a ³He that does not undergo an inelastic reaction and reaches the TOF detector is shown in blue; the dashed curves represent charged (anti)particles produced in the ${}^{3}\overline{{{{\rm{He}}}}}$ annihilation. b, Identification of (anti)nuclei by means of their specific energy loss dE/dx and momentum measurement in the TPC. The red points show all the (anti)³He nuclei reconstructed with the TPC detector, and the blue points correspond to (anti)³He with TOF information; other (anti)particles are shown in black. c, Experimental results for the raw ratio of ${}^{3}\overline{{{{\rm{He}}}}}$ to ³He in pp collisions at $\sqrt{s}$ = 13 TeV as a function of rigidity. The vertical lines and boxes represent statistical and systematic uncertainties in terms of standard deviations, respectively. The black and red lines show the results from the MC simulations with varied σ_inel(³$\overline{{{{\rm{He}}}}}$). d, Experimental ratio of ${}^{3}\overline{{{{\rm{He}}}}}$ with TOF information over ${}^{3}\overline{{{{\rm{He}}}}}$ reconstructed in the TPC in the 10% most central Pb–Pb collisions at $\sqrt{{s}_{{{{\rm{NN}}}}}}$ = 5.02 TeV as a function of rigidity. The black and red lines show the results from the MC simulations with varied σ_inel(³$\overline{{{{\rm{He}}}}}$) values. e, Raw ratio of ${}^{3}\overline{{{{\rm{He}}}}}$ to ³He in a particular rigidity interval as a function of σ_inel(³$\overline{{{{\rm{He}}}}}$) for 〈A〉 = 17.4. The fit to the results from MC simulations (black points) shows the dependence of the observable on σ_inel(³$\overline{{{{\rm{He}}}}}$) according to the Lambert–Beer formula. The horizontal dashed blue lines show the central value and 1σ uncertainties for the measured observable and their intersection with the Lambert–Beer function determines σ_inel(³$\overline{{{{\rm{He}}}}}$) limits (yellow lines). f, Extraction of σ_inel(³$\overline{{{{\rm{He}}}}}$) for 〈A〉 = 34.7 analogous to the data in e, with σ_inel(³$\overline{{{{\rm{He}}}}}$) limits shown as the magenta lines.

Figure 1 shows a schematic of the analysis steps necessary to extract σ_inel(³$\overline{{{{\rm{He}}}}}$). Figure 1a shows the ${}^{3}\overline{{{{\rm{He}}}}}$ and ³He tracks crossing the ALICE detector, with the annihilation occurring for ${}^{3}\overline{{{{\rm{He}}}}}$. The momentum p is measured via the determination of the track trajectory and curvature radius in the ALICE magnetic field (B = 0.5 T). Here ${}^{3}\overline{{{{\rm{He}}}}}$ and ³He are first identified when they reach the TPC by the measurement of their specific energy loss (dE/dx) in the detector gas. The excellent separation power of this measurement is shown in Fig. 1b, where dE/dx is presented as a function of particle rigidity (p/z) and z denotes the charge of the particle crossing the TPC in units of electron charge. Here the red dots represent all the nuclei that are reconstructed in the TPC, whereas the blue dots show the nuclei that survive up to the time-of-flight (TOF) detector where they are matched to a TOF hit. A more detailed description of the employed particle identification methods can be found in Methods.

We use two methods to evaluate σ_inel(³$\overline{{{{\rm{He}}}}}$). The first method, applied to the pp data sample at $\sqrt{s}$ = 13 TeV, relies on the comparison of the measured ${}^{3}\overline{{{{\rm{He}}}}}$ and ³He yields (antibaryon-to-baryon method). In this case, the experimental observable is constituted by the reconstructed ${}^{3}\overline{{{{\rm{He}}}}}$/³He ratio analogously to the method used elsewhere⁴⁸ for (anti)deuterons. The inelastic process that takes place in the ITS, TPC or TRD material manifests itself by the fact that fewer ${}^{3}\overline{{{{\rm{He}}}}}$ than ³He candidates are detected (Fig. 1c). Both destructive and non-destructive inelastic processes contribute to this effect. Here the full circular blue symbols show the momentum-dependent ${}^{3}\overline{{{{\rm{He}}}}}$/³He ratio measured in pp collisions as a function of the particle rigidity reconstructed at the primary vertex (p_primary/∣z∣). The discontinuity of the ${}^{3}\overline{{{{\rm{He}}}}}$/³He ratio observed at p_primary/∣z∣ = 1 GeV c^–1 is due to the additional requirement of a hit in the TOF detector for momenta above this value. This ratio can also be evaluated by means of a full-scale Monte Carlo (MC) simulation of antinuclei and nuclei traversing the ALICE detector.

The measured observables are compared in each momentum interval with simulations where σ_inel(³$\overline{{{{\rm{He}}}}}$) is varied to obtain the inelastic cross sections. We performed several full-scale simulations with variations in σ_inel(³$\overline{{{{\rm{He}}}}}$) with respect to the standard parameterization implemented in the Geant4 package^53,54 (Fig. 1c). Figure 1e presents the simulated ratio as a function of σ_inel(³$\overline{{{{\rm{He}}}}}$) parameterized using the Lambert–Beer law⁵⁵. For each momentum interval, the uncertainties of σ_inel(³$\overline{{{{\rm{He}}}}}$) are obtained by requiring an agreement at ±1σ with the measured observables, where σ represents the total experimental uncertainty (statistical and systematic uncertainties added in quadrature).

The second method, employed in the Pb–Pb data analysis at a centre-of-mass energy per nucleon pair $\sqrt{{s}_{{{{\rm{NN}}}}}}$ = 5.02 TeV, measures the disappearance of ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei in the TRD detector only (TOF-to-TPC method). The ratio of ${}^{3}\overline{{{{\rm{He}}}}}$ with TOF information to all the ${}^{3}\overline{{{{\rm{He}}}}}$ candidates is considered as an experimental observable. Figure 1d shows the momentum-dependent ratio of ${}^{3}\overline{{{{\rm{He}}}}}$ with a reconstructed TOF hit to all the ${}^{3}\overline{{{{\rm{He}}}}}$ candidates extracted from Pb–Pb collisions. As with the first method, this observable is also evaluated by means of a full-scale MC Geant4 simulation assuming different σ_inel(³$\overline{{{{\rm{He}}}}}$) values. Figure 1f shows the extraction of σ_inel(³$\overline{{{{\rm{He}}}}}$) and its related uncertainties for one rigidity interval following the same procedure as the one used in the first method.

The final results are shown in Fig. 2. Figure 2 (left) shows the σ_inel(³$\overline{{{{\rm{He}}}}}$) results from the pp data analysis with the yellow boxes representing the ±1σ uncertainty intervals. In Fig. 2 (right), the histogram with the magenta error boxes shows σ_inel(³$\overline{{{{\rm{He}}}}}$) extracted from the Pb–Pb data analysis. The results are shown as a function of momentum p at which the inelastic interaction occurs. Due to continuous energy loss inside the detector material, this momentum is lower than p_primary reconstructed at the primary vertex (Methods). The antibaryon-to-baryon ratio method is applied in the pp data analysis, enabling the measurement of σ_inel(³$\overline{{{{\rm{He}}}}}$) down to a low momentum. The copious background makes this method inapplicable in Pb–Pb collisions below p = 1.5 GeV c^–1 (Methods). The TOF-to-TPC method is unavailable in this momentum range since ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei do not reach the TOF due to the large energy loss and bending within the magnetic field. On the other hand, for momentum values larger than p = 1.5 GeV c^–1, the yield of produced ${}^{3}\overline{{{{\rm{He}}}}}$ is substantially larger in Pb–Pb collisions, thus leading to higher statistical precision for this colliding system using the TOF-to-TPC method. The evaluation of systematic uncertainties is described in Methods. These two independent analysis methods, therefore, provide access to slightly different momentum ranges and to different 〈A〉 values and deliver consistent results in the common momentum region.

Fig. 2: Results for σ_inel(³$\overline{{{{\rm{He}}}}}$) as a function of ${}^{3}\overline{{{{\rm{He}}}}}$ momentum.

Results obtained from pp collisions at $\sqrt{s}$ = 13 TeV (left); results from the 10% most central Pb–Pb collisions at $\sqrt{{s}_{{{{\rm{NN}}}}}}$ = 5.02 TeV (right). The curves represent the Geant4 cross sections corresponding to the effective material probed by the different analyses. The arrow on the left plot shows the 95% confidence limit on σ_inel(³$\overline{{{{\rm{He}}}}}$) for 〈A〉 = 17.4. The different values of 〈A〉 correspond to the three different effective targets (see the main text for details). All the indicated uncertainties represent standard deviations.

The cross section used by Geant4 for the average mass number 〈A〉 of the material is shown by the dashed lines in Fig. 2. It is obtained from a Glauber model parameterization⁵⁴ of the collisions of ${}^{3}\overline{{{{\rm{He}}}}}$ with the target nuclei in which the antinucleon–nucleon cross-section value is taken from the measured $\overline{{{{\rm{p}}}}}$p collisions⁵⁶. Agreement with the experimental σ_inel(³$\overline{{{{\rm{He}}}}}$) value is observed within two standard deviations in the studied momentum range.

Propagation of antinuclei in the interstellar medium

To estimate the transparency of our Galaxy to ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei, we consider two examples of ${}^{3}\overline{{{{\rm{He}}}}}$ production sources. Results from another work⁵⁷ are used as the input for the production cross section of ${}^{3}\overline{{{{\rm{He}}}}}$ from cosmic-ray collisions with the interstellar medium. As a DM source of ${}^{3}\overline{{{{\rm{He}}}}}$, we consider weakly interacting massive particle candidates with a mass of 100 GeV c^–2 annihilating into W⁺W⁻ pairs followed by hadronization into (anti)nuclei²⁹. In both cases, the yields of produced ${}^{3}\overline{{{{\rm{He}}}}}$ are determined by employing the coalescence model that builds antinuclei from antineutrons and antiprotons that are close-by in the phase space^12,41,42. More details about the cosmic-ray and DM sources are discussed in Methods. Additional ${}^{3}\overline{{{{\rm{He}}}}}$ sources such as supernovae remnants⁵⁸, antistars^23,24 and primordial black holes^59,60,61 have not been included in this work.

We consider the DM density distribution in our Galaxy according to the Navarro–Frenk–White profile⁶² (Fig. 3, top), where a schematic of the ${}^{3}\overline{{{{\rm{He}}}}}$ production from cosmic-ray interaction with the interstellar gas or DM annihilations is also shown.

Fig. 3: Schematic of ${}^{3}\overline{{{{\rm{He}}}}}$ production and propagation in our Galaxy.

Distribution of DM density ρ_DM in our Galaxy as a function of distance from the Galactic Centre according to the Navarro–Frenk–White profile⁶² (top). Graphical illustration of ${}^{3}\overline{{{{\rm{He}}}}}$ production from cosmic-ray interactions with interstellar gas or DM (χ) annihilations (bottom). The yellow halo represents the heliosphere and the Earth, Sun and positions of the Voyager 1, AMS-02 and GAPS experiments are depicted, too.

The propagation of charged particles within galaxies is driven by magnetic fields. The propagation is commonly described by a transport equation that includes the following terms: (1) a source function; (2) diffusion; (3) convection; (4) momentum variations due to Coulomb scattering, diffusion and ionization processes; (5) fragmentation, decays and inelastic interactions. This equation, discussed in more detail in Methods, can be numerically solved by employing several propagation models^63,64,65,66. In this work, the publicly available GALPROP code⁶⁶ is employed. In the context of this calculation, our Galaxy is approximated by a cylindrical disk filled with an interstellar gas composed of hydrogen (~90%) and ⁴He (~10%) with an average hydrogen number density of ~1 atom cm^–3 (ref. ⁶⁷). The gas distribution within our Galaxy is constrained by several astronomical spectroscopy measurements^68,69,70,71. GALPROP provides the propagation of particles up to the boundaries of the Solar System. To estimate the particle flux inside the Solar System, the effect of the solar magnetic field must be taken into account. This can be achieved by employing the force-field approximation or dedicated models like HelMod^72,73. The whole propagation chain is benchmarked using several species of cosmic rays, including protons and light nuclei (up to Z = 28)⁴⁶. The cosmic-ray injection spectra and the propagation parameters are tuned to match the measurements of protons and light nuclei both outside⁷⁴ and within^75,76,77 the Solar System.

After their production, the ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei need to travel a distance of several kiloparsecs to reach Earth^46,62. During this passage, they might encounter protons or ⁴He nuclei in interstellar gas and inelastically interact. Non-destructive inelastic processes can occur and cause a substantial energy loss that results in a so-called tertiary ${}^{3}\overline{{{{\rm{He}}}}}$ source peaked at low kinetic energies. Such a tertiary source component, however, only contributes a few percent of the total flux^30,31. We neglect this small contribution because we cannot distinguish between destructive and non-destructive inelastic processes. To model the total cross section of inelastic processes, we scale the momentum-dependent Geant4 parameterization of the ${}^{3}\overline{{{{\rm{He}}}}}$–p inelastic cross section with the correction factors obtained from our measurements. For the low-momentum range (1.17 ≤ p < 1.50 GeV c^–1), we consider the results from pp collisions and for the high-momentum range (1.50 ≤ p < 10.00 GeV c^–1), results from Pb–Pb collisions. The correction factors from the ALICE measurements and their uncertainties are parameterized with a continuous function employing a combination of polynomial and exponential functions. The additional uncertainty due to scaling with A is estimated to be lower than 8% (ref. ⁵⁴) (Methods). For the extrapolation to momenta above the measured momentum range, we consider the correction factor corresponding to the last measured momentum interval (Fig. 2, right). The resulting ${}^{3}\overline{{{{\rm{He}}}}}$–p inelastic cross section as a function of the ${}^{3}\overline{{{{\rm{He}}}}}$ kinetic energy per nucleon is shown in Extended Data Fig. 1 together with the Geant4 parameterization and the model employed in another work³⁰. The same procedure is applied to describe the ${}^{3}\overline{{{{\rm{He}}}}}$–⁴He inelastic processes. These scaled inelastic cross sections have been implemented in GALPROP.

The expected ${}^{3}\overline{{{{\rm{He}}}}}$ flux near Earth after all the propagation steps (Methods) with and without the effect of solar modulations is shown in the right and left panels of Fig. 4, respectively. Solar modulation is implemented using the force-field method⁷². The effect of inelastic interactions is demonstrated by showing the full propagation chain once with σ_inel(³$\overline{{{{\rm{He}}}}}$) set to zero and once with the inelastic cross section extracted from the ALICE measurement. Only the uncertainties relative to the measured σ_inel(³$\overline{{{{\rm{He}}}}}$) value are propagated and presented in Fig. 4. The inelastic collisions of ${}^{3}\overline{{{{\rm{He}}}}}$ with interstellar gas lead to a notable reduction in the expected flux for the signal candidates from DM as well as the background from cosmic-ray collisions.

Fig. 4: Expected ${}^{3}\overline{{{{\rm{He}}}}}$ flux near Earth before and after solar modulation.

Data before (left) and after (right) solar modulation. The latter is obtained using the force-field method with modulation potential ϕ = 400 MV. The results are shown as a function of kinetic energy per nucleon (E_kin/A). Fluxes for DM signal χ (red) and cosmic-ray background (blue) antihelium nuclei for different cases of inelastic cross sections used in the calculations (top). The bands show the results obtained with σ_inel(³$\overline{{{{\rm{He}}}}}$) from ALICE measurements, and the full lines correspond to the results using the parameterizations. The dashed lines show the fluxes obtained with σ_inel(³$\overline{{{{\rm{He}}}}}$) set to zero for the DM signal (orange line) and for the cosmic-ray background (magenta line). The green band on the x axis indicates the kinetic-energy range corresponding to the ALICE measurement for σ_inel(³$\overline{{{{\rm{He}}}}}$). Transparency of our Galaxy to the propagation of ${}^{3}\overline{{{{\rm{He}}}}}$ outside (left) and inside (right) the Solar System (bottom). The shaded areas (top right) show the expected sensitivity of the GAPS⁷⁹ and AMS-02³⁰ experiments. The top panels also show the fluxes obtained with σ_inel(³$\overline{{{{\rm{He}}}}}$) set to zero. Only the uncertainties relative to the measured σ_inel(³$\overline{{{{\rm{He}}}}}$) are shown, which represent standard deviations. The calculations employ the ${}^{3}\overline{{{{\rm{He}}}}}$ DM source described elsewhere²⁹ and the ${}^{3}\overline{{{{\rm{He}}}}}$ production cross section from the cosmic-ray background⁵⁷.

The transparency of our Galaxy to the ${}^{3}\overline{{{{\rm{He}}}}}$ passage is defined by the ratio of the flux obtained with and without the inelastic processes in GALPROP. The transparency values as a function of kinetic energy obtained with σ_inel(³$\overline{{{{\rm{He}}}}}$) from the Geant4 parameterization and from the ALICE measurements are shown in Fig. 4 (bottom) by the coloured lines and bands, respectively. The transparency profiles obtained with a solar modulation potential of 400 MV do not differ much from the non-modulated distributions (Fig. 4, bottom left and right). This is because the solar modulation reshuffles the yield from the more abundant high-momentum range to lower energies, but all the transparency profiles are rather flat as a function of particle energy. A transparency of the Galaxy of about 50% is estimated for ${}^{3}\overline{{{{\rm{He}}}}}$ from the considered DM source²⁹ and of about 25% for low-energy ${}^{3}\overline{{{{\rm{He}}}}}$ from cosmic-ray interactions⁵⁷. The latter increases further up to full transparency at higher energies. The different behaviour in the two cases is caused by both different underlying spectral shapes and different distributions of production points of the two sources, underlining the importance of full propagation studies (Methods). The employment of an alternative set of propagation parameters from ref. ⁷⁸ results in 40−60% lower transparency at low E_kin than using the propagation parameters from ref. ⁴⁶ (Methods).

The calculated ${}^{3}\overline{{{{\rm{He}}}}}$ transparency is found to be consistent—within uncertainties—with the Geant4 parameterization. It must be clearly noted that previously, it was not possible to quantify the uncertainty of the parameterizations employed in Geant4 or proposed elsewhere³⁰ due to the lack of experimental data. To quantify the improvement originating from our study, we, therefore, simply compare the full difference between no inelastic interaction and alternative parameterizations (~50% for the signal from DM and up to 75% for background) to our newly established uncertainties of about 10%–15% after solar modulation. We have, thus, verified that the uncertainty related to nuclear absorption is subleading with respect to other possible contributions in the cosmic-ray and DM modelling, particularly the production mechanism and propagation description^29,30,31,57. Note that the propagation example provided in this work does not cover the full range of uncertainties related to ${}^{3}\overline{{{{\rm{He}}}}}$ flux modelling (Methods); rather, it delivers a clear road map for future studies. The measured σ_inel(³$\overline{{{{\rm{He}}}}}$) and the developed methodology can be employed to carry out the propagation of ${}^{3}\overline{{{{\rm{He}}}}}$ using any DM or cosmic-ray interaction modelling as a source. Since a large separation between the signal and background is retained for low kinetic energies, our results clearly underline that the search for ${}^{3}\overline{{{{\rm{He}}}}}$ in space remains a very promising channel for the discovery of DM. These studies will be extended to ${}^{4}\overline{{{{\rm{He}}}}}$ and to the lower-momentum region in the near future with much larger datasets that will be collected in the coming few years.

Methods

Event selection

The inelastic pp and Pb–Pb events were recorded with the ALICE apparatus at collision energies of $\sqrt{s}$ = 13 TeV and $\sqrt{{s}_{{{{\rm{NN}}}}}}$ = 5.02 TeV, respectively. Events are triggered by the V0 detector comprising two plastic scintillator arrays placed on both sides of the interaction point and covering the pseudorapidity intervals of 2.8 < η < 5.1 and −3.7 < η < −1.7. The pseudorapidity is defined as $\eta =-\ln \left[\tan {\left( \frac{{{\Theta}}}{2}\right)}\right]$, where Θ is the polar angle of the particle with respect to the beam axis. The trigger condition is defined by the coincidence of signals in both arrays of the V0 detector. Together with the two innermost layers of the ITS detector, V0 is also used to reject background events like beam–gas interactions or collisions with mechanical structures of the beamline. For the analysis of pp data, a high-multiplicity trigger is employed to select only events with the total signal amplitude measured in the V0 detector above a certain threshold, which leads to a selection of about 0.17% of the inelastic pp collisions with the highest V0 signal. In these events, the number of charged particles produced at midrapidity ∣η∣ < 0.5 is about six times higher than 〈dN_ch/dy〉 = 5.31 ± 0.18 measured in inelastic pp collisions at $\sqrt{s}$ = 13 TeV (ref. ⁸⁰). This facilitates the analysis of rarely produced (anti)³He nuclei. As for the Pb–Pb experimental data, 10% of all inelastic events with the highest signal amplitude in the V0 detector are considered for the analysis. In these events, the average charged-particle multiplicity at midrapidity ∣η∣ < 0.5 amounts to 〈dN_ch/dy〉 = 1,764 ± 50 (ref. ⁸¹). In total, 147.9 × 10⁶ Pb–Pb and 10⁹ pp events were analysed.

Particle tracking and identification

Trajectories of charged particles are reconstructed in the ALICE central barrel from their hits in the ITS and TPC. The detectors are located inside a solenoidal magnetic field (0.5 T) bending the trajectories of charged particles. The curvature and direction of the charged-particle trajectories in the magnetic field are used to reconstruct their momentum. The detectors provide full azimuthal coverage in the pseudorapidity interval ∣η∣ < 0.9. This η range corresponds to the region within ±42° of the transverse plane that is perpendicular to the beam axis. Typical resolution of the transverse momentum reconstructed at the primary vertex (p_T,primary) for protons, pions and kaons varies from about 2% for tracks with p_T,primary = 10 GeV c^–1 to below 1% for p_T,primary ≤ 1 GeV c^–1.

Specific energy loss in the TPC gas is used to identify charged particles. Due to their electric charge (z = 2), high mass and quadratic dependence of specific energy loss on particle charge, ³He and ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei have larger energy loss than most other (anti)particles produced in collisions (like pions, kaons, protons and deuterons) and can be clearly identified in the TPC. The selected ³He candidates include a substantial amount of background from secondary nuclei that originate from spallation reactions in the detector material and can be seen at low momentum (Fig. 1b). This contribution is estimated via a fit to the distribution of the measured distance of closest approach between the track candidates and the primary collision vertex using templates from MC simulations. Since primary particles point back to the primary vertex, they are characterized by a distinct peak structure at zero distance of closest approach, whereas secondary particles correspond to a flat distribution of the distance of closest approach and their contribution can, therefore, be separated. More details on this procedure can be found elsewhere^12,47. For ³He candidates in pp collisions at $\sqrt{s}$ = 13 TeV, this contribution amounts to ~75% in the lowest analysed momentum interval of 0.65 ≤ p_primary/z < 0.80 GeV c^–1 and is negligible in the momentum range above p_primary/z = 1.50 GeV c^–1. For ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei, there is no contribution from spallation processes. In total, there are 16,801 ± 130 primary ${}^{3}\overline{{{{\rm{He}}}}}$ reconstructed in the TPC in the Pb–Pb data sample. In the sample of pp collisions, the total number of reconstructed primary candidates of ³He and ${}^{3}\overline{{{{\rm{He}}}}}$ is 773 ± 46 and 652 ± 30, respectively. The uncertainties for these values result from the fit to the TPC signal, which is used to reject the (small) background from (anti)triton nuclei misidentified as (anti)³He at low momenta.

Corrections and evaluation of systematic uncertainties

Due to continuous energy-loss effects in the detector material, the inelastic interaction of ${}^{3}\overline{{{{\rm{He}}}}}$ with the detector material happens at momentum p, which is lower than momentum p_primary reconstructed at the primary collision vertex. The corresponding effect is taken into account utilizing MC simulations in which one has precise information about both momenta for each (anti)particle. In the analysis of pp collisions, the average values of p/p_primary distributions in each analysed p_primary interval are used to consider the energy loss. The root mean square (r.m.s.) value of these distributions is used to determine the uncertainty in momentum p, which is propagated to the uncertainty of the measured cross section. For the analysis of the Pb–Pb data sample, the MC information on the momenta of daughter tracks originating from ${}^{3}\overline{{{{\rm{He}}}}}$ annihilation is used to estimate the corresponding effect and resulting uncertainty.

The systematic uncertainties due to tracking, particle identification and description of material budget in MC simulations are considered, and the total uncertainty is obtained as the quadratic sum of the individual contributions. The material budget of the ALICE apparatus^50,82,52 is varied by ±4.5% in MC simulations, and the deviations in the final results from the default case are considered as an uncertainty. The precision of ~4.5% of the MC parameterization is validated for the ALICE material with photon conversion analyses (up to the outer TPC vessel⁵⁰) and with tagged pion and proton absorption studies (for the material between TPC and TOF detectors⁵²).

For the Pb–Pb analysis, the total systematic uncertainty amounts to ~20% in the highest and lowest momentum intervals considered in the analysis and decreases to ≤10% in the momentum interval of 3 ≤ p < 7 GeV c^–1. For the analysis of pp data (which is based on the antibaryon-to-baryon ratio method), an additional uncertainty due to primordial antibaryon-to-baryon ratio produced in collisions is considered as a global uncertainty. The primordial antiproton-to-proton ratio of 0.998 ± 0.015 is extrapolated for the $\sqrt{s}$ = 13 TeV collision energy from available measurements^47,51; furthermore, under the assumption that the (anti)³He yield is proportional to the cube of the (anti)proton yield⁴², the primary ${}^{3}\overline{{{{\rm{He}}}}}{/}^{3}{{{\rm{He}}}}$ ratio amounts to 0.994 ± 0.045. This uncertainty is the dominant contribution to the total systematic uncertainty for the pp analysis, which amounts to ~8%.

MC simulation

The results presented in this Article are compared with the detailed MC simulations of the ALICE detector. The simulations start with the generation of (anti)particles at the primary collision vertex and the production of raw detector information, also taking into account inactive subdetector channels. The same reconstruction algorithms applied to real experimental data are employed to analyse the raw simulated data. For the pp analysis based on the antimatter-to-matter ratio, the primordial ${}^{3}\overline{{{{\rm{He}}}}}{/}^{3}{{{\rm{He}}}}$ ratio of 0.994 is used as an input for the MC simulations. Since the average multiplicity in pp collisions at midrapidity is low, no underlying event was simulated in this case. For the TOF-to-TPC analysis in Pb–Pb collisions, the simulations contain an underlying Pb–Pb event that was generated with the help of the HIJING event generator^83,84,85. On top of this underlying event, 160 nuclei of ${}^{3}\overline{{{{\rm{He}}}}}$ were injected following the momentum distribution obtained from independent studies on ${}^{3}\overline{{{{\rm{He}}}}}$ production¹².

For the propagation of (anti)particles through the detector material, the simulations rely on the Geant4 software package⁵³, in which the inelastic cross section of ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei is based on Glauber calculations. Since the Glauber model simulations are computationally too expensive to be performed during the propagation steps through the material, they are parameterized as a function of atomic mass number A of the target nucleus⁵⁴:

$${\sigma }_{hA}^{{{{\rm{inel}}}}}=\uppi \,{R}_{A}^{2}\ln \left(1+\frac{A{\sigma }_{hN}^{{{{\rm{tot}}}}}}{\uppi \,{R}_{A}^{2}}\right).$$

(1)

Here h denotes the nucleus in question (h = $\overline{{{{\rm{p}}}}}$, $\overline{{{{\rm{d}}}}}$, ${}^{3}\overline{{{{\rm{He}}}}}$ and ${}^{4}\overline{{{{\rm{He}}}}}$) and A is the atomic number of the target nucleus with radius R_A. Also, ${\sigma }_{hN}^{{{{\rm{tot}}}}}$ is the total (elastic plus inelastic) cross section of hadron h on nucleon N, which is estimated with the help of Glauber calculations by extrapolating the measured $\overline{{\rm{p}}}\rm{p}$ values⁵⁶ to larger antinuclei. We performed several full-scale MC simulations with varied inelastic cross sections of ${}^{3}\overline{{{{\rm{He}}}}}$ with matter, and the simulated observables used in this analysis are studied as a function of the inelastic cross-section re-scaling. This dependence is parameterized using the Lambert–Beer law (Fig. 1e,f). The parameterization reads as N_surv = N₀ × exp(–σ_inelρL), where N₀ corresponds to the number of incident particles, N_surv is the number of survived particles that did not get absorbed, σ_inel is the inelastic cross section, ρ is the density of the material crossed and L is the length of the particle trajectory in the material. The free parameter given by the product ρL is determined by a fit to the simulated observables.

To model the inelastic cross section of ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei in the interstellar medium, the Geant4 parameterization of the ${}^{3}\overline{{{{\rm{He}}}}}$–p inelastic cross section is scaled with the correction factors obtained from the ALICE measurements. The additional uncertainty that originates from re-scaling a measurement at 〈A〉 = 17.4 and 〈A〉 = 34.7 to A = 1 and A = 4 is taken from the difference between the parameterization for the dependence on A in Geant4 and in full Glauber calculation and amounts to <8% (ref. ⁵⁴). The resulting ${}^{3}\overline{{{{\rm{He}}}}}$–p inelastic cross section is shown in Extended Data Fig. 1 (left) together with the model employed in another work³⁰. The latter is based on the approximation that uses available measurements to estimate the inelastic antideuteron–proton cross section in the following way:

$${\sigma }_{{{{\rm{inel}}}}}^{\overline{{{{\rm{d}}}}}{{{\rm{p}}}}}\approx \frac{{\sigma }_{{{{\rm{tot}}}}}^{\overline{{{{\rm{d}}}}}{{{\rm{p}}}}}}{{\sigma }_{{{{\rm{tot}}}}}^{\overline{{{{\rm{p}}}}}{{{\rm{p}}}}}}({\sigma }_{{{{\rm{tot}}}}}^{\overline{{{{\rm{p}}}}}{{{\rm{p}}}}}-{\sigma }_{{{{\rm{el}}}}}^{\overline{{{{\rm{p}}}}}{{{\rm{p}}}}}).$$

(2)

By symmetry, the total antideuteron–proton cross section ${\sigma }_{{{{\rm{tot}}}}}^{\overline{{{{\rm{d}}}}}{{{\rm{p}}}}}$ is equal to the total deuteron–antiproton cross section taken from elsewhere⁸⁶. For antihelium, the inelastic cross section is scaled from antideuterons according to the mass number as ${\sigma }_{{{{\rm{inel}}}}}^{{}^{3}\overline{{{{\rm{He}}}}}{{{\rm{p}}}}}=\frac{3}{2}{\sigma }_{{{{\rm{inel}}}}}^{\overline{{{{\rm{d}}}}}{{{\rm{p}}}}}$. Extended Data Fig. 1 (right) also shows the resulting ${}^{3}\overline{{{{\rm{He}}}}}$–⁴He inelastic cross section obtained in the same way for the ⁴He target.

The results for the inelastic ${}^{3}\overline{{{{\rm{He}}}}}$ cross section are also tested against the modifications of elastic cross sections of ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei. Both ³He and ${}^{3}\overline{{{{\rm{He}}}}}$ elastic cross sections are independently varied by 30%, which led to ≤1% modifications of the final results. For the analysis of proton–proton collisions based on the antibaryon-to-baryon ratio method, the results are additionally investigated for the sensitivity to the ³He inelastic cross section. The latter is varied by 10%, which is the uncertainty of the Geant4 parameterizations obtained from fits to the experimental data⁸⁷. This variation yields a modification of ≤2.3% in the reconstructed antihelium-to-helium ratio.

Propagation modelling

The possible sources of antinuclei in our Galaxy are either cosmic-ray interactions with nuclei in the interstellar gas or more exotic sources such as DM annihilations or decays. Cosmic rays mainly consist of protons and originate from supernovae remnants, whereas DM has so far escaped direct or indirect detection but its density profile can be modelled⁸⁸.

The propagation in the Galaxy can be carried out using the publicly available propagation models^63,64,65,66. We choose the GALPROP code (version 56 available at https://galprop.stanford.edu) for the implementation of ${}^{3}\overline{{{{\rm{He}}}}}$ cosmic-ray propagation, which is discussed in detail elsewhere⁸⁹. GALPROP numerically solves a general transport equation for all the included particle species⁶⁶. This transport equation reads as

$$\begin{array}{l}\frac{\partial \psi }{\partial t}=q({{{\bf{r}}}},p)+\nabla \cdot ({D}_{xx}{{{\bf{grad}}}}\psi -{{{\bf{V}}}}\psi )\\+\frac{\partial }{\partial p}{p}^{2}{D}_{\mathrm{pp}}\frac{\partial }{\partial p}\frac{\psi }{{p}^{2}}-\frac{\partial }{\partial p}\left[\psi \frac{{{{\rm{d}}}}p}{{{{\rm{d}}}}t}-\frac{p}{3}(\nabla \cdot {{{\bf{V}}}})\psi \right]-\frac{\psi }{\tau }.\end{array}$$

(3)

Here ψ = ψ(r, p, t) is the time-dependent ${}^{3}\overline{{{{\rm{He}}}}}$ density per unit of the total particle momentum and q(r, p) is the source function for ${}^{3}\overline{{{{\rm{He}}}}}$. The second and third terms describe the propagation of ${}^{3}\overline{{{{\rm{He}}}}}$, where D_xx, V and D_pp are the spatial diffusion coefficient, convection velocity and diffusive re-acceleration coefficient, respectively. Although the effect of the Galactic magnetic field is not explicitly modelled, it is accounted for by these terms of the transport equation. These coefficients are the same for all the particle species and can be constrained using available cosmic-ray measurements. We use the best-fit values of these parameters provided elsewhere⁴⁶. The fourth term accounts for momentum losses via cosmic-ray interactions with interstellar gas (dp/dt) and adiabatic momentum losses (∇ ⋅ V). The last term represents the ${}^{3}\overline{{{{\rm{He}}}}}$ inelastic collisions with interstellar gas, where 1/τ is the fragmentation rate. It is related to the inelastic cross section as follows:

$$\frac{1}{\tau }=\beta c\left({n}_{\mathrm{H}}({{{\bf{r}}}}){\sigma }_{{{{\rm{inel}}}}}^{{}^{3}\overline{{{{\rm{He}}}}}{{{\rm{p}}}}}(p)+{n}_{\mathrm{He}}({{{\bf{r}}}}){\sigma }_{{{{\rm{inel}}}}}^{{}^{3}{\overline{{{{\rm{He}}}}}}{{{^{4}\rm{He}}}}}(p)\right).$$

(4)

The elastic re-scattering of cosmic-ray antinuclei in the interstellar medium is assumed to have a negligible effect on diffusive propagation⁹⁰. The second and third terms in equation (3) can cause both acceleration and deceleration, which means that the final flux at a given energy also depends on the initial fluxes at both higher and lower energies. Therefore, the final number of particles in a specific energy interval depends on (i) the energy spectrum and spatial distribution of the source, (2) propagation parameters, (3) particles’ momentum loss/gain and (4) annihilation cross section. Only the first and last terms of equation (3) require particle-specific information. Here ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei can be produced when cosmic-ray particles interact with protons or ⁴He nuclei in the interstellar medium. The ${}^{3}\overline{{{{\rm{He}}}}}$ source function in this case is

$$q({{{\bf{r}}}},p)=\mathop{\sum}\limits_{{{{\rm{CR}}}}={{{\rm{H}}}},{{{\rm{He}}}}}\,\mathop{\sum}\limits_{{{{\rm{ISM}}}}={{{\rm{H}}}},{{{\rm{He}}}}}{n}_{{{{\rm{ISM}}}}}({{{\bf{r}}}})\int {{{\rm{d}}}}{p}_{{{{\rm{CR}}}}}^{\prime}\,{\beta }_{{{{\rm{CR}}}}}\,c\frac{{{{\rm{d}}}}\sigma \left(p,{p}_{{{{\rm{CR}}}}}^{\prime}\right)}{{{{\rm{d}}}}p}\,{n}_{{{{\rm{CR}}}}}\left({{{\bf{r}}}},{p}_{{{{\rm{CR}}}}}^{\prime}\right).$$

(5)

The density of hydrogen and helium gas is represented by n_ISM(r), and ${p}_{{{{\rm{CR}}}}}^{\prime}$, β_CR and ${n}_{{{{\rm{CR}}}}}({{{\bf{r}}}},{p}_{{{{\rm{CR}}}}}^{\prime})$ are the momentum, velocity and density of cosmic rays, respectively, whereas p is the momentum of the produced ${}^{3}\overline{{{{\rm{He}}}}}$. Also, ${{{\rm{d}}}}\sigma (p,{p}_{{{{\rm{CR}}}}}^{\prime})/{{{\rm{d}}}}p$ is the ${}^{3}\overline{{{{\rm{He}}}}}$ differential production cross section for the specific collision and includes primary ${}^{3}\overline{{{{\rm{He}}}}}$ as well as the products of $\overline{t}$ decays. The most abundant cosmic rays are protons and helium; thus, this source function must be calculated for both species and summed up. In another work⁵⁷, all the relevant types of collision between protons and ⁴He nuclei with projectile beam energies ranging from 31.0 GeV to 12.5 TeV are considered, and the so-called spherical approximation is used in which antinucleons with a momentum difference smaller than p₀ are forming an antinucleus^57,91. The parameter p₀ depends on the collision energy and is constrained by several accelerator-based measurements^{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17}, including measurements at the LHC^92,93. The resulting injection spectra obtained from the collisions of cosmic rays with the interstellar medium peak above 7 GeV A^–1 (ref. ⁵⁷).

In the case of ${}^{3}\overline{{{{\rm{He}}}}}$ nuclei produced from DM annihilations, the source function depends on the thermally averaged annihilation cross section times the velocity (〈σv〉), density (ρ_DM) of the DM, mass (m_χ) of the DM particle and the resulting ${}^{3}\overline{{{{\rm{He}}}}}$ spectrum (dN/dE_kin) (ref. ²⁹):

$$q({{{\bf{r}}}},{E}_{{{{\rm{kin}}}}})=\frac{1}{2}\frac{{\rho }_{{{{\rm{DM}}}}}^{2}({{{\bf{r}}}})}{{m}_{\chi }^{2}}\langle \sigma v\rangle \frac{{{{\rm{d}}}}N}{{{{\rm{d}}}}{E}_{{{{\rm{kin}}}}}}.$$

(6)

Here E_kin is the kinetic energy of the produced ${}^{3}\overline{{{{\rm{He}}}}}$ including those that are the products of $\overline{t}$ decays. The spectrum is calculated utilizing the PYTHIA 8.156 event generator⁹⁴ and a coalescence model with a coalescence momentum p₀ = 357 MeV c^–1, as described in more detail elsewhere²⁹. We set 〈σv〉 = 2.6 × 10⁻²⁶ cm³ s⁻¹ (ref. ³⁰). We implemented the Navarro–Frenk–White profile in GALPROP, which is one of the most commonly used DM density profiles:

$$\rho (r)=\frac{{\rho }_{0}}{\frac{r}{{R}_{\mathrm{s}}}{\left(1+\frac{r}{{R}_{\mathrm{s}}}\right)}^{2}}.$$

(7)

Here r is the distance to the Galactic Centre, ρ₀ is an overall normalization such that ρ(r) is equal to the local density ρ_⊙ = 0.39 GeV cm^–3 at r = 8.5 kpc and R_s = 24.42 kpc is a scale radius²⁹. In contrast to the spectra of ${}^{3}\overline{{{{\rm{He}}}}}$ from collisions of cosmic rays with the interstellar medium, the resulting spectrum for ${}^{3}\overline{{{{\rm{He}}}}}$ originating from DM annihilation peaks at low kinetic energies of around 0.1 GeV A^–1 (ref. ²⁹).

Discussion of uncertainties on ${}^{3}\overline{{{{\rm{He}}}}}$ cosmic-ray modelling

The results presented in this paper focus on the impact of ALICE measurements for σ_inel(³$\overline{{{{\rm{He}}}}}$) on the cosmic-ray ${}^{3}\overline{{{{\rm{He}}}}}$ flux and the corresponding transparency of the Galaxy. To this purpose, we have considered two models of ${}^{3}\overline{{{{\rm{He}}}}}$ sources described in the main text and only propagated the uncertainty of the σ_inel(³$\overline{{{{\rm{He}}}}}$) measurement. Here we briefly discuss other possible uncertainties related to the ${}^{3}\overline{{{{\rm{He}}}}}$ cosmic-ray modelling.

As for the DM source, it is apparent that a different DM mass assumption changes the antinuclei flux profile near Earth^22,29,31. The DM mass assumptions around m_χ ≈ 100 GeV are favoured by recent AMS-02 antiproton data³¹; for very different values of m_χ, the ${}^{3}\overline{{{{\rm{He}}}}}$ flux and the corresponding transparency can be studied as described in this work. Variation in the DM annihilation cross section 〈σv〉 leads to a constant scaling of ${}^{3}\overline{{{{\rm{He}}}}}$ flux according to equation (6) and therefore to identical transparency values. Although the Navarro–Frenk–White profile is used in this work to describe the distribution of DM in the Galaxy, other profiles are also available such as Einasto²², Burkert⁹⁵ or the isothermal one⁹⁶. Antiproton limits on 〈σv〉 are partially degenerate with the effect of different DM profiles, and the overall impact of varying the DM profiles on the maximum allowed antinuclei flux is minor ^30,61. If the isothermal profile is employed instead of the Navarro–Frenk–White one, the obtained ${}^{3}\overline{{{{\rm{He}}}}}$ transparency is shifted up by 10%−15%.

Although coalescence-based models can successfully describe antinuclei production, the model uncertainties are still relatively large, which leads to substantial changes in the magnitude of antinuclei fluxes^22,30,61. In general, as long as different coalescence models retain the shape of the produced antinuclei momentum spectrum, the resulting transparency is not affected. For example, the change in coalescence parameter p₀ leads to constant scaling of the antinuclei flux and identical transparency values.

The GALPROP parameters used in this work are tuned to reproduce the available experimental data on cosmic-ray nuclei (up to Z = 28). The obtained uncertainties on the nuclei fluxes of ≲10% (ref. ⁴⁶) are not considered in this work, since they result in a negligible change in ${}^{3}\overline{{{{\rm{He}}}}}$ fluxes. An alternative set of propagation parameters has been obtained⁷⁸ by considering a subsample of the available cosmic-ray data. The comparison between the two sets is discussed in more details elsewhere⁶¹. The employment of these alternative parameters decreases the ${}^{3}\overline{{{{\rm{He}}}}}$ background flux by one order of magnitude at the lowest E_kin value considered in this work and results in about 60% lower transparency. For the DM signal, the corresponding flux is up to a factor of five higher at the lowest E_kin value with about 40% lower transparency. These differences in fluxes and transparencies are obtained before the solar modulation and become minor for E_kin ≳ 10 GeV A^–1, for the DM signal as well as the background.