Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Entanglement spread area law in gapped ground states

Nature Physics volume 18, pages 1362–1366 (2022)Cite this article

Subjects

Abstract

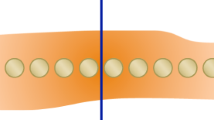
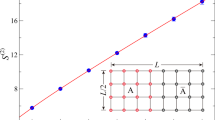
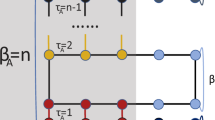
Ground-state entanglement governs various properties of quantum many-body systems at low temperatures and is the key to understanding gapped quantum phases of matter. Here we identify a structural property of entanglement in the ground state of gapped local Hamiltonians. This property is captured using a quantum information quantity known as the entanglement spread, which measures the difference between Rényi entanglement entropies. Our main result shows that gapped ground states possess limited entanglement spread across any partition of the system, exhibiting an area-law scaling. Our result applies to systems with interactions described by any graph, but we obtain an improved bound for the special case of lattices. These interaction graphs include cases where entanglement entropy is known not to satisfy an area law. We achieve our results first by connecting the ground-state entanglement to the communication complexity of testing bipartite entangled states and then devising a communication scheme for testing ground states using recently developed quantum algorithms for Hamiltonian simulation.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Entanglement spectrum across a general partition.
Fig. 2: Smooth entanglement spread.
Fig. 3: Communication complexity of identity testing.

Similar content being viewed by others

Data availability

No data or code have been generated in this work.

References

  1. Briegel, H. J., Browne, D. E., Dür, W., Raussendorf, R. & Van den Nest, M. Measurement-based quantum computation. Nat. Phys. 5, 19–26 (2009).

    Article  Google Scholar 

  2. Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395 (1983).

    Article  ADS  Google Scholar 

  3. Bardeen, J., Cooper, L. N. & Schrieffer, J. R. Theory of superconductivity. Phys. Rev. 108, 1175 (1957).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Broholm, C. et al. Quantum spin liquids. Science 367, eaay0668 (2020).

    Article  Google Scholar 

  5. Sachdev, S. Quantum phase transitions. in Handbook of Magnetism and Advanced Magnetic Materials (2006).

  6. Hastings, M. B. An area law for one-dimensional quantum systems. J. Stat. Mech. 2007, P08024 (2007).

    Article  MathSciNet  MATH  Google Scholar 

  7. Arad, I., Kitaev, A., Landau, Z. & Vazirani, U. An area law and sub-exponential algorithm for 1D systems. Preprint at https://arxiv.org/abs/1301.1162 (2013).

  8. Brandão, Fernando, G. S. L. & Horodecki, M. An area law for entanglement from exponential decay of correlations. Nat. Phys. 9, 721–726 (2013).

    Article  Google Scholar 

  9. White, S. R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 69, 2863–2866 (1992).

    Article  ADS  Google Scholar 

  10. Landau, Z., Vazirani, U. & Vidick, T. A polynomial time algorithm for the ground state of one-dimensional gapped local Hamiltonians. Nat. Phys. 11, 566–569 (2015).

    Article  Google Scholar 

  11. Masanes, L. Area law for the entropy of low-energy states. Phys. Rev. A 80, 052104 (2009).

    Article  ADS  Google Scholar 

  12. de Beaudrap, N., Osborne, T. J. & Eisert, J. Ground states of unfrustrated spin Hamiltonians satisfy an area law. New J. Phys. 12, 095007 (2010).

    Article  MATH  Google Scholar 

  13. Cho, J. Sufficient condition for entanglement area laws in thermodynamically gapped spin systems. Phys. Rev. Lett. 113, 197204 (2014).

    Article  ADS  Google Scholar 

  14. Brandão, F. G. S. L. & Cramer, M. Entanglement area law from specific heat capacity. Phys. Rev. B 92, 115134 (2015).

    Article  ADS  Google Scholar 

  15. Anshu, A., Arad, I. & Gosset, D. Entanglement subvolume law for 2D frustration-free spin systems. In Proc. 52nd Annual ACM SIGACT Symposium on Theory of Computing (STOC 2020) 868–874 (ACM, 2020).

  16. Anshu, A., Arad, I. & Gosset, D. An area law for 2D frustration-free spin systems. Preprint at https://arxiv.org/abs/2103.02492 (2021).

  17. Aharonov, D. et al. Local tests of global entanglement and a counterexample to the generalized area law. In Proc. 2014 IEEE 55th Annual Symposium on Foundations of Computer Science FOCS14 246–255 (IEEE, 2014).

  18. Sachdev, S. & Ye, J. Gapless spin-fluid ground state in a random quantum Heisenberg magnet. Phys. Rev. Lett. 70, 3339–3342 (1993).

    Article  ADS  Google Scholar 

  19. Song, C. et al. Generation of multicomponent atomic Schrödinger cat states of up to 20 qubits. Science 365, 574–577 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  20. Omran, A. et al. Generation and manipulation of Schrödinger cat states in Rydberg atom arrays. Science 365, 570–574 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  21. Bluvstein, D. et al. A quantum processor based on coherent transport of entangled atom arrays. Nature 604, 451–456 (2022).

  22. Li, H. & Haldane, F. D. M. Entanglement spectrum as a generalization of entanglement entropy: identification of topological order in non-Abelian fractional quantum Hall effect states. Phys. Rev. Lett. 101, 010504 (2008).

    Article  ADS  Google Scholar 

  23. Pollmann, F., Turner, A. M., Berg, E. & Oshikawa, M. Entanglement spectrum of a topological phase in one dimension. Phys. Rev. B 81, 064439 (2010).

    Article  ADS  Google Scholar 

  24. Schuch, N., Poilblanc, D., Cirac, J. I. & Pérez-García, D. Topological order in the projected entangled-pair states formalism: transfer operator and boundary Hamiltonians. Phys. Rev. Lett. 111, 090501 (2013).

    Article  ADS  Google Scholar 

  25. Cirac, J. I., Poilblanc, D., Schuch, N. & Verstraete, F. Entanglement spectrum and boundary theories with projected entangled-pair states. Phys. Rev. B 83, 245134 (2011).

    Article  ADS  Google Scholar 

  26. Kato, K. & Brandão, F. G. S. L. Locality of edge states and entanglement spectrum from strong subadditivity. Phys. Rev. B 99, 195124 (2019).

    Article  ADS  Google Scholar 

  27. Dalmonte, M., Vermersch, B. & Zoller, P. Quantum simulation and spectroscopy of entanglement Hamiltonians. Nat. Phys. 14, 827–831 (2018).

    Article  Google Scholar 

  28. Anshu, A., Arad, I. & Jain, A. How local is the information in tensor networks of matrix product states or projected entangled pairs states. Phys. Rev. B 94, 195143 (2016).

    Article  ADS  Google Scholar 

  29. Verstraete, F., Murg, V. & Cirac, J. I. Matrix product states, projected entangled pair states, and variational renormalization group methods for quantum spin systems. Adv. Phys. 57, 143–224 (2008).

    Article  ADS  Google Scholar 

  30. Hayden, P. & Winter, A. Communication cost of entanglement transformations. Phys. Rev. A 67, 012326 (2003).

    Article  ADS  Google Scholar 

  31. König, R., Renner, R. & Schaffner, C. The operational meaning of min- and max-entropy. IEEE Trans. Inf. Theory 55, 4337–4347 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  32. Berta, M. Single-Shot Quantum State Merging. Master’s thesis, ETH Zurich (2009).

  33. Tomamichel, M. A Framework for Non-Asymptotic Quantum Information Theory. PhD thesis, ETH Zurich (2012).

  34. Hastings, M. B. Lieb-Schultz-Mattis in higher dimensions. Phys. Rev. B 69, 104431 (2004).

  35. Hastings, M. B. & Koma, T. Spectral gap and exponential decay of correlations. Commun. Math. Phys. 265, 781–804 (2006).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  36. Nachtergaele, B. & Sims, R. Lieb-Robinson bounds and the exponential clustering theorem. Commun. Math. Phys. 265, 119–130 (2006).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  37. Lo, H.-K. & Popescu, S. Classical communication cost of entanglement manipulation: is entanglement an interconvertible resource? Phys. Rev. Lett. 83, 1459 (1999).

    Article  ADS  Google Scholar 

  38. Coudron, M. & Harrow, A. W. Universality of EPR pairs in entanglement-assisted communication complexity, and the communication cost of state conversion. In 34th Computational Complexity Conference, LIPIcs, Leibniz International Proceedings in Informatics 20 (Schloss Dagstuhl, Leibniz Center for Informatics, 2019).

  39. Harrow, A. W. & Leung, D. W. A communication-efficient nonlocal measurement with application to communication complexity and bipartite gate capacities. IEEE Trans. Inf. Theory 57, 5504–5508 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  40. Aharonov, D., Arad, I., Landau, Z. & Vazirani, U. The detectability lemma and quantum gap amplification. In Proc. Forty-First Annual ACM Symposium on Theory of Computing STOC’09 417–426 (ACM, 2009).

  41. Arad, I., Landau, Z. & Vazirani, U. Improved one-dimensional area law for frustration-free systems. Phys. Rev. B 85, 195145 (2012).

    Article  ADS  Google Scholar 

  42. Bravyi, S., DiVincenzo, D. P., Oliveira, R. & Terhal, B. M. The complexity of stoquastic local Hamiltonian problems. Quantum Inf. Comput. 8, 361–385 (2008).

    MathSciNet  MATH  Google Scholar 

  43. Chandran, A., Khemani, V. & Sondhi, S. L. How universal is the entanglement spectrum? Phys. Rev. Lett. 113, 060501 (2014).

    Article  ADS  Google Scholar 

  44. Araki, H. Gibbs states of a one dimensional quantum lattice. Commun. Math. Phys. 14, 120–157 (1969).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  45. Pérez-García, D. & Pérez-Hernández, A. Locality estimes for complex time evolution in 1D. Preprint at https://arxiv.org/abs/2004.10516 (2020).

  46. Schuch, N., Wolf, M. M., Verstraete, F. & Cirac, J. I. Computational complexity of projected entangled pair states. Phys. Rev. Lett. 98, 140506 (2007).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  47. Kim, I. H. Entropy scaling law and the quantum marginal problem. Phys. Rev. X 11, 021039 (2021).

    Google Scholar 

  48. Arad, I., Landau, Z., Vazirani, U. & Vidick, T. Rigorous RG algorithms and area laws for low energy eigenstates in 1D. Commun. Math. Phys. 356, 65–105 (2017).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  49. Childs, A. M., Su, Y., Tran, M. C., Wiebe, N. & Zhu, S. A theory of trotter error. Preprint at https://arxiv.org/abs/1912.08854 (2019).

  50. Guang H. L. & Wiebe, N. Hamiltonian simulation in the interaction picture. Preprint at https://arxiv.org/abs/1805.00675 (2018).

  51. Berry, D. W., Childs, A. M., Cleve, R., Kothari, R. & Somma, R. D. Simulating Hamiltonian dynamics with a truncated taylor series. Phys. Rev. Lett. 114, 090502 (2015).

    Article  ADS  Google Scholar 

  52. Touchette, D. Quantum information complexity. In Proc. Forty-Seventh Annual ACM on Symposium on Theory of Computing STOC ’15 317–326 (ACM, 2015).

  53. Kuwahara, T. & Saito, K. Area law of noncritical ground states in 1D long-range interacting systems. Nat. Commun. 11, 4478 (2020).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

A.W.H. thanks D. Aharonov for insightful discussions regarding this project and raising the question of connection between the communication complexity of measuring the ground state and ground-state entanglement. A.A. thanks D. Gosset for discussions on the applications of quantum algorithms to area laws. M.S. thanks Z. Landau, A. Natarajan and U. Vazirani for helpful discussions. We thank I. Arad for suggesting the connection between entanglement spread and tensor network contraction. A.A. acknowledges support through the NSF award QCIS-FF: Quantum Computing & Information Science Faculty Fellow at Harvard University (NSF 2013303). Part of the work was done when A.A. was affiliated to the Institute for Quantum Computing and the Department of Combinatorics and Optimization, University of Waterloo, and the Perimeter Institute for Theoretical Physics, where research was supported by the Canadian Institute for Advanced Research, through funding provided to the Institute for Quantum Computing by the Government of Canada and the Province of Ontario. Perimeter Institute is also supported in part by the Government of Canada and the Province of Ontario. A.W.H. was funded by NSF grants CCF-1452616, CCF-1729369 and PHY-1818914; the NSF QLCI program through grant number OMA-2016245; and a Samsung Advanced Institute of Technology Global Research Partnership. M.S. was funded by NSF grant CCF-1729369.

Author information

Authors and Affiliations

  1. School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, USA

    Anurag Anshu

  2. Center for Theoretical Physics, Massachusetts Institute of Technology, Cambridge, MA, USA

    Aram W. Harrow & Mehdi Soleimanifar

Authors
  1. Anurag Anshu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Aram W. Harrow
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mehdi Soleimanifar
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All the authors contributed equally to all aspects of this work. The authors are arranged alphabetically by last name.

Corresponding author

Correspondence to Aram W. Harrow.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Renato Renner and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Sections 1–3.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Anshu, A., Harrow, A.W. & Soleimanifar, M. Entanglement spread area law in gapped ground states. Nat. Phys. 18, 1362–1366 (2022). https://doi.org/10.1038/s41567-022-01740-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01740-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing