Flavour-selective localization in interacting lattice fermions

Abstract

A large repulsion between particles in a quantum system can lead to their localization, an effect responsible for the Mott insulator phases in strongly correlated materials. In a system with multiple orbitals, an orbital-selective Mott insulator can form, where electrons in some orbitals are predicted to localize while others remain itinerant. Here we demonstrate a more general version of this phenomenon by observing flavour-selective localization in an atom-based quantum simulator. Our experiment realizes Fermi–Hubbard models with an SU(3) symmetry that can be broken using a tunable coupling between flavours. We observe an enhancement of the localization associated with a selective Mott transition and the emergence of flavour-dependent correlations. Our realization of flavour-selective Mott physics demonstrates the potential of cold atoms to simulate interacting multicomponent materials such as superconductors and topological insulators.

Main

Interactions shape the collective behaviour of many-particle quantum systems, leading to rich phase diagrams where conventional and novel phases can be induced by a controlled variation of external stimuli. The most direct example is perhaps the Mott insulator, where the large repulsion among particles leads to an insulating state despite the non-interacting system being a metal or a superfluid¹. In solid-state physics, the interest in Mott insulators is reinforced by the observation that the proximity to a Mott transition is a horn of plenty where a variety of spectacular phases can be observed, high-temperature superconductivity^2,3 being only the tip of the iceberg⁴.

In recent years, it has become clear that the standard SU(2) Fermi–Hubbard model is only one specific example, as many interesting materials require a description in terms of ‘multicomponent’ Hubbard models, for example when the conduction electrons have an additional orbital degree of freedom. These systems are not merely more complicated but rather host new phenomena, challenging the standard paradigm of Mott localization⁵. Indeed, when the symmetry between orbitals is broken, by some field or internal coupling, electrons in specific orbitals (or some combinations of them) can be Mott-localized while others remain itinerant, leading to surprising ‘orbital-selective Mott insulators’⁶.

Orbital-selective Mott physics has become a central concept for the description of a new class of high-T_c superconductors based on iron⁷, as it can describe the anomalies of the metallic state^8,9,10 and the orbital character of superconductivity¹¹ in those systems. However, a clean observation of selective Mott transitions is intrinsically hard in solid-state systems because of the limited experimental control over the microscopic parameters and the orbital degree of freedom. The paradigm of selective Mott physics is itself far from being fully explored and has the potential to become a powerful framework to understand a variety of phenomena, from superconductivity to topological properties, in multicomponent quantum materials.

In this work, we take a broader perspective and treat orbital-selective Mott physics as an example of the general concept of flavour-selective Mott localization¹², which can be realized in a variety of multi-flavour systems, where the flavour can be the spin, the orbital or any other quantum number. We realize a minimal instance of this phenomenon by means of an atomic quantum simulator based on the optical manipulation of nuclear-spin mixtures of ultracold two-electron ¹⁷³Yb atoms. This platform allows the realization of multicomponent systems with global SU(N) interaction symmetry (where N is the number of components)^13,14, as in recent works reporting the realization of SU(N) quantum wires¹⁵, SU(N) Mott insulators^16,17 and, more recently, SU(N) quantum magnetism¹⁸. Here, we introduce an approach to break the symmetry of SU(3) Fermi–Hubbard systems in a controlled way, which allows us to go beyond the investigations in the solid state and to observe directly the two key signatures of selective Mott physics¹²: an overall enhancement of Mott localization and the onset of flavour-selective correlations.

The experiment is performed with three-component ultracold ¹⁷³Yb Fermi gases with total atom number up to N = 4 × 10⁴ and initial temperature T ≃ 0.2T_F (where T_F is the Fermi temperature for the single-component gas). The atoms are then trapped in a cubic three-dimensional (3D) optical lattice (lattice constant d = λ/2 = 380 nm), which realizes the multi-flavour Hubbard Hamiltonian

$$\begin{array}{ll}\hat{H}=&-t\mathop{\sum}\limits_{\langle i,j\rangle ,\alpha }\left({\hat{c}}_{\alpha i}^{{\dagger} }{\hat{c}}_{\alpha j}+{{{\rm{h.c.}}}}\right)+U\mathop{\sum}\limits_{i,\alpha ,\beta \ne \alpha }{\hat{n}}_{\alpha i}{\hat{n}}_{\beta i}+{\hat{V}}_{\mathrm{T}}\\ &+\frac{{{\varOmega }}}{2}\mathop{\sum}\limits_{i}\left({\hat{c}}_{1i}^{{\dagger} }{\hat{c}}_{2i}+{{{\rm{h.c.}}}}\right)\end{array}$$

(1)

where α, β ∈ {1, 2, 3} indicate the fermionic flavours (corresponding to nuclear spin states m = +5/2, +1/2 and −5/2, respectively), ${{\hat{c}}^{\dagger}_{\alpha i}}$ is the destruction operator for a fermion of flavour α in site i (h. c. denotes the Hermitian conjugate operator), ${{{\hat{n}}_{\alpha i}={\hat{c}}^{\dagger}_{\alpha i}} {\hat{c}}_{\alpha i}}$ is the corresponding number operator, t is the tunnelling energy between nearest-neighbouring sites 〈i, j〉, U is the on-site repulsion energy between two atoms of different flavours and ${\hat{V}}_{\mathrm{T}}=\kappa {\sum }_{i,\alpha }{R}_{i}^{2}{\hat{n}}_{\alpha i}$ describes the effects of a slowly varying harmonic trapping potential (where R_i is the distance of site i from the trap centre and κ describes the strength of the trap). This last term determines the density in the lattice. In the non-interacting case (U = 0) the average filling at T = 0 and Ω = 0 can be calculated as ~1.8 atoms per site for the mean atom number of N = 2 × 10⁴ considered in the experiments discussed below, while in the strongly interacting limit (t = 0 and Ω = 0) it reduces to 1 atom per site (corresponding to the formation of Mott domains) (Supplementary Information). In the absence of the fourth term of equation (1), $\hat{H}$ has an intrinsic global SU(3) symmetry, which is ensured by the lack of variation of the atom–atom interactions with the spin state and by the realization of spin-independent optical potentials, that is, that U, t and κ do not depend on α. This symmetry is explicitly broken by the fourth term, which describes a coherent on-site coupling between flavours $\left|1\right\rangle$ and $\left|2\right\rangle$. This coupling is provided by a two-photon Raman process with a Rabi frequency of Ω/h (Supplementary Information) (where h is the Planck constant). At the single-particle level, this coupling lifts the degeneracy between the flavours, creating two dressed combinations $\left|\pm \right\rangle =\left(\left|1\right\rangle \pm \left|2\right\rangle \right)/\sqrt{2}$, energy-shifted from $\left|3\right\rangle$ by ±Ω/2, as sketched in Fig. 1c.

Fig. 1: Sketch of the physical system.

a, We consider a system of repulsively SU(3)-interacting fermions in a lattice. The global symmetry is broken by a coherent Rabi driving Ω between two internal states. b, In the absence of coupling, the system experiences a phase transition from an SU(3) metal to a Mott insulator as the hopping is reduced. c, The Rabi driving lifts the degeneracy between the states and, in a dressed basis picture, causes them to acquire different energies. The competition with the hopping can drive a transition from a metal to an insulator already in the non-interacting case. The energy band diagrams refer to the simplified case of a homogeneous system at a constant Fermi energy.

We use an adiabatic preparation sequence to produce an equilibrium state of the atomic mixture in the optical lattice, with equal state populations N₁ = N₂ = N₃ = N/3 and in the presence of the coherent coupling Ω between states $\left|1\right\rangle$ and $\left|2\right\rangle$ (Supplementary Information). To characterize the degree of localization of the particles in the lattice, we measure the number of atoms N_d in doubly occupied sites (called ‘doublons’ in the following) with photoassociation spectroscopy, as in previous experiments that demonstrated the onset of Mott localization for ultracold fermions (refs. ^16,19 and Supplementary Information). Figure 2a reports typical measurements of N_d as a function of the total atom number N. In a harmonically trapped system, the rate of change of N_d with respect to N provides information on the core compressibility^19,20. A vanishing value of N_d over an extended range of N signals the presence of an incompressible state with one atom per site in the centre of the trap (since adding particles does not lead to a proportional increase of doublons), while the critical N above which N_d then departs from zero can be connected to the magnitude of the energy gap protecting the localized phase. Figure 2a shows two datasets for U = 2.6D (where D = 6t is the tunnelling energy times the lattice coordination number) and two different Rabi couplings Ω = 0 and Ω = 1.6D, respectively. A comparison between the two datasets clearly shows that the Rabi coupling Ω results in an enhanced suppression of doublons, enlarging the region of N where the incompressible state forms.

Fig. 2: Measurement of double occupancies.

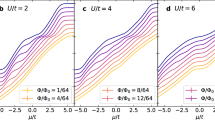
a, Number of atoms in doubly occupied sites N_d as a function of the total atom number N for two different values of Ω and the same U = 2.6D. b, Average doublon fraction f_d as a function of U/D and Ω/D. The actual measurements are marked by the points. c,d, Subsets of the data for two different cross sections of the plot in b, that is, for Ω = 0 (c) and for U = 2.6D (d). The measurements in b–d are averages over an interval N = (5–35) × 10³. Error bars in a, c and d are obtained by a bootstrap analysis (Supplementary Information). Dashed lines in a are fits with a piecewise function (null + straight line), while colour shades in c and d are guides to the eye representing the experimental uncertainty.

Source data

In the following, we take the doublon fraction f_d = 〈N_d/N〉, averaged over the N interval marked by the grey region in Fig. 2a as an indicator of the degree of Mott localization of the system. The measured values of f_d are shown as a function of U and Ω in Fig. 2b, clearly revealing the cooperative effect of Rabi coupling and repulsive interactions driving the system towards a Mott localized state. The same data are plotted with error bars in Fig. 2c,d along two different line cuts of the diagram in Fig. 2b. Figure 2c shows the effect of an increasing U in the transition towards an SU(3) Mott insulator for Ω = 0, while Fig. 2d shows a similar localization effect induced by Ω at a fixed interaction strength U = 2.6D.

We now show a comparison of the experimental results with different theoretical analysis of the model in equation (1). Figure 3a shows a zero-temperature phase diagram obtained from dynamical mean-field theory (DMFT)²¹ for the homogeneous system (V_T = 0) with a uniform 1/3 filling (one atom per site) and an equal number of particles for each flavour. The phase diagram clearly has the same shape as the experimental one, showing that the Hubbard U and the coupling Ω cooperate in driving the system from a metallic phase to a more localized state. Between the standard metal and the Mott phase, we find a region where the degree of correlations (as measured by the quasiparticle weight) is strongly selective, the coupled flavours being much more localized than the uncoupled one. It is evident that both selective and global Mott localization occur at a smaller U if Ω is included.

Fig. 3: Theoretical analysis.

a, DMFT phase diagram for a homogeneous system at T = 0 and 1/3 filling. The points refer to different parameter runs. The boundary between the standard metal and the region of selective correlations marks a sharp crossover where the quasiparticle weight of the coupled flavours drops rapidly to a value smaller than 0.05. b, The crosses show the doublon fraction for the trapped system at U = 2.6D and different Ω/D, obtained from a LDA analysis of the homogeneous DMFT results with the experimental parameters. The points are the experimental data of Fig. 2d (averaging procedure and error bars are explained in the caption of that figure). c, Doublon fraction obtained from DMRG for a 1D trapped system of N = 21 particles at T = 0.

Source data

To connect this effect to the experimentally measured signal, Fig. 3b shows the doublon fraction f_d obtained from the homogeneous DMFT results after a local density approximation (LDA) analysis, to take into account the effect of the harmonic trapping in V_T. The reduction of f_d with increasing Ω is in agreement with the experimental observations reported in Fig. 2. The lack of a quantitative matching with Fig. 2d can be attributed to imperfections in the initial state preparation and to the finite temperature of the experiment, resulting in an average entropy per particle of S/N ≈ 2.5k_B (where k_B is the Boltzmann constant), which is known²⁰ to produce an effect on the double occupancies in a trapped system already at Ω = 0. A comprehensive analysis of finite-temperature effects is presented in the Supplementary Information, showing that thermal fluctuations do explain the discrepancy between experiments and theory, without spoiling the properties of the expected zero-temperature phases. There we also show experimental evidence that the entropy of the system is not appreciably affected by the presence of the Raman coupling, ruling out unwanted heating as a possible cause for the reduction of f_d.

Finally, Fig. 3c shows the result of a zero-temperature DMRG calculation of f_d for a harmonically trapped one-dimensional (1D) system (Supplementary Information). Although quantitative agreement with the experimental data should not be sought (because of the different dimensionality and the finite temperature of the experimental realization), the overall behaviour, that is, a reduction of the doublons for increasing U and Ω, is correctly captured and agrees also with DMFT. This also indicates that the phenomena we are exploring are generic and qualitatively independent from the dimensionality.

In addition to the enhancement of the Mott localization, the DMFT phase diagram of Fig. 3a shows that Ω is expected to result in a flavour-dependent localization of the many-body system. The flavour-selective behaviour can be detected experimentally by resolving the spin character of the doublons, that is, by counting how many atoms form doublons in each of the three pairs $\left|12\right\rangle$, $\left|23\right\rangle$ and $\left|31\right\rangle$ by means of state-selective photoassociation at a high magnetic field (Supplementary Information). Figure 4 shows the quantity γ(12) = N_d(12)/N_d, where N_d(12) is the number of atoms forming doublons in the $\left|12\right\rangle$ channel, as a function of Ω and fixed U = 2.6D. The measured value at Ω = 0 agrees with the expectation for a system with SU(3) symmetry, for which γ(12) = 1/3. As Ω is increased and the SU(3) symmetry is broken, γ(12) diminishes, eventually approaching zero for Ω ≈ D. The doublons acquire a strongly flavour-selective behaviour.

Fig. 4: Evidence of state-selective correlations.

Experimental values of γ(12) as a function of Ω/D for a fixed U = 2.6D. The circles are averages over an interval N = (5–35) × 10³, error bars are obtained from a bootstrap analysis (Supplementary Information) while the colour shade is a guide to the eye. The crosses are obtained from an LDA analysis of the DMFT results. The dashed line shows the expected value for a system with SU(3) symmetry.

Source data

This suppression of $\left|12\right\rangle$ doublons is triggered by the polarization effect in the rotated $\left|\pm \right\rangle$ basis, which can be understood, at a qualitative level, already from the simplified, non-interacting case sketched in Fig. 1c. While $\left|23\right\rangle$ and $\left|31\right\rangle$ doublons can be formed by two fermions in the lowest single-particle states $\left|+\right\rangle$ and $\left|3\right\rangle$, $\left|12\right\rangle$ doublons can be formed only if the two fermions occupy states $\left|+\right\rangle$ and $\left|-\right\rangle$, therefore with an additional energy cost of Ω/2. Interactions then increase this effect¹², leading to strong flavour-selective results even for small values of Ω.

The crosses in Fig. 4 are the result of a DMFT calculation in which the flavour populations are kept equal and the harmonic trapping V_T has been taken into account in an LDA approach. The results of this numerical calculation are in good agreement with the experimental findings, with a larger degree of selectivity for the theoretical calculation. We argue that better agreement could be sought by including finite-temperature effects in the calculation. Indeed, we expect the state-selective behaviour to be reduced by the thermal occupation of higher-energy states, leading to an effective reduction of the polarization in the $\left|+\right\rangle$, $\left|-\right\rangle$ basis.

Note that the experimental observation of a finite number of $\left|12\right\rangle$ doublons at small but finite Ω is an indication of the validity of the protocol used for the preparation of the atomic state, which is different for Ω = 0 and Ω > 0 (Supplementary Information). Note also that, despite the polarization in the dressed $\left|+\right\rangle$, $\left|-\right\rangle$ basis discussed above, we have verified that the populations of the bare states $\left|1\right\rangle$, $\left|2\right\rangle$ and $\left|3\right\rangle$ remain always equal under all the experimental conditions we have considered. This is indeed an important aspect of our experiment. If the populations of the bare states were not fixed (and in particular if N₃ was left free to adapt), the dressed states would be populated according to the scheme in Fig. 1c, leading to N₁ = N₂ > N₃, which favours flavour-selective physics already in the non-interacting system. The experimental state preparation procedure counteracts the trivial differentiation between flavours by forcing an even occupation. Therefore, we conclude that the flavour selectivity that we observed is essentially due to quantum correlations induced by interactions.

In the theoretical DMFT calculations, the equal population constraint is enforced by including an external field h (Supplementary Information) that favours the occupation of $\left|3\right\rangle$ in such a way as to match the experimental condition N₁ + N₂ + N₃ = N/3. Comparing with ref. ¹², where the populations were left free, we observe that the quantum correlations leading to the selective regime survive the inclusion of the field h. In general terms, single-particle effects trigger flavour selectivity, but the inclusion of interactions strongly enhances the differentiation, turning a minor modulation of kinetic energy into a quantitative phenomenon which can also lead to a selective Mott transition²². This is a very general framework, underlying many investigations of multicomponent models.

Exploiting an idealized quantum simulator, we have obtained clear-cut evidence for correlation-induced flavour-selective physics, where the SU(N) symmetry-breaking coupling Ω is only the trigger of a flavour-selective phenomenon which is fundamentally driven by correlation effects. Our realization of multicomponent Hubbard physics with coherent internal couplings opens new paths for the quantum simulation of new classes of materials ranging from high-temperature superconductors to interacting topological insulators as described by the Bernevig–Hughes–Zhang model²³. Once the coupling is realized with a non-zero momentum transfer (that is, non-collinear Raman beams), a full range of possibilities will emerge, including the study of magnetic crystals²⁴, fractional quantum Hall states²⁵ and the effect of interactions of topological phase transitions²⁶ and on the associated edge states²⁷.