Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Interaction-driven breakdown of dynamical localization in a kicked quantum gas

Nature Physics volume 18, pages 1302–1306 (2022)Cite this article

Subjects

A Publisher Correction to this article was published on 04 October 2022

This article has been updated

Abstract

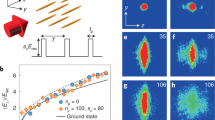
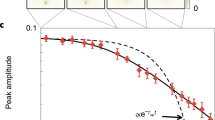
Quantum interference can limit energy absorption in a continually kicked system through a single-particle ergodicity-breaking mechanism known as dynamical localization1,2. The effect of many-body interactions on dynamically localized states, although important to a fundamental understanding of quantum decoherence, has remained unexplored despite more than two decades of experimental studies3,4,5. Here we report the experimental realization of a kicked quantum rotor ensemble with tunable interactions using a Bose–Einstein condensate in a pulsed optical lattice. We observe a clear breakdown of dynamical localization due to interactions, but the resulting dynamics do not restore classical chaotic behaviour, instead displaying sublinear anomalous diffusion. Moreover, echo-type time-reversal experiments establish the role of interactions in destroying reversibility. These results quantitatively elucidate the dynamical transition to many-body quantum chaos and advance our understanding of quantum anomalous diffusion, with implications on the protection of quantum information in interacting driven systems.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Experimentally realizing an interacting QKR.
Fig. 2: Observing the interaction-induced emergence of quantum chaos.
Fig. 3: Effect of interactions on reversibility in echo experiments.

Similar content being viewed by others

Data availability

All data needed to evaluate the conclusions in this study are presented in the Letter and the Supplementary Information.

Code availability

The codes used for data analysis and numerical simulation are available from the corresponding author upon reasonable request.

Change history

References

  1. Fishman, S., Grempel, D. R. & Prange, R. E. Chaos, quantum recurrences, and Anderson localization. Phys. Rev. Lett. 49, 509–512 (1982).

    Article  ADS  MathSciNet  Google Scholar 

  2. Grempel, D. R., Prange, R. E. & Fishman, S. Quantum dynamics of a nonintegrable system. Phys. Rev. A 29, 1639–1647 (1984).

    Article  ADS  Google Scholar 

  3. Moore, F. L., Robinson, J. C., Bharucha, C. F., Sundaram, B. & Raizen, M. G. Atom optics realization of the quantum δ-kicked rotor. Phys. Rev. Lett. 75, 4598–4601 (1995).

    Article  ADS  Google Scholar 

  4. Manai, I. et al. Experimental observation of two-dimensional Anderson localization with the atomic kicked rotor. Phys. Rev. Lett. 115, 240603 (2015).

    Article  ADS  Google Scholar 

  5. Chabé, J. et al. Experimental observation of the Anderson metal-insulator transition with atomic matter waves. Phys. Rev. Lett. 101, 255702 (2008).

    Article  ADS  Google Scholar 

  6. Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015).

    Article  ADS  Google Scholar 

  7. Abanin, D. A., Altman, E., Bloch, I. & Serbyn, M. Colloquium: many-body localization, thermalization, and entanglement. Rev. Mod. Phys. 91, 021001 (2019).

    Article  ADS  MathSciNet  Google Scholar 

  8. Bernien, H. et al. Probing many-body dynamics on a 51-atom quantum simulator. Nature 551, 579–584 (2017).

    Article  ADS  Google Scholar 

  9. Serbyn, M., Abanin, D. A. & Papić, Z. Quantum many-body scars and weak breaking of ergodicity. Nat. Phys. 17, 675–685 (2021).

    Article  Google Scholar 

  10. Singh, K. et al. Quantifying and controlling prethermal nonergodicity in interacting Floquet matter. Phys. Rev. X 9, 041021 (2019).

    Google Scholar 

  11. Rubio-Abadal, A. et al. Floquet prethermalization in a Bose-Hubbard system. Phys. Rev. X 10, 021044 (2020).

    Google Scholar 

  12. Peng, P., Yin, C., Huang, X., Ramanathan, C. & Cappellaro, P. Floquet prethermalization in dipolar spin chains. Nat. Phys. 17, 444–447 (2021).

  13. Langen, T. et al. Experimental observation of a generalized Gibbs ensemble. Science 348, 207–211 (2015).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. Ueda, M. Quantum equilibration, thermalization and prethermalization in ultracold atoms. Nat. Rev. Phys. 2, 669–681 (2020).

    Article  Google Scholar 

  15. Weidinger, S. A. & Knap, M. Floquet prethermalization and regimes of heating in a periodically driven, interacting quantum system. Sci. Rep. 7, 45382 (2017).

    Article  ADS  Google Scholar 

  16. Haake, F., Gnutzmann, S. & Kuś, M. Quantum Signatures of Chaos (Springer, 2018).

  17. Chirikov, B. V. A universal instability of many-dimensional oscillator systems. Phys. Rep. 52, 263–379 (1979).

    Article  ADS  MathSciNet  Google Scholar 

  18. Lemarié, G., Lignier, H., Delande, D., Szriftgiser, P. & Garreau, J. C. Critical state of the Anderson transition: between a metal and an insulator. Phys. Rev. Lett. 105, 090601 (2010).

    Article  ADS  Google Scholar 

  19. Sajjad, R. et al. Observation of the quantum boomerang effect. Phys. Rev. X 12, 011035 (2022).

    Google Scholar 

  20. Shepelyansky, D. L. Delocalization of quantum chaos by weak nonlinearity. Phys. Rev. Lett. 70, 1787–1790 (1993).

    Article  ADS  Google Scholar 

  21. Gligorić, G., Bodyfelt, J. D. & Flach, S. Interactions destroy dynamical localization with strong and weak chaos. Europhys. Lett. 96, 30004 (2011).

  22. Lellouch, S., Rançon, A., De Bi’evre, S., Delande, D. & Garreau, J. C. Dynamics of the mean-field-interacting quantum kicked rotor. Phys. Rev. A 101, 043624 (2020).

    Article  ADS  Google Scholar 

  23. Pikovsky, A. S. & Shepelyansky, D. L. Destruction of Anderson localization by a weak nonlinearity. Phys. Rev. Lett. 100, 094101 (2008).

    Article  ADS  Google Scholar 

  24. Flach, S., Krimer, D. O. & Skokos, C. Universal spreading of wave packets in disordered nonlinear systems. Phys. Rev. Lett. 102, 024101 (2009).

    Article  ADS  Google Scholar 

  25. Notarnicola, S. et al. From localization to anomalous diffusion in the dynamics of coupled kicked rotors. Phys. Rev. E 97, 022202 (2018).

    Article  ADS  Google Scholar 

  26. Keser, A. C., Ganeshan, S., Refael, G. & Galitski, V. Dynamical many-body localization in an integrable model. Phys. Rev. B 94, 085120 (2016).

    Article  ADS  Google Scholar 

  27. Rylands, C., Rozenbaum, E. B., Galitski, V. & Konik, R. Many-body dynamical localization in a kicked Lieb-Liniger gas. Phys. Rev. Lett. 124, 155302 (2020).

    Article  ADS  MathSciNet  Google Scholar 

  28. Ammann, H., Gray, R., Shvarchuck, I. & Christensen, N. Quantum delta-kicked rotor: experimental observation of decoherence. Phys. Rev. Lett. 80, 4111–4115 (1998).

    Article  ADS  Google Scholar 

  29. Klappauf, B. G., Oskay, W. H., Steck, D. A. & Raizen, M. G. Observation of noise and dissipation effects on dynamical localization. Phys. Rev. Lett. 81, 1203–1206 (1998).

    Article  ADS  Google Scholar 

  30. Gadway, B., Reeves, J., Krinner, L. & Schneble, D. Evidence for a quantum-to-classical transition in a pair of coupled quantum rotors. Phys. Rev. Lett. 110, 190401 (2013).

    Article  ADS  Google Scholar 

  31. Oskay, W. H., Steck, D. A. & Raizen, M. G. Timing noise effects on dynamical localization. Chaos Soliton. Fract. 16, 409–416 (2003).

    Article  MATH  Google Scholar 

  32. Norrie, A. A., Ballagh, R. J. & Gardiner, C. W. Quantum turbulence and correlations in Bose-Einstein condensate collisions. Phys. Rev. A 73, 043617 (2006).

    Article  ADS  Google Scholar 

  33. Deuar, P. & Drummond, P. D. Correlations in a BEC collision: first-principles quantum dynamics with 150,000 atoms. Phys. Rev. Lett. 98, 120402 (2007).

    Article  ADS  Google Scholar 

  34. Vuatelet, V. & Rançon, A. Effective thermalization of a many-body dynamically localized Bose gas. Phys. Rev. A. 104, 043302 (2021).

    Article  ADS  Google Scholar 

  35. Rozenbaum, E. B., Ganeshan, S. & Galitski, V. Lyapunov exponent and out-of-time-ordered correlator’s growth rate in a chaotic system. Phys. Rev. Lett. 118, 086801 (2017).

    Article  ADS  Google Scholar 

  36. Gorin, T., Prosen, T., Seligman, T. H. & Žnidarič, M. Dynamics of Loschmidt echoes and fidelity decay. Phys. Rep. 435, 33–156 (2006).

    Article  ADS  Google Scholar 

  37. Ullah, A. & Hoogerland, M. D. Experimental observation of Loschmidt time reversal of a quantum chaotic system. Phys. Rev. E 83, 046218 (2011).

    Article  ADS  Google Scholar 

  38. Martin, J., Georgeot, B. & Shepelyansky, D. L. Cooling by time reversal of atomic matter waves. Phys. Rev. Lett. 100, 044106 (2008).

    Article  ADS  Google Scholar 

  39. Lepers, M., Zehnlé, V. & Garreau, J. C. Kicked-rotor quantum resonances in position space. Phys. Rev. A 77, 043628 (2008).

    Article  ADS  Google Scholar 

  40. Swingle, B., Bentsen, G., Schleier-Smith, M. & Hayden, P. Measuring the scrambling of quantum information. Phys. Rev. A 94, 040302 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  41. Toh, J. H. S. et al. Observation of many-body dynamical delocalization in a kicked ultracold gas. Preprint at http://128.84.4.18/abs/2106.13773 (2021).

  42. Pollack, S. E. et al. Extreme tunability of interactions in a 7Li Bose-Einstein condensate. Phys. Rev. Lett. 102, 090402 (2009).

    Article  ADS  Google Scholar 

  43. Tenart, A. et al. Two-body collisions in the time-of-flight dynamics of lattice Bose superfluids. Phys. Rev. Res. 2, 013017 (2020).

    Article  Google Scholar 

Download references

Acknowledgements

We acknowledge helpful conversations with A. Rançon, N. Yao and T. Schuster. Funding: D.M.W. acknowledges support from the Air Force Office of Scientific Research (AFOSR FA9550-20-1-0240), the Army Research Office (ARO PECASE W911NF1410154) and the National Science Foundation (NSF CAREER 1555313 and QLCI OMA-2016245). D.M.W., R.S. and E.N.-M. acknowledge support from the UCSB NSF Quantum Foundry through the Q-AMASE-i program (grant no. DMR-1906325). V.G. was supported by US ARO contract no. W911NF1310172, NSF DMR-2037158 and the Simons Foundation.

Author information

Authors and Affiliations

  1. Department of Physics, University of California, Santa Barbara, CA, USA

    Alec Cao, Roshan Sajjad, Hector Mas, Ethan Q. Simmons, Jeremy L. Tanlimco, Eber Nolasco-Martinez, Toshihiko Shimasaki, H. Esat Kondakci & David M. Weld

  2. Joint Quantum Institute and Condensed Matter Theory Center, University of Maryland, College Park, MD, USA

    Victor Galitski

Authors
  1. Alec Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Roshan Sajjad
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hector Mas
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ethan Q. Simmons
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jeremy L. Tanlimco
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Eber Nolasco-Martinez
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Toshihiko Shimasaki
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. H. Esat Kondakci
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Victor Galitski
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. David M. Weld
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.C., R.S., H.M., E.Q.S., J.L.T., E.N.-M., T.S. and H.E.K. contributed to operate the experiment and perform the measurements. A.C., R.S. and H.M. analysed the data. A.C. conceptualized and performed the theoretical simulations of the rotor and spin models. V.G. and D.M.W. developed the idea for the experiment. D.M.W. supervised the work. A.C., R.S., H.M., V.G. and D.M.W. wrote the manuscript. All the authors contributed to the discussion and interpretation of the results.

Corresponding author

Correspondence to David M. Weld.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Jakub Zakrzewski, Maarten Hoogerland and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Figs. 1–8 and Sections 1–7.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cao, A., Sajjad, R., Mas, H. et al. Interaction-driven breakdown of dynamical localization in a kicked quantum gas. Nat. Phys. 18, 1302–1306 (2022). https://doi.org/10.1038/s41567-022-01724-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01724-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing