Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Realizing coherently convertible dual-type qubits with the same ion species

Nature Physics volume 18, pages 1058–1061 (2022)Cite this article

Subjects

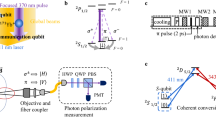
Abstract

Trapped ions constitute one of the most promising systems for implementing quantum computing and networking1,2. For large-scale ion-trap-based quantum computers and networks, it is critical to have two types of qubit: one for computation and storage, and another for auxiliary operations such as qubit detection3, sympathetic cooling4,5,6,7 and entanglement generation through photon links8,9. Although the two qubit types can be implemented using two different ion species3,10,11,12,13, this approach introduces substantial complexity into creating and controlling each qubit type14,15. Here we resolve these challenges by implementing two coherently convertible qubit types using one ion species. We encode the qubits into two pairs of clock states of the 171Yb+ ions, and achieve microsecond-level conversion rates between the two types with one-way fidelities of 99.5%. We further demonstrate that operations on one qubit type, including sympathetic laser cooling, single-qubit gates and qubit detection, have crosstalk errors less than 0.06% on the other type, which is below the best-known error threshold of ~1% for fault-tolerant quantum computing using the surface code1,16. Our work establishes the feasibility and advantages of using coherently convertible dual-type qubits with the same ion species for large-scale quantum computing and networking.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Schematic of the experiment.
Fig. 2: Coherent conversion between the two qubit types.
Fig. 3: Crosstalk error of S-qubit operations on the F-qubit.
Fig. 4: Sympathetic cooling and crosstalk error.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the authors upon request. Source data are provided with this Paper.

References

  1. Nielsen, M. & Chuang, I. Quantum Computation and Quantum Information 10th anniversary edn (Cambridge Univ. Press, 2010).

  2. Monroe, C. & Kim, J. Scaling the ion trap quantum processor. Science 339, 1164–1169 (2013).

    Article  ADS  Google Scholar 

  3. Negnevitsky, V. et al. Repeated multi-qubit readout and feedback with a mixed-species trapped-ion register. Nature 563, 527–531 (2018).

    Article  ADS  Google Scholar 

  4. Rohde, H. et al. Sympathetic ground-state cooling and coherent manipulation with two-ion crystals. J. Opt. B Quantum Semiclassical Opt. 3, S34–S41 (2001).

    Article  Google Scholar 

  5. Blinov, B. B. et al. Sympathetic cooling of trapped Cd+ isotopes. Phys. Rev. A 65, 040304 (2002).

    Article  ADS  Google Scholar 

  6. Barrett, M. D. et al. Sympathetic cooling of 9Be+ and 24Mg+ for quantum logic. Phys. Rev. A 68, 042302 (2003).

    Article  ADS  Google Scholar 

  7. Home, J. P. et al. Memory coherence of a sympathetically cooled trapped-ion qubit. Phys. Rev. A 79, 050305 (2009).

    Article  ADS  Google Scholar 

  8. Duan, L.-M. & Monroe, C. Colloquium: Quantum networks with trapped ions. Rev. Mod. Phys. 82, 1209–1224 (2010).

    Article  ADS  Google Scholar 

  9. Hucul, D. et al. Modular entanglement of atomic qubits using photons and phonons. Nat. Phys. 11, 37–42 (2015).

    Article  Google Scholar 

  10. Tan, T. R. et al. Multi-element logic gates for trapped-ion qubits. Nature 528, 380–383 (2015).

    Article  ADS  Google Scholar 

  11. Inlek, I. V., Crocker, C., Lichtman, M., Sosnova, K. & Monroe, C. Multispecies trapped-ion node for quantum networking. Phys. Rev. Lett. 118, 250502 (2017).

    Article  ADS  Google Scholar 

  12. Bruzewicz, C., McConnell, R., Stuart, J., Sage, J. & Chiaverini, J. Dual-species, multi-qubit logic primitives for Ca+/Sr+ trapped-ion crystals. npj Quantum Inf. 5, 102 (2019).

    Article  ADS  Google Scholar 

  13. Wan, Y. et al. Quantum gate teleportation between separated qubits in a trapped-ion processor. Science 364, 875–878 (2019).

    Article  ADS  Google Scholar 

  14. Sosnova, K., Carter, A. & Monroe, C. Character of motional modes for entanglement and sympathetic cooling of mixed-species trapped-ion chains. Phys. Rev. A 103, 012610 (2021).

    Article  ADS  Google Scholar 

  15. Lin, G.-D. & Duan, L.-M. Sympathetic cooling in a large ion crystal. Quantum Inf. Process. 15, 5299–5313 (2016).

    Article  ADS  Google Scholar 

  16. Campbell, E. T., Terhal, B. M. & Vuillot, C. Roads towards fault-tolerant universal quantum computation. Nature 549, 172–179 (2017).

    Article  ADS  Google Scholar 

  17. Gottesman, D. Theory of fault-tolerant quantum computation. Phys. Rev. A 57, 127–137 (1998).

    Article  ADS  Google Scholar 

  18. Duan, L.-M., Blinov, B. B., Moehring, D. L. & Monroe, C. Scalable trapped ion quantum computation with a probabilistic ion-photon mapping. Quantum Info Comput. 4, 165–173 (2004).

    MathSciNet  MATH  Google Scholar 

  19. Monroe, C. et al. Large-scale modular quantum-computer architecture with atomic memory and photonic interconnects. Phys. Rev. A 89, 022317 (2014).

    Article  ADS  Google Scholar 

  20. Zhu, S.-L., Monroe, C. & Duan, L.-M. Trapped ion quantum computation with transverse phonon modes. Phys. Rev. Lett. 97, 050505 (2006).

    Article  ADS  Google Scholar 

  21. Lin, G.-D. et al. Large-scale quantum computation in an anharmonic linear ion trap. Europhys. Lett. 86, 60004 (2009).

    Article  ADS  Google Scholar 

  22. Taylor, P., Roberts, M., Barwood, G. P. & Gill, P. Combined optical-infrared single-ion frequency standard. Opt. Lett. 23, 298–300 (1998).

    Article  ADS  Google Scholar 

  23. Leibfried, D., Blatt, R., Monroe, C. & Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 75, 281–324 (2003).

    Article  ADS  Google Scholar 

  24. Roman, C., Ransford, A., Ip, M. & Campbell, W. C. Coherent control for qubit state readout. N. J. Phys. 22, 073038 (2020).

    Article  Google Scholar 

  25. Edmunds, C. L. et al. Scalable hyperfine qubit state detection via electron shelving in the 2D5/2 and 2F7/2 manifolds in 171Yb+. Phys. Rev. A 104, 012606 (2021).

    Article  ADS  Google Scholar 

  26. Christensen, J. E., Hucul, D., Campbell, W. C. & Hudson, E. R. High-fidelity manipulation of a qubit enabled by a manufactured nucleus. npj Quantum Inf. 6, 35 (2020).

    Article  ADS  Google Scholar 

  27. Barreiro, J. T. et al. An open-system quantum simulator with trapped ions. Nature 470, 486–491 (2011).

    Article  ADS  Google Scholar 

  28. Monz, T. et al. Realization of a scalable Shor algorithm. Science 351, 1068–1070 (2016).

    Article  ADS  MathSciNet  Google Scholar 

  29. Piltz, C., Sriarunothai, T., Ivanov, S. S., Wölk, S. & Wunderlich, C. Versatile microwave-driven trapped ion spin system for quantum information processing. Sci. Adv. 2, e1600093 (2016).

    Article  ADS  Google Scholar 

  30. Olmschenk, S. et al. Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007).

    Article  ADS  Google Scholar 

  31. Wootters, W. K. & Fields, B. D. Optimal state-determination by mutually unbiased measurements. Ann. Phys. 191, 363–381 (1989).

    Article  ADS  MathSciNet  Google Scholar 

  32. Klappenecker, A. & Rotteler, M. Mutually unbiased bases are complex projective 2-designs. In Proc. International Symposium on Information Theory, 2005 1740–1744 (IEEE, 2005).

  33. Choi, T. et al. Optimal quantum control of multimode couplings between trapped ion qubits for scalable entanglement. Phys. Rev. Lett. 112, 190502 (2014).

    Article  ADS  Google Scholar 

  34. Brown, K. R., Harrow, A. W. & Chuang, I. L. Arbitrarily accurate composite pulse sequences. Phys. Rev. A 70, 052318 (2004).

    Article  ADS  Google Scholar 

  35. Magesan, E., Gambetta, J. M. & Emerson, J. Scalable and robust randomized benchmarking of quantum processes. Phys. Rev. Lett. 106, 180504 (2011).

    Article  ADS  Google Scholar 

  36. Feng, L. et al. Efficient ground-state cooling of large trapped-ion chains with an electromagnetically-induced-transparency tripod scheme. Phys. Rev. Lett. 125, 053001 (2020).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the Tsinghua University Initiative Scientific Research Program and the Ministry of Education of China through its fund to the IIIS.

Author information

Author notes

  1. These authors contributed equally: H.-X. Yang, J.-Y. Ma.

Authors and Affiliations

  1. Center for Quantum Information, Institute for Interdisciplinary Information Sciences, Tsinghua University, Beijing, China

    H.-X. Yang, J.-Y. Ma, Y.-K. Wu, Y. Wang, M.-M. Cao, W.-X. Guo, Y.-Y. Huang, L. Feng, Z.-C. Zhou & L.-M. Duan

Authors
  1. H.-X. Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J.-Y. Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Y.-K. Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Y. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. M.-M. Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. W.-X. Guo
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Y.-Y. Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. L. Feng
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Z.-C. Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. L.-M. Duan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

L.-M.D. proposed and supervised the experiment. H.-X.Y., J.-Y.M., Y.W., M.-M.C., W.-X.G., Y.-Y.H., L.F., Y.-K.W. and Z.-C.Z. carried out the experiment. H.-X.Y., J.-Y.M., Y.-K.W. and L.-M.D. wrote the manuscript.

Corresponding author

Correspondence to L.-M. Duan.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Cornelius Hempel and Christof Wunderlich for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Detailed time sequence for measuring the crosstalk of S-qubit operations on the F-qubit.

Detailed time sequence for measuring the crosstalk of S-qubit operations on the F-qubit. a, Time sequence for the S-qubit and the F-qubit (which also starts from an S-qubit). During the verification step of the F-qubit, resonant 370-nm laser is applied, so the S-qubit needs to be reinitialized after that. b, Specific S-qubit operations for Fig. 3b to measure crosstalk errors of Raman Rabi oscillation using 355-nm laser. c, Specific S-qubit operations for Fig. 3c to measure crosstalk errors of preparation and detection of \(\left|0\right\rangle\). d, Specific S-qubit operations for Fig. 3d to measure crosstalk errors of preparation and detection of \(\left|1\right\rangle\).

Extended Data Fig. 2 Carrier Rabi oscillation of the 411-nm laser and 3,432-nm laser.

Carrier Rabi oscillation of a, the 411-nm laser and b, 3,432-nm laser. The 411-nm laser has an optical power of about 0.8 mW and a beam diameter of about 8 µm, which generates a Rabi frequency of about 2π × 859.4 kHz. The 3,432-nm laser has an optical power of about 0.5 mW and a beam diameter of about 73 µm, which gives a Rabi frequency of about 2π × 1.2 MHz.

Source data

Extended Data Fig. 3 Randomized benchmarking of the microwave-driven single-qubit gates.

Randomized benchmarking of the microwave-driven single-qubit gates for a, the S-qubit and b, the F-qubit. The average gate fidelity is (99.98 ± 0.04)% for the S-qubit and (99.99 ± 0.04)% for the F-qubit.

Source data

Extended Data Fig. 4 Carrier Rabi oscillation of 411-nm laser after 500 µs sympathetic cooling.

Carrier Rabi oscillation of 411-nm laser after 500 µs sympathetic cooling. The fitted effective temperature is (9.2 ± 0.2) mK.

Source data

Source data

Source Data Fig. 2

Statistical source data.

Source Data Fig. 3

Statistical source data.

Source Data Fig. 4

Statistical source data.

Source Data Extended Data Fig. 2

Statistical source data.

Source Data Extended Data Fig. 3

Statistical source data.

Source Data Extended Data Fig. 4

Statistical source data.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, HX., Ma, JY., Wu, YK. et al. Realizing coherently convertible dual-type qubits with the same ion species. Nat. Phys. 18, 1058–1061 (2022). https://doi.org/10.1038/s41567-022-01661-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01661-5

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing