Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Parity measurement in the strong dispersive regime of circuit quantum acoustodynamics

Nature Physics volume 18, pages 794–799 (2022)Cite this article

Subjects

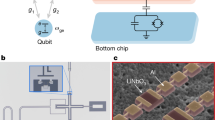
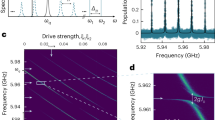
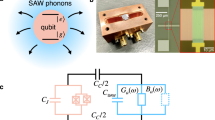
Abstract

Mechanical resonators are emerging as an important new platform for quantum science and technologies. A large number of proposals for using them to store, process and transduce quantum information motivates the development of increasingly sophisticated techniques for controlling mechanical motion in the quantum regime. By interfacing mechanical resonators with superconducting circuits, circuit quantum acoustodynamics can make a variety of important tools available for manipulating and measuring motional quantum states. Here we demonstrate the direct measurements of phonon number distribution and parity of non-classical mechanical states. We do this by operating our system in the strong dispersive regime, where a superconducting qubit can be used to spectroscopically resolve the phonon Fock states. These measurements are some of the basic building blocks for constructing acoustic quantum memories and processors. Furthermore, our results open the door for performing even more complex quantum algorithms using mechanical systems, such as quantum error correction and multimode operations.

This is a preview of subscription content, access via your institution

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Characterization of the ℏBAR device.
Fig. 2: Dispersive measurement of phonon coherent states.
Fig. 3: Dispersive measurement of phonon Fock states.
Fig. 4: Wigner tomography of non-classical phonon states.

Data availability

Source data are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.

Code availability

Analysis and simulation codes that support the findings of this study are available from the corresponding authors upon reasonable request.

References

  1. Chu, Y. et al. Creation and control of multi-phonon Fock states in a bulk acoustic-wave resonator. Nature 563, 666–670 (2018).

    Article  ADS  Google Scholar 

  2. Bienfait, A. et al. Quantum erasure using entangled surface acoustic phonons. Phys. Rev. X 10, 021055 (2020).

  3. Arrangoiz-Arriola, P. et al. Resolving the energy levels of a nanomechanical oscillator. Nature 571, 537–540 (2019).

    Article  ADS  Google Scholar 

  4. Sletten, L. R., Moores, B. A., Viennot, J. J. & Lehnert, K. W. Resolving phonon Fock states in a multimode cavity with a double-slit qubit. Phys. Rev. X 9, 021056 (2019).

    Google Scholar 

  5. Kotler, S. et al. Direct observation of deterministic macroscopic entanglement. Science 372, 622–625 (2021).

    Article  ADS  Google Scholar 

  6. Ockeloen-Korppi, C. F. et al. Stabilized entanglement of massive mechanical oscillators. Nature 556, 478–482 (2018).

    Article  ADS  Google Scholar 

  7. MacCabe, G. S. et al. Nano-acoustic resonator with ultralong phonon lifetime. Science 370, 840–843 (2020).

    Article  ADS  Google Scholar 

  8. Tsaturyan, Y., Barg, A., Polzik, E. S. & Schliesser, A. Ultracoherent nanomechanical resonators via soft clamping and dissipation dilution. Nat. Nanotechnol. 12, 776–783 (2017).

    Article  Google Scholar 

  9. Chamberland, C. et al. Building a fault-tolerant quantum computer using concatenated cat codes. PRX Quantum 3, 010329 (2022).

  10. Pikovski, I., Vanner, M. R., Aspelmeyer, M., Kim, M. S. & Brukner, Č. Probing Planck-scale physics with quantum optics. Nat. Phys. 8, 393–397 (2012).

    Article  Google Scholar 

  11. Bertet, P. et al. Direct measurement of the Wigner function of a one-photon Fock state in a cavity. Phys. Rev. Lett. 89, 200402 (2002).

    Article  ADS  Google Scholar 

  12. Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007).

    Article  ADS  Google Scholar 

  13. Walter, T. et al. Rapid high-fidelity single-shot dispersive readout of superconducting qubits. Phys. Rev. Appl. 7, 054020 (2017).

    Article  ADS  Google Scholar 

  14. Rosenblum, S. et al. Fault-tolerant detection of a quantum error. Science 361, 266–270 (2018).

    Article  ADS  MathSciNet  Google Scholar 

  15. Ofek, N. et al. Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441–445 (2016).

    Article  ADS  Google Scholar 

  16. Hu, L. et al. Quantum error correction and universal gate set operation on a binomial bosonic logical qubit. Nat. Phys. 15, 503–508 (2019).

    Article  Google Scholar 

  17. Chu, Y. & Gröblacher, S. A perspective on hybrid quantum opto- and electromechanical systems. Appl. Phys. Lett. 117, 150503 (2020).

  18. Chu, Y. et al. Quantum acoustics with superconducting qubits. Science 358, 199–202 (2017).

    Article  ADS  MathSciNet  Google Scholar 

  19. Satzinger, K. J. et al. Simple non-galvanic flip-chip integration method for hybrid quantum systems. Appl. Phys. Lett. 114, 173501 (2019).

    Article  ADS  Google Scholar 

  20. Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 062320 (2004).

    Article  ADS  Google Scholar 

  21. Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007).

  22. Krantz, P. et al. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 6, 021318 (2019).

    Article  ADS  Google Scholar 

  23. Blais, A., Grimsmo, A. L., Girvin, S. M. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).

    Article  ADS  MathSciNet  Google Scholar 

  24. Sun, L. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444–448 (2014).

    Article  ADS  Google Scholar 

  25. Royer, A. Wigner function as the expectation value of a parity operator. Phys. Rev. A 15, 449–450 (1977).

    Article  ADS  MathSciNet  Google Scholar 

  26. Burnett, J. J. et al. Decoherence benchmarking of superconducting qubits. npj Quantum Inf. 5, 54 (2019).

    Article  Google Scholar 

  27. Johansson, J. R., Nation, P. D. & Nori, F. QuTiP: an open-source Python framework for the dynamics of open quantum systems. Comput. Phys. Commun. 183, 1760–1772 (2012).

    Article  ADS  Google Scholar 

  28. Pechal, M., Arrangoiz-Arriola, P. & Safavi-Naeini, A. H. Superconducting circuit quantum computing with nanomechanical resonators as storage. Quantum Sci. Technol. 4, 015006 (2019).

    Article  ADS  Google Scholar 

  29. Hann, C. T. et al. Hardware-efficient quantum random access memory with hybrid quantum acoustic systems. Phys. Rev. Lett. 123, 250501 (2019).

    Article  ADS  Google Scholar 

  30. McCormick, K. C. et al. Quantum-enhanced sensing of a single-ion mechanical oscillator. Nature 572, 86–90 (2019).

    Article  ADS  Google Scholar 

  31. Penrose, R. On gravity’s role in quantum state reduction. Gen. Relat. Gravit. 28, 581–600 (1996).

    Article  ADS  MathSciNet  Google Scholar 

  32. Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 342, 607–610 (2013).

    Article  ADS  MathSciNet  Google Scholar 

  33. Heeres, R. W. et al. Implementing a universal gate set on a logical qubit encoded in an oscillator. Nat. Commun. 8, 94 (2017).

    Article  ADS  Google Scholar 

  34. Gao, Y. Y. et al. Entanglement of bosonic modes through an engineered exchange interaction. Nature 566, 509–512 (2019).

    Article  ADS  Google Scholar 

  35. Leghtas, Z. et al. Confining the state of light to a quantum manifold by engineered two-photon loss. Science 347, 853–857 (2015).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank X. Cao and A. deMello for help with the flip-chip-bonding process and J.-C. Besse for help with the qubit fabrication. We thank B. Li for providing support with the QuTiP simulations. The fabrication of devices was performed at the FIRST cleanroom of ETH Zürich and the BRNC cleanroom of IBM Zürich. M.F. acknowledge The Branco Weiss Fellowship—Society in Science, administered by the ETH Zürich.

Author information

Author notes

  1. These authors contributed equally: Uwe von Lüpke, Yu Yang, Marius Bild.

Authors and Affiliations

  1. Department of Physics, ETH Zürich, Zurich, Switzerland

    Uwe von Lüpke, Yu Yang, Marius Bild, Laurent Michaud, Matteo Fadel & Yiwen Chu

  2. Quantum Center, ETH Zürich, Zurich, Switzerland

    Uwe von Lüpke, Yu Yang, Marius Bild, Laurent Michaud, Matteo Fadel & Yiwen Chu

Authors
  1. Uwe von Lüpke
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yu Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Marius Bild
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Laurent Michaud
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Matteo Fadel
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Yiwen Chu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

U.v.L. and L.M. designed and fabricated the device. U.v.L. and M.B. constructed the parametric amplifier used for the qubit readout. M.B. wrote the experiment control software. Y.Y., U.v.L. and M.B. performed the experiment and analysed the data. Y.Y. performed the QuTiP simulations of the experiment. M.F., M.B. and Y.C. performed the theoretical calculations. Y.C. supervised the work. U.v.L., Y.Y., M.B., M.F. and Y.C. wrote the manuscript.

Corresponding authors

Correspondence to Uwe von Lüpke or Yiwen Chu.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Supplementary Table 1, Figs. 1–6 and Sections A–G.

Source data

Source Data Fig. 1

Source data for Fig. 1d.

Source Data Fig. 2

Source data for Fig. 2 (one tab for each subfigure).

Source Data Fig. 3

Source ata for Fig. 3 (one tab for each subfigure).

Source Data Fig. 4

Source ata for Fig. 4d.

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

von Lüpke, U., Yang, Y., Bild, M. et al. Parity measurement in the strong dispersive regime of circuit quantum acoustodynamics. Nat. Phys. 18, 794–799 (2022). https://doi.org/10.1038/s41567-022-01591-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01591-2

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing