Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

Correlated Hofstadter spectrum and flavour phase diagram in magic-angle twisted bilayer graphene

Nature Physics volume 18, pages 825–831 (2022)Cite this article

Subjects

Abstract

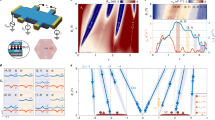
In magic-angle twisted bilayer graphene, the moiré superlattice potential gives rise to narrow electronic bands that support a multitude of many-body quantum phases. Further richness arises in the presence of a perpendicular magnetic field, where the interplay between moiré and magnetic length scales leads to fractal Hofstadter subbands. In this strongly correlated Hofstadter platform, multiple experiments have identified gapped topological and correlated states, but little is known about the phase transitions between them in the intervening compressible regimes. Here we simultaneously unveil sequences of broken-symmetry Chern insulators and resolve sharp phase transitions between competing states with different topological quantum numbers and different occupations of the spin-valley flavour. Our measurements determine the energy spectrum of interacting Hofstadter subbands in magic-angle twisted bilayer graphene and map out the phase diagram of flavour occupancy. In addition, we observe full lifting of the degeneracy of the zeroth Landau levels together with level crossings, indicating moiré valley splitting. We propose a unified flavour polarization mechanism to understand the intricate interplay of topology, interactions and symmetry breaking as a function of density and applied magnetic field in this system.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Device geometry and local electronic compressibility of MATBG.
Fig. 2: Flavour polarization and correlated Hofstadter spectrum.
Fig. 3: First-order phase transitions and flavour phase diagram.
Fig. 4: zLLs and moiré valley polarization.

Similar content being viewed by others

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.

Code availability

The codes that support the findings of this study are available from the corresponding author upon reasonable request.

References

  1. Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).

    ADS  Google Scholar 

  2. Cao, Y. et al. Correlated insulator behavior at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).

    ADS  Google Scholar 

  3. Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).

    ADS  Google Scholar 

  4. Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).

    ADS  Google Scholar 

  5. Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).

    ADS  Google Scholar 

  6. Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).

    ADS  Google Scholar 

  7. Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).

    ADS  Google Scholar 

  8. Cao, Y. et al. Nematicity and competing orders in superconducting magic-angle graphene. Science 372, 264–271 (2021).

    ADS  Google Scholar 

  9. Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).

    ADS  Google Scholar 

  10. Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).

    ADS  Google Scholar 

  11. Saito, Y. et al. Isospin Pomeranchuk effect in twisted bilayer graphene. Nature 592, 220–224 (2021).

    ADS  Google Scholar 

  12. Rozen, A. et al. Entropic evidence for a Pomeranchuk effect in magic-angle graphene. Nature 592, 214–219 (2021).

    ADS  Google Scholar 

  13. Saito, Y. et al. Hofstadter subband ferromagnetism and symmetry-broken Chern insulators in twisted bilayer graphene. Nat. Phys. 17, 478–481 (2021).

    Google Scholar 

  14. Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Flavour Hund’s coupling, Chern gaps and charge diffusivity in moiré graphene. Nature 592, 43–48 (2021).

    Google Scholar 

  15. Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).

    ADS  Google Scholar 

  16. Choi, Y. et al. Correlation-driven topological phases in magic-angle twisted bilayer graphene. Nature 589, 536–541 (2021).

    ADS  Google Scholar 

  17. Das, I. et al. Symmetry-broken Chern insulators and Rashba-like Landau-level crossings in magic-angle bilayer graphene. Nat. Phys. https://doi.org/10.1038/s41567-021-01186-3 (2021).

    Article  Google Scholar 

  18. Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators, van Hove singularities and topological flat bands in magic-angle twisted bilayer graphene. Nat. Mater. 20, 488–494 (2021).

    ADS  Google Scholar 

  19. Tomarken, S. L. et al. Electronic compressibility of magic-angle graphene superlattices. Phys. Rev. Lett. 123, 046601 (2019).

    ADS  Google Scholar 

  20. Pierce, A. et al. Unconventional sequence of correlated Chern insulators in magic-angle twisted bilayer graphene. Nat. Phys. 17, 1210–1215 (2021).

    Google Scholar 

  21. Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).

    ADS  Google Scholar 

  22. Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).

    ADS  Google Scholar 

  23. Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).

    ADS  Google Scholar 

  24. Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019).

    Google Scholar 

  25. Saito, Y., Ge, J., Watanabe, K., Taniguchi, T. & Young, A. F. Independent superconductors and correlated insulators in twisted bilayer graphene. Nat. Phys. 16, 926–930 (2020).

    Google Scholar 

  26. Stepanov, P. et al. Untying the insulating and superconducting orders in magic-angle graphene. Nature 583, 375–378 (2020).

    ADS  Google Scholar 

  27. Liu, X. et al. Tuning electron correlation in magic-angle twisted bilayer graphene using Coulomb screening. Science 371, 1261–1265 (2021).

    ADS  Google Scholar 

  28. Stepanov, P. et al. Competing zero-field Chern insulators in superconducting twisted bilayer graphene. Phys. Rev. Lett. 127, 197701 (2021).

    ADS  Google Scholar 

  29. Po, H. C., Zou, L., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).

    Google Scholar 

  30. Bultinck, N. et al. Ground state and hidden symmetry of magic-angle graphene at even integer filling. Phys. Rev. X 10, 031034 (2020).

    Google Scholar 

  31. Kang, J. & Vafek, O. Strong coupling phases of partially filled twisted bilayer graphene narrow bands. Phys. Rev. Lett. 122, 246401 (2019).

    ADS  Google Scholar 

  32. Liu, J., Liu, J. & Dai, X. Pseudo Landau level representation of twisted bilayer graphene: band topology and implications on the correlated insulating phase. Phys. Rev. B 99, 155415 (2019).

    ADS  Google Scholar 

  33. Lian, B. et al. Twisted bilayer graphene. IV. Exact insulator ground states and phase diagram. Phys. Rev. B 103, 205414 (2021).

    ADS  Google Scholar 

  34. Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976).

    ADS  Google Scholar 

  35. Bistritzer, R. & MacDonald, A. H. Moiré butterflies in twisted bilayer graphene. Phys. Rev. B 84, 035440 (2011).

    ADS  Google Scholar 

  36. Moon, P. & Koshino, M. Energy spectrum and quantum Hall effect in twisted bilayer graphene. Phys. Rev. B 85, 195458 (2012).

    ADS  Google Scholar 

  37. Hejazi, K., Liu, C. & Balents, L. Landau levels in twisted bilayer graphene and semiclassical orbits. Phys. Rev. B 100, 035115 (2019).

    ADS  Google Scholar 

  38. Zhang, Y.-H., Po, H. C. & Senthil, T. Landau level degeneracy in twisted bilayer graphene: role of symmetry breaking. Phys. Rev. B 100, 125104 (2019).

    ADS  Google Scholar 

  39. Lian, B., Xie, F. & Bernevig, B. A. Landau level of fragile topology. Phys. Rev. B 102, 041402 (2020).

    ADS  Google Scholar 

  40. Wannier, G. H. A result not dependent on rationality for Bloch electrons in a magnetic field. Phys. Status Solidi B 88, 757–765 (1978).

    ADS  Google Scholar 

  41. Uri, A. et al. Mapping the twist-angle disorder and Landau levels in magic-angle graphene. Nature 581, 47–52 (2020).

    ADS  Google Scholar 

  42. Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Negative compressibility of interacting two-dimensional electron and quasiparticle gases. Phys. Rev. Lett. 68, 674–677 (1992).

    ADS  Google Scholar 

  43. Zhou, H. et al. Half-and quarter-metals in rhombohedral trilayer graphene. Nature 598, 429–433 (2021).

    ADS  Google Scholar 

  44. Arora, H. S. et al. Superconductivity in metallic twisted bilayer graphene stabilized by WSe2. Nature 583, 379–384 (2020).

    ADS  Google Scholar 

  45. Bi, Z., Yuan, N. F. Q. & Fu, L. Designing flat bands by strain. Phys. Rev. B 100, 035448 (2019).

    ADS  Google Scholar 

  46. Parker, D. E., Soejima, T., Hauschild, J., Zaletel, M. P. & Bultinck, N. Strain-induced quantum phase transitions in magic-angle graphene. Phys. Rev. Lett. 127, 027601 (2021).

    ADS  Google Scholar 

  47. Huang, K. S., Han, Z., Kivelson, S. A. & Yao, H. Pair-density-wave in the strong coupling limit of the Holstein–Hubbard model. npj Quantum Mater. 7, 17 (2022).

    ADS  Google Scholar 

  48. Kang, J., Bernevig, B. A. & Vafek, O. Cascades between light and heavy fermions in the normal state of magic angle twisted bilayer graphene. Preprint at https://arxiv.org/abs/2104.01145 (2021).

  49. Kennes, D. M. et al. Moiré heterostructures as a condensed-matter quantum simulator. Nat. Phys. 17, 155–163 (2021).

    Google Scholar 

  50. Chen, G. et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene moiré superlattice. Nat. Phys. 15, 237–241 (2019).

    Google Scholar 

  51. Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).

    ADS  Google Scholar 

Download references

Acknowledgements

We thank D. Goldhaber-Gordon and O. Vafek for helpful discussions. This work was supported by the QSQM, an Energy Frontier Research Center funded by the US Department of Energy (DOE), Office of Science, Basic Energy Sciences (BES), under award no. DE-SC0021238. B.E.F. acknowledges a Stanford University Terman Fellowship and an Alfred P. Sloan Foundation Fellowship. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by MEXT, Japan (grant no. JPMXP0112101001) and JSPS KAKENHI (grant no. JP20H00354). S.A.K. acknowledges support from the Department of Energy, Office of Basic Energy Sciences, under contract no. DEAC02-76SF00515. B.A.F. acknowledges a Stanford Graduate Fellowship. M.E.B. acknowledges support from the Marvin Chodorow Postdoctoral Fellowship of the Applied Physics Department, Stanford University. Y.S. was supported by the Gordon and Betty Moore Foundation’s EPiQS Initiative through grants GBMF 4302 and GBMF 8686. P.P. acknowledges partial support from NSF grant DMR-2111379. Part of this work was performed at the Stanford Nano Shared Facilities (SNSF), supported by the National Science Foundation under award ECCS-2026822.

Author information

Authors and Affiliations

  1. Department of Applied Physics, Stanford University, Stanford, CA, USA

    Jiachen Yu, Mark E. Barber & Zhi-Xun Shen

  2. Geballe Laboratory of Advanced Materials, Stanford University, Stanford, CA, USA

    Jiachen Yu, Benjamin A. Foutty, Mark E. Barber, Zhi-Xun Shen, Steven A. Kivelson & Benjamin E. Feldman

  3. Department of Physics, Stanford University, Stanford, CA, USA

    Benjamin A. Foutty, Zhaoyu Han, Yoni Schattner, Zhi-Xun Shen, Steven A. Kivelson & Benjamin E. Feldman

  4. Stanford Institute for Materials and Energy Sciences, SLAC National Accelerator Laboratory, Menlo Park, CA, USA

    Yoni Schattner, Zhi-Xun Shen & Benjamin E. Feldman

  5. Research Center for Functional Materials, National Institute for Material Science, Tsukuba, Japan

    Kenji Watanabe

  6. International Center for Materials Nanoarchitectonics, National Institute for Material Science, Tsukuba, Japan

    Takashi Taniguchi

  7. Department of Physics and Institute for Condensed Matter Theory, University of Illinois at Urbana-Champaign, Urbana, IL, USA

    Philip Phillips

Authors
  1. Jiachen Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Benjamin A. Foutty
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhaoyu Han
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mark E. Barber
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yoni Schattner
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Kenji Watanabe
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Takashi Taniguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Philip Phillips
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Zhi-Xun Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Steven A. Kivelson
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. Benjamin E. Feldman
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

J.Y., B.A.F. and B.E.F. designed and conducted the scanning SET experiments. M.E.B. and Z.-X.S. designed and conducted the MIM experiments. B.A.F. fabricated the sample. Z.H., Y.S., S.A.K. and P.P. contributed to theoretical analysis. K.W. and T.T. provided hBN crystals. All authors participated in discussions and in writing of the manuscript.

Corresponding author

Correspondence to Benjamin E. Feldman.

Ethics declarations

Competing interests

Z.-X.S. is a co-founder of PrimeNano Inc., which licensed the MIM technology from Stanford University for commercial instruments.

Peer review

Peer review information

Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 Spatial dependence of electronic compressibility at zero field.

Linecut of dμ/dn as a function of gate voltage (Vg) measured along a line in the top left contact area of the device shown in Fig. 1a. The Landau fans shown in Fig. 1 and Extended Data Fig. 4 are taken at x = 40 nm and x = 300 nm, respectively. The sawtooth pattern on the electron side generically exhibits a larger amplitude and negative dμ/dn at the ν = 2 transition. Dashed lines denote gate voltages corresponding to ν = ±4.

Extended Data Fig. 2 Spatial dependence of zLL and ChIs.

Linecut of dμ/dn at 11 T. The positions with x > 0 correspond to those shown in Extended Data Fig. 1. While the overall strengths of the broken-symmetry zLLs is spatially dependent, those at odd integers have comparable strengths to those at even integers independent of position.

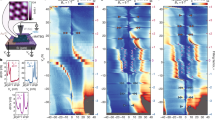
Extended Data Fig. 3 Comparison of inverse electronic compressibility and MIM measurements.

Selected dμ/dn measurements as a function of moiré filling factor ν at different perpendicular magnetic fields reproduced from Fig. 1d. The curves are vertically spaced according to the applied magnetic field and the grey lines indicate the field dependence of the incompressible states identified in Fig. 1e. b, MIM measurements of the local conductivity at the same sample position as a function of ν and at the same magnetic fields. A decrease in MIM-Im corresponds to a decrease in conductivity confirming the main ChI and zLLs are associated with local resistive behavior. The MIM measurements were taken at T = 450 mK.

Source data

Extended Data Fig. 4 Landau fan of ChIs at a second location.

dμ/dn measured at a second location (blue dot in Fig. 1a) with twist angle θ = 1.09˚ showing qualitatively similar ChIs/zLLs sequences and phase boundaries as in Fig. 1d.

Extended Data Fig. 5 Landau fan at higher temperature.

dμ/dn measured at the location of Fig. 1d at temperature T = 1.7 K. The ChIs/zLLs and negative dμ/dn features are thermally broadened and weakened, but the qualitative pattern is unchanged. Interestingly, negative dμ/dn features that mark phase transitions appear closer to the adjacent incompressible states.

Extended Data Fig. 6 Spatial dependence and competing ChIs.

Higher resolution Landau fans in the vicinity of (𝜈 = −8/3, B = 8.7 T) taken in the locations of Fig. 1d and Extended Data Fig. 4. The pattern of dominant ChIs and detailed regions of negative dμ/dn are distinct in each location. c-e, Spatial linecuts (same trajectory as in Extended Data Fig. 1) taken at B = 9.4, 8.7, and 7.4 T, respectively.

Extended Data Fig. 7 Hofstadter spectrum from a second location.

Correlated Hofstadter spectrum extracted from the data in Extended Data Fig. 4. The spectrum qualitatively agrees with that in Fig. 2c with a slightly smaller total bandwidth.

Extended Data Fig. 8 Hysteresis as a function of B.

dμ/dn measured as a function of both increasing (red) and decreasing (blue) B at fixed densities. Hysteretic regions are highlighted in yellow. d-e, Hysteresis as a function of density, reproduced from Fig. 3a, d. Overlaid yellow lines indicate ranges over which we observe hysteresis as a function of B. Solid (dashed) lines indicate dμ/dnup − dμ/dndown > 0 (<0), respectively. The ranges of ν and B in which hysteresis occurs are independent of which is swept as the fast axis.

Source data

Extended Data Fig. 9 zLL gap evolution at a second location.

Thermodynamic gaps of νC = ±2 zLLs extracted from the data presented in Extended Data Fig. 4.

Source data

Extended Data Fig. 10 Phenomenological model of zLL evolution in the presence of mirror symmetry breaking.

Schematic of the moiré valley splitting Δv between \(\kappa _M,\kappa _M^\prime\) by Δv. b, Evolution of the zLLs in the presence of inter-flavor Coulomb repulsion U (ignoring single-particle effects). Four zLLs with different flavors are split linearly in B within each moiré valley (red and blue, respectively), resulting in LL crossings. The corresponding Chern numbers are labeled within the gaps. c, B dependence of zLL gaps derived from b. d, Evolution of the zLLs if the Zeeman coupling is different for spin and valley flavors. Such single-particle gaps lead to different effective interactions U and U’ between LLs corresponding to different flavors within each moiré valley. This modifies the fields at which LL crossings occur, reducing B1, B2 and B3 relative to the predicted field \(B_1^\prime\) at which the gaps at |νC| = 2 close and those at odd integer fillings saturate. e, B dependence of the zLL gaps derived from d.

Supplementary information

Supplementary information

Supplementary Sections 1–9, Figs. 1–4, Tables 1 and 2, and References.

Source data

Source Data Fig. 1

Data for all line plots.

Source Data Fig. 3

Data for all line plots.

Source Data Fig. 4

Data for all line plots.

Source Data Extended Data Fig. 3

Data for all line plots.

Source Data Extended Data Fig. 8

Data for all line plots.

Source Data Extended Data Fig. 9

Data for all line plots.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, J., Foutty, B.A., Han, Z. et al. Correlated Hofstadter spectrum and flavour phase diagram in magic-angle twisted bilayer graphene. Nat. Phys. 18, 825–831 (2022). https://doi.org/10.1038/s41567-022-01589-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-022-01589-w

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing