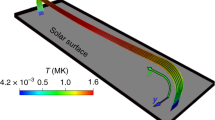
Abstract
Spicules are plasma jets that are observed in the dynamic interface region between the visible solar surface and the hot corona. At any given time, it is estimated that about 3 million spicules are present on the Sun. We find an intriguing parallel between the simulated spicular forest in a solar-like atmosphere and the numerous jets of polymeric fluids when both are subjected to harmonic forcing. In a radiative magnetohydrodynamic numerical simulation with sub-surface convection, solar global surface oscillations are excited similarly to those harmonic vibrations. The jets thus produced match remarkably well with the forests of spicules detected in observations of the Sun. Taken together, the numerical simulations of the Sun and the laboratory fluid dynamics experiments provide insights into the mechanism underlying the ubiquity of jets. The non-linear focusing of quasi-periodic waves in anisotropic media of magnetized plasma as well as polymeric fluids under gravity is sufficient to generate a forest of jets.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Data availability
Source data for Fig. 1a,b,e,f and Extended Data Fig. 6 are provided with this paper. The data for Fig. 2a and Extended Fig. 3a,b can be downloaded from iris.lmsal.com. The raw simulation data files in Fortran binary format (about 300 GB in size) used to produce Fig. 2b,c are available from the corresponding author upon reasonable request.
Code availability
The Pencil code is hosted at https://github.com/pencil-code/. The run directory for simulation with solar convection represented in Fig. 2b is publicly available at https://doi.org/10.5281/zenodo.5807020 upon request.
References
Beckers, J. M. Solar spicules. Ann. Rev. Astron. Astrophys. 10, 73–100 (1972).
Sterling, A. C. Solar spicules: a review of recent models and targets for future observations (invited review). Sol. Phys. 196, 79–111 (2000).
Tsiropoula, G. et al. Solar fine-scale structures. I. spicules and other small-scale, jet-like events at the chromospheric level: observations and physical parameters. Space Sci. Rev. 169, 181–244 (2012).
Roberts, B. Spicules: the resonant response to granular buffeting? Sol. Phys. 61, 23–34 (1979).
Hollweg, J. V. On the origin of solar spicules. Astrophys. J. 257, 345–353 (1982).
Suematsu, Y., Shibata, K., Nishikawa, T. & Kitai, R. Numerical hydrodynamics of the jet phenomena in the solar atmosphere - Part one - Spicules. Sol. Phys. 75, 99–118 (1982).
Iijima, H. & Yokoyama, T. Effect of coronal temperature on the scale of solar chromospheric jets. Astrophys. J. 812, L30 (2015).
De Pontieu, B., Erdélyi, R. & James, S. P. Solar chromospheric spicules from the leakage of photospheric oscillations and flows. Nature 430, 536–539 (2004).
Heggland, L., Pontieu, B. D. & Hansteen, V. H. Numerical simulations of shock wave–driven chromospheric jets. Astrophys. J. 666, 1277–1283 (2007).
Heggland, L., Hansteen, V. H., De Pontieu, B. & Carlsson, M. Wave propagation and jet formation in the chromosphere. Astrophys. J. 743, 142 (2011).
Haerendel, G. Weakly damped Alfvén waves as drivers of solar chromospheric spicules. Nature 360, 241–243 (1992).
Liu, J., Nelson, C. J., Snow, B., Wang, Y. & Erdélyi, R. Evidence of ubiquitous Alfvén pulses transporting energy from the photosphere to the upper chromosphere. Nat. Comm. 10, 3504 (2019).
Sterling, A. C., Mariska, J. T., Shibata, K. & Suematsu, Y. Numerical simulations of microflare evolution in the solar transition region and corona. Astrophys. J. 381, 630–633 (1991).
Shibata, K. et al. Chromospheric anemone jets as evidence of ubiquitous reconnection. Science 318, 1591–1594 (2007).
Samanta, T. et al. Generation of solar spicules and subsequent atmospheric heating. Science 366, 890–894 (2019).
Martínez-Sykora, J. et al. On the generation of solar spicules and Alfvénic waves. Science 356, 1269–1272 (2017).
Iijima, H. & Yokoyama, T. A three-dimensional magnetohydrodynamic simulation of the formation of solar chromospheric jets with twisted magnetic field lines. Astrophys. J. 848, 38 (2017).
Faraday, M. On the forms and states of fluids on vibrating elastic surfaces. Philos. Trans. Soc. Lond. 52, 319–340 (1831).
Rajchenbach, J., Clamond, D. & Leroux, A. Observation of star-shaped surface gravity waves. Phys. Rev. Lett. 110, 094502 (2013).
Goodridge, C. L., Hentschel, H. G. E. & Lathrop, D. P. Threshold dynamics of singular gravity–capillary waves. Phys. Rev. Lett. 76, 1824–1827 (1996).
Wagner, C., Müller, H. W. & Knorr, K. Faraday waves on a viscoelastic liquid. Phys. Rev. Lett. 83, 308–311 (1999).
Cabeza, C. & Rosen, M. Complexity in faraday experiment with viscoelastic fluid. Int. J. Bifurc. Chaos 17, 1599–1607 (2007).
Longcope, D. W., McLeish, T. C. B. & Fisher, G. H. A viscoelastic theory of turbulent fluid permeated with fibril magnetic fields. Astrophys. J. 599, 661–674 (2003).
Ogilvie, G. I. & Proctor, M. R. E. On the relation between viscoelastic and magnetohydrodynamic flows and their instabilities. J. Fluid Mech. 476, 389–409 (2003).
García, R. A. et al. Global solar Doppler velocity determination with the GOLF/SoHO instrument. Astron. Astrophys. 442, 385–395 (2005).
Uchida, Y. On the formation of solar chromospheric spicules and flare surges. Pub. Astron. Soc. Jpn. 13, 321–334 (1961).
Goodridge, C. L., Shi, W. T., Hentschel, H. G. E. & Lathrop, D. P. Viscous effects in droplet-ejecting capillary waves. Phys. Rev. E 56, 472–475 (1997).
Dinic, J. & Sharma, V. Macromolecular relaxation, strain, and extensibility determine elastocapillary thinning and extensional viscosity of polymer solutions. Proc. Natl Acad. Sci. USA 116, 8766–8774 (2019).
Plateau, J. A. F. Statique Experimentale et Theorique des Liquides Soumis aux Seules Forces Moleculaires, vol. 2 (Trübner, 1873).
Rayleigh, L. On the instability of a cylinder of viscous liquid under capillary force. Philos. Mag. 34, 145–154 (1892).
Zeff, B. W., Kleber, B., Fineberg, J. & Lathrop, D. P. Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 403, 401–404 (2000).
Lemen, J. R. et al. The Atmospheric Imaging Assembly (AIA) on the Solar Dynamics Observatory (SDO). Sol. Phys. 275, 17–40 (2012).
De Pontieu, B. et al. The Interface Region Imaging Spectrograph (IRIS). Sol. Phys. 289, 2733–2779 (2014).
Pereira, T. M. D. et al. An interface region imaging spectrograph first view on solar spicules. Astrophys. J. Lett. 792, L15 (2014).
Anan, T. et al. Spicule dynamics over a plage region. Pub. Astron. Soc. Jpn. 62, 871–877 (2010).
De Pontieu, B. et al. A tale of two spicules: the impact of spicules on the magnetic chromosphere. Pub. Astron. Soc. Jpn. 59, S655–S662 (2007).
Hansteen, V. H., De Pontieu, B., Rouppe van der Voort, L., van Noort, M. & Carlsson, M. Dynamic fibrils are driven by magnetoacoustic shocks. Astrophys. J. Lett. 647, L73–L76 (2006).
Henriques, V. M. J., Kuridze, D., Mathioudakis, M. & Keenan, F. P. Quiet-Sun Hα transients and corresponding small-scale transition region and coronal heating. Astrophys. J. 820, 124 (2016).
Martínez-Sykora, J., Hansteen, V., Pontieu, B. D. & Carlsson, M. Spicule-like structures observed in three-dimensional realistic magnetohydrodynamic simulations. Astrophys. J. 701, 1569–1581 (2009).
Sakaue, T. & Shibata, K. Energy transfer by nonlinear Alfvén waves in the solar chromosphere and its effect on spicule dynamics, coronal heating, and solar wind acceleration. Astrophys. J. 900, 120 (2020).
Heinemann, T., Dobler, W., Nordlund, Å & Brandenburg, A. Radiative transfer in decomposed domains. Astron. Astrophys. 448, 731–737 (2006)..
Chatterjee, P. Testing Alfvén wave propagation in a “realistic” set-up of the solar atmosphere. Geophys. Astrophys. Fluid Dyn. 114, 213–234 (2020).
Cook, J. W., Cheng, C. C., Jacobs, V. L. & Antiochos, S. K. Effect of coronal elemental abundances on the radiative loss function. Astrophys. J. 338, 1176–1183 (1989).
Christensen-Dalsgaard, J. et al. The current state of solar modeling. Science 272, 1286–1292 (1996).
Vernazza, J. E., Avrett, E. H. & Loeser, R. Structure of the solar chromosphere. III. Models of the EUV brightness components of the quiet Sun. Astrophys. J. Suppl. Ser. 45, 635–725 (1981).
Kriginsky, M. et al. Ubiquitous hundred-Gauss magnetic fields in solar spicules. Astron. Astrophys. 642, A61 (2020).
Keil, S. L. & Canfield, R. C. The height variation of velocity and temperature fluctuations in the solar photosphere. Astron. Astrophys. 70, 169–179 (1978).
Brandenburg, A. & Dobler, W. Hydromagnetic turbulence in computer simulations. Comput. Phys. Commun. 147, 471–475 (2002).
Brandenburg, A. et al. The Pencil code, a modular MPI code for partial differential equations and particles: multipurpose and multiuser-maintained. J. Open Source Softw. 6, 2807 (2021).
Haugen, N. E. L., Brandenburg, A. & Mee, A. J. Mach number dependence of the onset of dynamo action. Monthly Not. R. Astron. Soc. 353, 947–952 (2004).
Chatterjee, P. & Dey, S. Configuration files for simulations of the solar spicule forest. Zenodo https://doi.org/10.5281/zenodo.5807020 (2022).
Lumley, J. L. & Newman, G. R. The return to isotropy of homogeneous turbulence. J. Fluid Mech. 82, 161–178 (1977).
Landi, E. & Chiuderi Drago, F. The quiet-Sun differential emission measure from radio and UV measurements. Astrophys. J. 675, 1629–1636 (2008).
Rempel, M. Extension of the MURAM radiative MHD code for coronal simulations. Astrophys. J. 834, 10 (2016).
Van Doorsselaere, T., Antolin, P., Yuan, D., Reznikova, V. & Magyar, N. Forward modelling of optically thin coronal plasma with the FoMo tool. Front. Astron. Space Sci. 3, 4 (2016).
Dere, K. P., Landi, E., Mason, H. E., Monsignori Fossi, B. C. & Young, P. R. CHIANTI – an atomic database for emission lines. Astron. Astrophys. Suppl. 125, 149–173 (1997).
Goodridge, C. L., Hentschel, H. G. E. & Lathrop, D. P. Breaking Faraday waves: critical slowing of droplet ejection rates. Phys. Rev. Lett. 82, 3062–3065 (1999).
Boldyrev, S., Huynh, D. & Pariev, V. Analog of astrophysical magnetorotational instability in a Couette–Taylor flow of polymer fluids. Phys. Rev. E 80, 066310 (2009).
Bai, Y., Crumeyrolle, O. & Mutabazi, I. Viscoelastic Taylor–Couette instability as analog of the magnetorotational instability. Phys. Rev. E 92, 031001 (2015).
Skogsrud, H., Rouppe van der Voort, L., De Pontieu, B. & Pereira, T. M. D. On the temporal evolution of spicules observed with IRIS, SDO, and Hinode. Astrophys. J. 806, 170 (2015).
Acknowledgements
Computing time provided by Nova HPC at IIA as well as Param Yukti facility at JNCASR under National Supercomputing Mission, Govt. of India is gratefully acknowledged. This work has also utilized SahasraT facility at SERC, IISc for computing and CENSe, IISc for rheometry. S.D. and P.C. thank IIA for financial support towards the usage of SahasraT. S.D. also acknowledges the SOLARNET project that has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement no. 824135. M.O.V.S.N. acknowledges a grant RC00226 to study Faraday oscillations in fluids from the Azim Premji University. M.B.K. thanks the Science and Technology Facilities Council (STFC) for the ST/S000518/1 grant. J.L. acknowledges the support from the Leverhulme Trust via grant RPG-2019-371. C.J.N. thanks STFC for the support received to conduct this research through grant nos. ST/P000304/1 and ST/T00021X/1. R.E. is grateful to STFC (grant no. ST/M000826/1), the Royal Society and the President’s International Fellowship Initiative of the Chinese Academy of Sciences (grant no. 2019VMA052) for enabling this research. R.E. also acknowledges the support received from the Higher Education Programme of Excellence for Particle and Astrophysics, Eötvös L. University (Budapest, Hungary). We thank C. Kalelkar for several discussions on polymeric fluids. IRIS is a NASA small explorer mission developed and operated by LMSAL with major contributions to downlink communications funded by ESA and the Norwegian Space Centre. The accelerated solar global p mode observations used to construct Supplementary Video 5 were obtained by the SoHO/MDI instrument. We used the visualisation software Paraview for volume rendering for Supplementary Video 3.
Author information
Authors and Affiliations
Contributions
P.C. and M.O.V.S.N. conceptualized the study. P.C. prepared the numerical simulation set-up of the solar atmosphere. P.C. and S.D. performed the simulations, analysed the results and prepared the figures and animations with contributions from J.L. on ASDA and spicule statistics and suggestions from R.E. The fluid experiments were designed and conducted by M.O.V.S.N. The experimental data were analysed by M.O.V.S.N. with contributions from P.C., S.D. and M.B.K. The IRIS data analysis was performed by M.B.K. and R.E., who also prepared the corresponding figures with contributions from C.J.N. and J.L. The p mode time series was provided by R.E. The manuscript was drafted by P.C. and M.O.V.S.N. with input from R.E. All authors contributed to the interpretation of the results and worked on the subsequent versions of the manuscript together.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial or non-financial interests.
Peer review
Peer review information
Nature Physics thanks the anonymous reviewers for their contribution to the peer review of this work
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Signature of polymer stretching.
(a) The set up for the polarization experiment for detecting polymeric stretching in 2% Poly Vinyl Alcohol. He-Ne laser light passes through a polarizer and then through the sample region of interest probing the jets, to be collected after an analyzer by an imaging device. By varying the angle of the polarizer-analyzer combination at right angles to each other, the polarization state of the jets can be determined (see Methods). (b) Jets of iodinated 2% aqueous PVA by Faraday excitation at 30 Hz. (c) Similar to (b) but seen through the polarizer set-up in (a) to highlight stretching of polymer threads.
Extended Data Fig. 2 Kelvin-Helmholtz instability and magnetic field.
(a) Contours of temperature in the simulation domain with zero imposed magnetic field shows turbulence generated by the Kelvin-Helmholtz instability. (b) Same as (a) with the addition of a damping term in the horizontal velocity equation to mimic suppression of turbulence in the horizontal direction.
Extended Data Fig. 3 Observed and simulated spicules seen in Si IV and Mg II emission lines.
(a) Spicules seen at the solar limb with the Si IV filter of IRIS. (b) Same as (a) but for IRIS Mg II k filter. (c) Shaded contours of synthetic intensity of Si IV emission synthesized using the CHIANTI package available in the FoMo code, for the simulation run with imposed vertical magnetic field Bimp = 74 G at time, t = 152.50 min from the start are shown in the [x, z]-plane. (d) Same as (c) but for emission at Mg II k also using CHIANTI. The cyan rectangle in panels (a) and (b) indicates the same extent as the simulation domain shown in (c)-(d).
Extended Data Fig. 4 Propagation of shock compression and hyper-sonic regions.
(a) Time-distance map of the Mach number, Ma (blue shaded), and shock compression (red contour lines) for a vertical slit at x = 2.5Mm of panel (a). The regions of plasma compression, ∇ ⋅ V < 0, are found to coincide with acceleration fronts, shown in Fig. 3c, where the spicular plasma is energised to hypersonic speeds. The characteristic curve for acoustic waves is denoted by the solid black line.
Extended Data Fig. 5 Plasma heating processes.
(a) Synthetic Si IV emission from the simulated spicule forest similar to Fig. 3c calculated using CHIANTI. The green contours denote the locations of plasma heating above 103Ks−1 only due to the local compression of plasma, − (γ − 1)T ∇ ⋅ V, where T and V are the plasma temperature and velocity, respectively. The ratio of specific heats denoted, γ = cP/cV, has been calculated using the equation of state for a partially ionized ideal gas. (b) Regions of Mach number, Ma > 1, are indicated by shaded blue contours. Here, the green contours show heating above 103Ks−1 only due to dissipation inside the shocks by ζshock(∇⋅V)2/cV, where ζshock is the shock viscosity. (c) Strength of various heating sources as function of height in the atmosphere. Horizontally averaged heating profiles, 〈H〉(z) due to local plasma compression (red-dashed), shock dissipation (black-solid), and Ohmic heating (blue dot-dashed).
Extended Data Fig. 6 Comparing height distribution of solar spicules and fluid jets.
(a) Histogram for distribution of \(H=(h-{h}_{\min })/({h}_{\max }-{h}_{\min })\), where h is the maximum height reached by a spicule and \({h}_{\min }\), \({h}_{\max }\) are the minimum and maximum heights of a sample of unique spicules (sample size 216 and counted during 40min of solar time), respectively, as seen in synthetic emission at T = 15, 000 K from the simulation shown in Extended Fig. 3b. (b) The distribution of H from a sample of unique fluid jets (sample size 224 and counted during 10 excitation periods post the central jet ejection) in an experiment with iodinated 2% PVA. Note that only spicules such that 6 < h < 24.9 Mm and fluid jets such that 0.5 < h < 4.5cm have been included in the distribution. The lower limit in the simulation is chosen because individual spicules cannot be discerned if they are below 6Mm, whereas, in the experiment the lower end is set by the container height of 0.5cm. The upper limits are the maximum heights obtained in the experiments. (c) The cumulative distribution function (CDF) to indicate the number of jets above \(h > {h}_{\min }\) for both plasma and polymeric fluid.
Extended Data Fig. 7 Phase plot of vertical component of velocity, vz versus acceleration, az.
(a) The region around a shorter spicule above an inter granular lane squeezing site used for the calculation at t = 15.33min from the start of tracking. Each dot denotes a Lagrangian particle colored by its instantaneous vertical velocity, vz. The yellow contours are magnetic field lines. (b) vz versus az. (c) vz versus the vertical acceleration only due to the Lorentz force. Note that the particles considered, initially at t = 0 lie in layers 0 < z < 3Mm. Every dots denotes a particle and colored by its instantaneous vertical position. (d) The region where a longer spicule takes birth just above a granule at t = 17.50min. The magnetic field lines are shown by black contours. (e) and (f) are same as (b) and (c), respectively, but, for the case of the longer spicule shown in (d).
Extended Data Fig. 8 Solar atmospheric stratification with convection.
(a) Temperature structure at the time of introduction of Lagrangian particles in the domain for the same run shown in Fig. 3a. The white solid line is the optical depth, τ = 0.1 surface. (b) The density at the same instant as (a). The plasma β = 1 surface is denoted by the black solid line. (c) The vertical velocity, vz corresponding to panels (a) and (b).
Supplementary information
Supplementary Video 1
Response of solar plasma to superposition of frequencies: (a) Synthetic Si-IV emission according to the analytical expression given by Eq.2 from a model driven by a velocity forcing of the form \({v}_{z}/{V}_{0}=\sin (2\pi {f}_{1}t)/4+\sin (2\pi {f}_{2}t)/2+\sin (2\pi {f}_{3}t)/4\) shown in panel (c), where V0 = 1.0kms−1, f1 = 3.0 mHz, f2 = 3.5 mHz, and f3 = 4.0 mHz. The above forcing has only been applied within a layer, − 50 km < z < 0 km. (b) Same as (a) but for temperature (in Kelvin).
Supplementary Video 2
Jet breaking in polymeric fluid (PEO, 1000 ppm, viscoelastic) versus 55% glycerine solution (viscous) at two different frequencies (a) 120 Hz, and (b) 30 Hz with acceleration amplitudes in terms of local gravity indicated. (c) Polymeric fluids (iodinated 2% PVA, 23% jets reaching heights above 1 cm break) may resist droplet ejection by pinching of jets (due to Plateau-Rayleigh instability) as compared to Newtonian fluids (76% Glycerine solution, 53% jet-breakage above 1 cm) of similar viscosity and surface tension. Both fluids are subjected to similar peak forcing of 10.1gE (30 ml fluid in cylindrical container).
Supplementary Video 3
Nonlinear development in numerical and table-top experiment: volume rendering of synthetic emission at 15000 K for a three-dimensional numerical simulation of solar plasma forced at the lower boundary with a periodic forcing with a velocity amplitude of 1.32 km s−1 and an imposed magnetic field of 10 G (left panel). A polymeric fluid (iodinated 3% PVA solution) subjected to Faraday excitation at 30 Hz and a peak acceleration of 10.1gE (right panel). Both the numerical and the table-top experiments show nonlinear development in about five oscillation periods.
Supplementary Video 4
Mechanism of formation of fluid jets: View of the free surface of iodinated 3% PVA, as seen at an angle of 20∘ from the vertical, to show the mechanism for jet forest formation by collision of ridges of neighbouring polygonal cells formed due to interacting surface gravity waves (via nonlinear mode coupling).
Supplementary Video 5
Response of polymeric fluid to frequency scaled solar p-modes: Iodinated 2% PVA (30 ml) placed in a circular container of 0.1 m diameter and responding to frequency-scaled quasi-periodic solar acoustic modes (p-modes from SOHO/MDI) such that the dominant FFT peak lies at 30 Hz. The peak acceleration reaches up to 5gE. Imaged at 500 fps.
Supplementary Video 6
Synthetic emission at a temperature of 80000 K calculated using the analytical expression of Eq. (2) (top panel) and AIA 17.1 nm emission from our numerical simulation (bottom panel). Magnetic fields are shown by red curves.
Supplementary Video 7
Faraday excitation experiment with paint: Initially separate red (15 ml) and white (15 ml) paint in a circular container of diameter 0.1 m responding to a 30 Hz harmonic Faraday excitation with a peak acceleration of 7gE imaged at 1000 fps. We observe the abundant formation of jet forest, some of which exhibit rotation as visualized by twisted motion of the red and white threads of paint.
Supplementary Video 8
Lagrangian tracking of the plasma in the spicule forest: (a) 540000 particles are initially distributed uniformly in six differently coloured layers, each with 1 Mm thickness except the bottom one which is 0.5 Mm thick, between − 0.5 < z < 5 Mm. (b) and (c) Particles are tracked by local acceleration and vertical velocity to show acceleration fronts energizing the spicular plasma. Black curves in (b) show magnetic field lines whereas the black contours in (c) denote regions of shock. (d) Spicule formation driven by granular collapse in convective plumes, P1 and P2. (e) Spicule formation driven by solar global oscillations and magnetic reconnection (denoted by the white rectangle).
Supplementary Video 9
Determination of \({A}_{\min }\) in A0 versus f0 phase space: Part I (solar atmosphere): Spicules formed in response to wave driving of the form \(2\pi {f}_{0}{V}_{0}\sin (2\pi {f}_{0}t)\cos (5\pi x/L)\), with (a) V0 = 0.5 kms−1, (b) V0 = 0.35 and (c) 0.25 kms−1, respectively. The dashed line indicates the 7 Mm height. Note that the forest of jet criteria is satisfied for cases (a) and (b) only. Part II (Polymeric fluid): Jets formed in response to Faraday excitation with peak accelerations, A0 as (a) 4.1gE, (b) 3.6gE, (c) 4.3gE, and (d) 4.7gE. The dotted line denotes the 1.3 cm mark on the scale. Only (c) and (d) satisfy the forest of jets criteria.
Source data
Source Data Fig. 1
Contains: Data points f0 vs A0 in csv format for threshold acceleration in solar atmosphere necessary for spicule formation (Fig. 1a). Data points f0 vs A0 in csv format for threshold acceleration in PEO necessary for jet formation (Fig. 1b) Anisotropy varying with magnetic field in solar atmospheric simulation (Fig. 1e). Anisotropy varying with polymer concentration in experiment with PEO (Fig. 1f).
Source Data Extended Data Fig. 6
Height values for 216 spicules from two different data sets. Set 1 for 136 unique spicules and set 2 for 80 unique spicules sampled from two different simulation runs with convection (Extended Data Fig 6a). Also includes height values for 224 unique jets from iodinated 2% Poly Vinyl Alcohol solution subjected to harmonic vibration at 30 Hz (Extended Data Fig. 6b).
Rights and permissions
About this article
Cite this article
Dey, S., Chatterjee, P., O. V. S. N., M. et al. Polymeric jets throw light on the origin and nature of the forest of solar spicules. Nat. Phys. 18, 595–600 (2022). https://doi.org/10.1038/s41567-022-01522-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-022-01522-1
This article is cited by
-
Fluid jets on bass speaker solve mystery of Sun’s ‘burning prairie’
Nature India (2022)