Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Rotation symmetry breaking in the normal state of a kagome superconductor KV3Sb5

Nature Physics volume 18, pages 265–270 (2022)Cite this article

Subjects

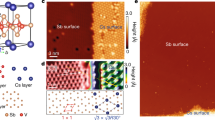
Abstract

Recently discovered superconductors AV3Sb5 (A = K, Rb, Cs)1,2 provide a fresh opportunity to study correlation-driven electronic phenomena on a kagome lattice. The observation of an unusual charge density wave (CDW) in the normal state of all the members of the AV3Sb5 family2,3,4,5,6,7,8,9,10 has prompted a large effort to identify any ‘hidden’ broken symmetries associated with it. We use spectroscopic-imaging scanning tunnelling microscopy to reveal pronounced intensity anisotropy between the different directions of hexagonal CDW in KV3Sb5. In particular, we find that one of the CDW directions is distinctly different compared with the other two. This observation points to an intrinsic rotation-symmetry-broken electronic ground state where the symmetry is reduced from sixfold to twofold. Furthermore, in contrast to previous reports3, we find that the CDW phase is insensitive to the magnetic-field direction, regardless of the presence or absence of atomic defects. Our experiments, combined with earlier observations of stripe charge ordering in CsV3Sb5, establish correlation-driven rotation symmetry breaking as a unifying feature of AV3Sb5 kagome superconductors.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Crystal structure of KV3Sb5 and surface morphology.
Fig. 2: Spectroscopic-imaging scanning tunnelling microscopy of the Sb surface.
Fig. 3: Anisotropy between inequivalent CDW directions and its atomic-scale signature in spectroscopic maps.
Fig. 4: Insensitivity of CDW to external magnetic-field direction.

Data availability

Source data are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.

Code availability

The computer code used for data analysis is available from the corresponding author upon reasonable request.

References

  1. Ortiz, B. R. et al. New kagome prototype materials: discovery of KV3Sb5, RbV3Sb5, and CsV3Sb5. Phys. Rev. Mater. 3, 094407 (2019).

    Article  Google Scholar 

  2. Ortiz, B. R. et al. CsV3Sb5: a Z2 topological kagome metal with a superconducting ground state. Phys. Rev. Lett. 125, 247002 (2020).

    Article  ADS  Google Scholar 

  3. Jiang, Y.-X. et al. Unconventional chiral charge order in kagome superconductor KV3Sb5. Nat. Mater. 20, 1353–1357 (2021).

    Google Scholar 

  4. Zhao, H. et al. Cascade of correlated electron states in the kagome superconductor CsV3Sb5. Nature 599, 216–221 (2021).

    Article  ADS  Google Scholar 

  5. Liang, Z. et al. Three-dimensional charge density wave and surface-dependent vortex-core states in a kagome superconductor CsV3Sb5. Phys. Rev. X 11, 031026 (2021).

    Google Scholar 

  6. Chen, H. et al. Roton pair density wave in a strong-coupling kagome superconductor. Nature 599, 222–228 (2021).

    Article  ADS  Google Scholar 

  7. Yu, F. H. et al. Concurrence of anomalous Hall effect and charge density wave in a superconducting topological kagome metal. Phys. Rev. B 104, L041103 (2021).

    Article  ADS  Google Scholar 

  8. Li, H. et al. Observation of unconventional charge density wave without acoustic phonon anomaly in kagome superconductors AV3Sb5 (A = Rb, Cs). Phys. Rev. X 11, 031050 (2021).

    Google Scholar 

  9. Chen, K. Y. et al. Double superconducting dome and triple enhancement of Tc in the kagome superconductor CsV3Sb5 under high pressure. Phys. Rev. Lett. 126, 247001 (2021).

    Article  ADS  Google Scholar 

  10. Wang, Z. et al. Distinctive momentum dependent charge-density-wave gap observed in CsV3Sb5 superconductor with topological kagome lattice. Preprint at https://arxiv.org/abs/2104.05556 (2021).

  11. Sachdev, S. Kagome- and triangular-lattice Heisenberg antiferromagnets: ordering from quantum fluctuations and quantum-disordered ground states with unconfined bosonic spinons. Phys. Rev. B 45, 12377–12396 (1992).

    Article  ADS  Google Scholar 

  12. Guo, H.-M. & Franz, M. Topological insulator on the kagome lattice. Phys. Rev. B 80, 113102 (2009).

    Article  ADS  Google Scholar 

  13. Neupert, T., Santos, L., Chamon, C. & Mudry, C. Fractional quantum Hall states at zero magnetic field. Phys. Rev. Lett. 106, 236804 (2011).

    Article  ADS  Google Scholar 

  14. Sun, K., Gu, Z., Katsura, H. & Das Sarma, S. Nearly flatbands with nontrivial topology. Phys. Rev. Lett. 106, 236803 (2011).

    Article  ADS  Google Scholar 

  15. Tang, E., Mei, J.-W. & Wen, X.-G. High-temperature fractional quantum Hall states. Phys. Rev. Lett. 106, 236802 (2011).

    Article  ADS  Google Scholar 

  16. Wang, Q. et al. Large intrinsic anomalous Hall effect in half-metallic ferromagnet Co3Sn2S2 with magnetic Weyl fermions. Nat. Commun. 9, 3681 (2018).

    Article  ADS  Google Scholar 

  17. Morali, N. et al. Fermi-arc diversity on surface terminations of the magnetic Weyl semimetal Co3Sn2S2. Science 365, 1286–1291 (2019).

    Article  ADS  Google Scholar 

  18. Liu, E. et al. Giant anomalous Hall effect in a ferromagnetic kagome-lattice semimetal. Nat. Phys. 14, 1125–1131 (2018).

    Article  Google Scholar 

  19. Yin, J.-X. X. et al. Giant and anisotropic many-body spin–orbit tunability in a strongly correlated kagome magnet. Nature 562, 91–95 (2018).

    Article  ADS  Google Scholar 

  20. Kang, M. et al. Dirac fermions and flat bands in the ideal kagome metal FeSn. Nat. Mater. 19, 163–169 (2020).

    Article  ADS  Google Scholar 

  21. Kenney, E. M., Ortiz, B. R., Wang, C., Wilson, S. D. & Graf, M. J. Absence of local moments in the kagome metal KV3Sb5 as determined by muon spin spectroscopy. J. Phys. Condens. Matter 33, 235801 (2021).

    Article  ADS  Google Scholar 

  22. Yang, S.-Y. et al. Giant, unconventional anomalous Hall effect in the metallic frustrated magnet candidate, KV3Sb5. Sci. Adv. 6, eabb6003 (2020).

    Article  ADS  Google Scholar 

  23. Ortiz, B. R. et al. Superconductivity in the Z2 kagome metal KV3Sb5. Phys. Rev. Mater. 5, 034801 (2021).

    Article  Google Scholar 

  24. Zhao, C. C. et al. Nodal superconductivity and superconducting domes in the topological kagome metal CsV3Sb5. Preprint at https://arxiv.org/abs/2102.08356 (2021).

  25. Ortiz, B. R. et al. Fermi surface mapping and the nature of charge-density-wave order in the kagome superconductor CsV3Sb5. Phys. Rev. X 11, 041030 (2021).

    Google Scholar 

  26. Feng, X., Jiang, K., Wang, Z. & Hu, J. Chiral flux phase in the kagome superconductor AV3Sb5. Sci. Bull. 66, 1384–1388 (2021).

    Article  Google Scholar 

  27. Tan, H., Liu, Y., Wang, Z. & Yan, B. Charge density waves and electronic properties of superconducting kagome metals. Phys. Rev. Lett. 127, 046401 (2021).

    Article  ADS  Google Scholar 

  28. Denner, M. M., Thomale, R. & Neupert, T. Analysis of charge order in the kagome metal AV3Sb5 (A = K, Rb, Cs). Phys. Rev. Lett. 127, 217601 (2021).

    Article  ADS  Google Scholar 

  29. Lin, Y.-P. & Nandkishore, R. M. Complex charge density waves at Van Hove singularity on hexagonal lattices: Haldane-model phase diagram and potential realization in the kagome metals AV3Sb5 (A = K, Rb, Cs). Phys. Rev. B 104, 045122 (2021).

    Article  ADS  Google Scholar 

  30. Park, T., Ye, M. & Balents, L. Electronic instabilities of kagome metals: saddle points and Landau theory. Phys. Rev. B 104, 035142 (2021).

    Article  ADS  Google Scholar 

  31. Zhao, J., Wu, W., Wang, Y. & Yang, S. A. Electronic correlations in the normal state of the kagome superconductor KV3Sb5. Phys. Rev. B 103, L241117 (2021).

    Article  ADS  Google Scholar 

  32. Christensen, M. H., Birol, T., Andersen, B. M. & Fernandes, R. M. Theory of the charge-density wave in AV3Sb5 kagome metals. Preprint at https://arxiv.org/abs/2107.04546 (2021).

  33. Lawler, M. J. et al. Intra-unit-cell electronic nematicity of the high-Tc copper-oxide pseudogap states. Nature 466, 347–351 (2010).

    Article  ADS  Google Scholar 

  34. Ni, S. et al. Anisotropic superconducting properties of kagome metal CsV3Sb5. Chinese Phys. Lett. 38, 057403 (2021).

    Article  ADS  Google Scholar 

  35. Xiang, Y. et al. Twofold symmetry of c-axis resistivity in topological kagome superconductor CsV3Sb5 with in-plane rotating magnetic field. Nat. Commun. 12, 6727 (2021).

    Article  ADS  Google Scholar 

  36. Mesaros, A. et al. Commensurate 4a0-period charge density modulations throughout the Bi2Sr2CaCu2O8+x pseudogap regime. Proc. Natl Acad. Sci. USA 113, 12661–12666 (2016).

    Article  Google Scholar 

  37. Hu, Y. et al. Charge-order-assisted topological surface states and flat bands in the kagome superconductor CsV3Sb5. Preprint at https://arxiv.org/abs/2104.12725 (2021).

  38. Zhao, H. et al. Atomic-scale fragmentation and collapse of antiferromagnetic order in a doped Mott insulator. Nat. Phys. 15, 1267–1272 (2019).

    Article  Google Scholar 

  39. Fauqué, B. et al. Magnetic order in the pseudogap phase of high-Tc superconductors. Phys. Rev. Lett. 96, 197001 (2006).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank A. Soumyanarayanan and J. E. Hoffman for providing the NbSe2 STM data used for analysis in Extended Data Fig. 4. We are also thankful to Rafael Fernandes for insightful conversations. I.Z. gratefully acknowledges support from the National Science Foundation grant NSF-DMR-1654041 and Boston College startup. S.D.W., B.R.O. and T.P. acknowledge support from the University of California Santa Barbara (UCSB) NSF Quantum Foundry funded via the Quantum Materials Science, Engineering and Information (Q-AMASE-i) program under award DMR-1906325. B.R.O. also acknowledges support from the California NanoSystems Institute through the Elings Fellowship program. Z.W. acknowledges support from the US Department of Energy, Basic Energy Sciences, grant no. DE-FG02-99ER45747 and the Cottrell SEED Award no. 27856 from the Research Corporation for Science Advancement. L.B. is supported by the NSF CMMT program under grant no. DMR-2116515. M.Y. is supported in part by the Gordon and Betty Moore Foundation through grant GBMF8690 to UCSB and by the National Science Foundation under grant no. NSF PHY-1748958. T.P. was supported by the National Science Foundation through Enabling Quantum Leap: Convergent Accelerated Discovery Foundries for Q-AMASE-i under award no. DMR-1906325.

Author information

Author notes

  1. These authors contributed equally: Hong Li, He Zhao.

Authors and Affiliations

  1. Department of Physics, Boston College, Chestnut Hill, MA, USA

    Hong Li, He Zhao, Ziqiang Wang & Ilija Zeljkovic

  2. Materials Department, University of California Santa Barbara, Santa Barbara, CA, USA

    Brenden R. Ortiz & Stephen D. Wilson

  3. California Nanosystems Institute, University of California Santa Barbara, Santa Barbara, CA, USA

    Brenden R. Ortiz & Stephen D. Wilson

  4. Department of Physics, University of California Santa Barbara, Santa Barbara, CA, USA

    Takamori Park

  5. Kavli Institute for Theoretical Physics, University of California Santa Barbara, Santa Barbara, CA, USA

    Mengxing Ye & Leon Balents

  6. Canadian Institute for Advanced Research, Toronto, Canada

    Leon Balents

Authors
  1. Hong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. He Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Brenden R. Ortiz
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Takamori Park
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Mengxing Ye
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Leon Balents
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Ziqiang Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Stephen D. Wilson
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Ilija Zeljkovic
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

STM experiments and data analysis were performed by H.L. and H.Z. B.R.O. synthesized and characterized the samples under the supervision of S.D.W. T.P., M.Y., L.B. and Z.W. provided theoretical inputs on the underlying physics and data interpretation. H.L., H.Z., S.D.W., Z.W., L.B. and I.Z. wrote the paper, with input from all the authors. I.Z. supervised the project.

Corresponding author

Correspondence to Ilija Zeljkovic.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Physics thanks Donglai Feng and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data

Extended Data Fig. 1 STM topographs of the K layer.

(a) Large scale STM topograph of 50 nm square region showing the half-K layer (K surface reconstruction where every other K atom is likely cleaved of) as bright regions, and the Sb layer as dark regions. (b) STM topograph zoomed in on a half-K termination with twice the lattice constant of a full K layer (a = 1.1 nm). STM setup condition: (a) Iset = 10 pA, Vsample = 1 V; (b) Iset = 100 pA, Vsample = 20 mV. Data was acquired on sample C with tip 5.

Extended Data Fig. 2 STM imaging of a CDW domain boundary.

(a,b) STM topographs of a region encompassing a CDW domain boundary taken at (a) 20 mV and (b) −10 mV. The white dashed line in (a,b) is a visual guide used to separate the two domains. A more obvious difference between the two domains can be seen in (b). Insets in upper right and lower left corners of (a) represent average dI/dV spectra over the corresponding domains. (c) Fourier transform (FT) of domain (I) and domain (II) in (f). Atomic Bragg peaks and CDW peaks are denoted by black and blue symbols, respectively. (d,e) The FT amplitude dispersions of the 3 CDW peaks extracted from the (d) green and (e) red squares in (b), demonstrating the change in the CDW symmetry axis from \(Q_{2a0}^c\) to \(Q_{2a0}^b\) across the domain wall. (f) Zoomed in image of topographs and dI/dV maps in green (upper row) and red (lower row) squares in (b). (g,h) Fourier-filtered STM topograph including only (g) \(Q_{2a0}^c\) or (h) \(Q_{2a0}^b\) Fourier peaks. STM setup conditions: (a) Iset = 250 pA, Vsample = 20 mV; (b) Iset = 60 pA, Vsample = −10 mV; (d,e) Iset = 400 pA, Vsample = 20 mV, Vexc = 1 mV; (f) Iset = 150 pA, Vsample = −10 mV, Vexc = 1 mV. Data was acquired on sample A using tip 2.

Extended Data Fig. 3 Absence of magnetic field induced CDW reversal and visualizing the temperature evolution of the CDW in KV3Sb5.

(a-c) STM topographs of the Sb termination taken at −3 T, 0 T and 3 T over an identical region with the same tip. (d) Average dI/dV spectra acquired over (a-c), which appear indistinguishable within the resolution of the dataset. (e-g) 2a0 CDW peak amplitude dispersion at the three magnetic fields for (e) \(Q_{2a0}^a\), (f) \(Q_{2a0}^b\), and (g) \(Q_{2a0}^c\). There is almost no difference among data at different fields. (h-j) 2a0 CDW peak amplitude dispersion at 4.5 K, 20 K, and 25 K respectively over the same region of the sample, showing the dominant peak \(Q_{2a0}^b\) getting weaker at higher temperature. (k) A Fourier transform of dI/dV map acquired at 2 mV. The lower left corner of (k) is a zoomed-in high resolution dI/dV map at 2 mV. Atomic Bragg peaks are marked by black dashed circles, while \(Q_{2a0}^a,\) \(Q_{2a0}^b,\) \(Q_{2a0}^c\) are denoted by red square, green circle and blue triangle, respectively. STM setup conditions: (a-c) Iset = 100 pA, Vsample = 50 mV, (d-j) Iset = 100 pA, Vsample = 50 mV, Vexc = 4 mV. Data was acquired on sample D using tip 6.

Extended Data Fig. 4 Isotropic CDW peak dispersion in 2H- NbSe2.

(a) STM topograph of the Se surface of 2H-NbSe2 with the well-known tri-directional 3a0 CDW. (b) The Fourier transform (FT) of (a). Atomic Bragg peaks are circled in black, while the three inequivalent 3a0 CDW peaks are denoted by the blue circle, red square and green triangle. (c) CDW peak amplitude as a function of energy (STM bias) for the three inequivalent directions. Each point is obtained by a two-dimensional Gaussian fit of the CDW peak in the FTs of dI/dV maps. The CDW amplitude profiles along the three directions closely resemble each other, consistent with the expected tri-directional nature of the CDW that does not break rotation symmetry of the lattice. (d) dI/dV maps at −60 mV, 0 mV and 60 mV (from left to right) over the same region shown in (a). (e) FT of 0 mV dI/dV map in (d). Black circles denote the atomic Bragg peaks, while the blue, red and green symbols denote the three inequivalent CDW peaks. STM setup conditions: (a,c,d) Iset = 300 pA, Vsample = −60 mV, Vexc = 3 mV. The data was acquired in the Hoffman lab at Harvard University, and provided for analysis by Anjan Soumyanarayanan and Jenny Hoffman.

Extended Data Fig. 5 Reproducibility of the magnetic field measurements from three different Sb regions of a KV3Sb5 sample.

(a-c) From left to right: STM topographs as a function of magnetic field, Fourier transform (FT) of STM topograph at 0 T, and the amplitude dispersion of different CDW peaks as a function of magnetic field. The three inequivalent 2a0 CDW peaks are enclosed in triangle, circle and square markers, respectively. As it can be seen, the amplitude of different CDW peaks remains nearly identical with the application and the reversal of magnetic field. Magnetic field is applied perpendicular to the sample surface. STM setup conditions: (a) Iset = 400 pA, Vsample = 20 mV; (b) Iset = 150 pA, Vsample = 40 mV; (c) Iset = 150 pA, Vsample = 10 mV; (d) Iset = 100 pA, Vsample = 50mV. Data was acquired on sample A, using (a) tip 4 and (b,c) tip 3.

Extended Data Fig. 6 Magnetic field measurements of cousin compound CsV3Sb5.

(a-c) STM topograph of a 70 nm square Sb surface of CsV3Sb5 in a magnetic field of 4 T, 0 T and −4 T, respectively. Magnetic field is applied perpendicular to the sample surface. (d) The Fourier transform of STM topograph in (b). The unidirectional 4a0 charge ordering peak, 2a0 peaks and atomic Bragg peaks are marked by orange, blue and green markers, respectively. (e) Fourier transform peak amplitudes of different wave vectors. We can observe that none of the charge ordering peak intensities significantly change. (f) The amplitude of the 4a0 CDW peak as a function of bias extracted from a DOS map acquired over the Sb surface of the CsV3Sb5 sample. The 3 different colors in (f) denote data acquired in different magnetic fields. STM setup conditions: (a-c) Iset = 110 pA, Vsample= −40 mV. (f) Iset = 80 pA, Vsample = 20 mV, Vexc = 1 mV.

Extended Data Fig. 7 An example of how a small tip change can strongly influence CDW amplitudes.

(a,b) STM topographs of the Sb termination at (a) −5 T and (b) +5 T magnetic field applied along the c-axis. An obvious tip change occurred while scanning at −5 T. After the image in (a) was acquired, the tip was withdrawn, the magnetic field was changed to +5 T, and then the topograph in (b) over the same region of the sample was taken. We refer to the tip before the tip change as tip 0, and the one after the tip change as tip 1. The green and red squares denote the same areas in the two topographs. Red square (region A) is scanned at different field with the same tip (tip 1), while the green square (region B) is scanned with slightly different tips (tip 0 at −5 T and tip 1 at +5 T). (c,d) The plot of CDW peak amplitudes in Fourier transforms of ±5 T topographs for regions A and B, respectively. From plot (c), the relative amplitude between the 3 CDW peaks is: \(Q_{2a0}^c\) > \(Q_{2a0}^a\) = \(Q_{2a0}^b\) for both +5 T and −5 T. In contrast, the relation between peaks changes dramatically in plot (d), where \(Q_{2a0}^c\) > \(Q_{2a0}^b\) > \(Q_{2a0}^a\) at −5 T and \(Q_{2a0}^c\) > \(Q_{2a0}^a\) > \(Q_{2a0}^b\) at +5 T. From this, it appears as if there is field-dependent CDW rotation. However, this is purely an artifact of a tiny tip change, since it did not happen in the red region above, where two topographs are taken with the same tip. We emphasize that the tip change is tiny and difficult to discern by comparing topographs by eye (we identified it by the abrupt height change denoted by purple arrow in (a)). As such, extreme caution should be taken when interpreting relative amplitudes between different data sets. STM setup conditions: (a,b) Iset = 400 pA, Vsample = 40 mV.

Extended Data Fig. 8 Representative raw data (without drift correction).

(a-e) dI/dV maps of Sb termination without drift correction taken at different bias used in Fig. 2, and (f-j) corresponding Fourier transforms (FTs). (k-o) Raw dI/dV maps that are used in Fig. 3, and (p-t) corresponding FTs without drift correction. STM setup conditions: (a-e) Iset = 600 pA, 400 pA, 200 pA, 200 pA and 400 pA respectively, with Vsample= −300 mV, −200 mV, −100 mV, 100 mV, 200 mV (in the same order); (k-o) Iset = 150 pA, Vsample = 10 mV, Vexc = 1 mV. Data was acquired on sample A using (a-j) tip 2 and (k-t) tip 3.

Extended Data Fig. 9 Additional raw data (without drift correction).

(a-c) Topographs used in Fig. 4, and (d-f) corresponding Fourier transforms without drift-correction. STM setup conditions: (a-c) Iset = 100 pA, Vsample = 50 mV. Data was acquired on sample B using tip 4.

Source data

Source Data Fig. 1

Scatter plot in Fig. 1e.

Source Data Fig. 3

Scatter plots in Fig. 3c,e.

Source Data Fig. 4

Scatter plots in Fig. 4d,e.

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, H., Zhao, H., Ortiz, B.R. et al. Rotation symmetry breaking in the normal state of a kagome superconductor KV3Sb5. Nat. Phys. 18, 265–270 (2022). https://doi.org/10.1038/s41567-021-01479-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/s41567-021-01479-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing