Abstract
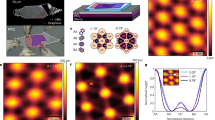
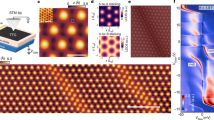
The interplay between strong electron–electron interactions and band topology can produce electronic states that spontaneously break symmetries. The discovery of flat bands in magic-angle twisted bilayer graphene (MATBG)1,2,3 with non-trivial topology4,5,6,7 has provided a compelling platform in which to search for new symmetry-broken phases. Recent scanning tunnelling microscopy8,9 and transport experiments10,11,12,13 have revealed a sequence of topological insulating phases in MATBG near integer filling of the electronic bands produced by the moiré pattern. These correspond to a simple pattern of flavour-symmetry-breaking Chern insulators that fill bands of different flavours one after the other. Here we report the high-resolution local compressibility measurements of MATBG with a scanning single-electron transistor, which reveal an additional sequence of incompressible states with unexpected Chern numbers observed down to zero magnetic field. We find that the Chern numbers for eight of the observed incompressible states are incompatible with the simple picture in which the bands are sequentially filled. We show that the emergence of these unusual incompressible phases can be understood as a consequence of broken translation symmetry that doubles the moiré unit cell and splits each flavour band in two. Our findings expand the known phase diagram of MATBG, and shed light on the origin of the close competition between different correlated phases in the system.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Data availability
Source data are provided with this paper. All other data that support the findings of this paper are available from the corresponding authors upon request.
Code availability
The code that supports the findings of this study is available from the corresponding authors upon reasonable request.
References
Bistritzer, R. & MacDonald, A. H. Moiré bands in twisted double-layer graphene. Proc. Natl Acad. Sci. USA 108, 12233–12237 (2011).
Cao, Y. et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices. Nature 556, 80–84 (2018).
Cao, Y. et al. Unconventional superconductivity in magic-angle graphene superlattices. Nature 556, 43–50 (2018).
Po, H. C., Zou, L., Vishwanath, A. & Senthil, T. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene. Phys. Rev. X 8, 031089 (2018).
Song, Z. et al. All magic angles in twisted bilayer graphene are topological. Phys. Rev. Lett. 123, 036401 (2019).
Ahn, J., Park, S. & Yang, B.-J. Failure of Nielsen-Ninomiya theorem and fragile topology in two-dimensional systems with space-time inversion symmetry: application to twisted bilayer graphene at magic angle. Phys. Rev. X 9, 021013 (2019).
Po, H. C., Zou, L., Senthil, T. & Vishwanath, A. Faithful tight-binding models and fragile topology of magic-angle bilayer graphene. Phys. Rev. B 99, 195455 (2019).
Nuckolls, K. P. et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene. Nature 588, 610–615 (2020).
Choi, Y. et al. Correlation-driven topological phases in magic-angle twisted bilayer graphene. Nature 589, 536–541 (2021).
Wu, S., Zhang, Z., Watanabe, K., Taniguchi, T. & Andrei, E. Y. Chern insulators, Van Hove singularities and topological flat bands in magic-angle twisted bilayer graphene. Nat. Mater. 20, 488–494 (2021).
Saito, Y. et al. Hofstadter subband ferromagnetism and symmetry-broken Chern insulators in twisted bilayer graphene. Nat. Phys. 17, 478–481 (2021).
Das, I. et al. Symmetry-broken Chern insulators and Rashba-like Landau-level crossings in magic-angle bilayer graphene. Nat. Phys. 17, 710–714 (2021).
Park, J. M., Cao, Y., Watanabe, K., Taniguchi, T. & Jarillo-Herrero, P. Flavour Hund’s coupling, Chern gaps and charge diffusivity in moiré graphene. Nature 592, 43–48 (2021).
Yankowitz, M. et al. Tuning superconductivity in twisted bilayer graphene. Science 363, 1059–1064 (2019).
Lu, X. et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene. Nature 574, 653–657 (2019).
Sharpe, A. L. et al. Emergent ferromagnetism near three-quarters filling in twisted bilayer graphene. Science 365, 605–608 (2019).
Serlin, M. et al. Intrinsic quantized anomalous Hall effect in a moiré heterostructure. Science 367, 900–903 (2020).
Stepanov, P. et al. Untying the insulating and superconducting orders in magic-angle graphene. Nature 583, 375–378 (2020).
Xie, Y. et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene. Nature 572, 101–105 (2019).
Kerelsky, A. et al. Maximized electron interactions at the magic angle in twisted bilayer graphene. Nature 572, 95–100 (2019).
Choi, Y. et al. Electronic correlations in twisted bilayer graphene near the magic angle. Nat. Phys. 15, 1174–1180 (2019).
Jiang, Y. et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene. Nature 573, 91–95 (2019).
Liu, J., Liu, J. & Dai, X. Pseudo Landau level representation of twisted bilayer graphene: band topology and implications on the correlated insulating phase. Phys. Rev. B 99, 155415 (2019).
Bultinck, N. et al. Ground state and hidden symmetry of magic-angle graphene at even integer filling. Phys. Rev. X 10, 031034 (2020).
Bultinck, N., Chatterjee, S. & Zaletel, M. P. Mechanism for anomalous Hall ferromagnetism in twisted bilayer graphene. Phys. Rev. Lett. 124, 166601 (2020).
Tomarken, S. L. et al. Electronic compressibility of magic-angle graphene superlattices. Phys. Rev. Lett. 123, 046601 (2019).
Martin, J., Feldman, B. E., Weitz, R. T., Allen, M. T. & Yacoby, A. Local compressibility measurements of correlated states in suspended bilayer graphene. Phys. Rev. Lett. 105, 256806 (2010).
Wong, D. et al. Cascade of electronic transitions in magic-angle twisted bilayer graphene. Nature 582, 198–202 (2020).
Zondiner, U. et al. Cascade of phase transitions and Dirac revivals in magic-angle graphene. Nature 582, 203–208 (2020).
Streda, P. Theory of quantised Hall conductivity in two dimensions. J. Phys. C 15, L717–L721 (1982).
Xie, M. & MacDonald, A. H. Nature of the correlated insulator states in twisted bilayer graphene. Phys. Rev. Lett. 124, 097601 (2020).
Liu, J., Ma, Z., Gao, J. & Dai, X. Quantum valley Hall effect, orbital magnetism, and anomalous Hall effect in twisted multilayer graphene systems. Phys. Rev. X 9, 031021 (2019).
Guinea, F. & Walet, N. R. Electrostatic effects, band distortions, and superconductivity in twisted graphene bilayers. Proc. Natl Acad. Sci. USA 115, 13174–13179 (2018).
Kang, J. & Vafek, O. Non-Abelian Dirac node braiding and near-degeneracy of correlated phases at odd integer filling in magic-angle twisted bilayer graphene. Phys. Rev. B 102, 035161 (2020).
Chen, B.-B. et al. Realization of topological Mott insulator in a twisted bilayer graphene lattice model. Preprint at https://arxiv.org/abs/2011.07602 (2020).
Xie, F. et al. Twisted bilayer graphene. VI. An exact diagonalization study at nonzero integer filling. Phys. Rev. B 103, 205416 (2021).
Regan, E. C. et al. Mott and generalized Wigner crystal states in WSe2/WS2 moiré superlattices. Nature 579, 359–363 (2020).
Xu, Y. et al. Correlated insulating states at fractional fillings of moiré superlattices. Nature 587, 214–218 (2020).
Cao, Y. et al. Superlattice-induced insulating states and valley-protected orbits in twisted bilayer graphene. Phys. Rev. Lett. 117, 116804 (2016).
Kim, K. et al. van der Waals heterostructures with high accuracy rotational alignment. Nano Lett. 16, 1989–1995 (2016).
Efros, A. L. Coulomb gap in disordered systems. J. Phys. C 9, 2021–2030 (1976).
Liu, X. et al. Tuning electron correlation in magic-angle twisted bilayer graphene using Coulomb screening. Science 371, 1261–1265 (2021).
Zhang, Y.-H., Po, H. C. & Senthil, T. Landau level degeneracy in twisted bilayer graphene: role of symmetry breaking. Phys. Rev. B 100, 125104 (2019).
Lian, B. et al. Twisted bilayer graphene. IV. Exact insulator ground states and phase diagram. Phys. Rev. B 103, 205414 (2021).
Acknowledgements
We acknowledge discussions with A. Hamo and B. Lian. This work was primarily supported by the US Department of Energy, Basic Energy Sciences Office, Division of Materials Sciences and Engineering, under award no. DE-SC0001819, and the Gordon and Betty Moore Foundation through grant GBMF9468 to A.Y. Fabrication of samples was supported by the US Department of Energy, Basic Energy Sciences Office, Division of Materials Sciences and Engineering, under award no. DE-SC0019300. Assistance with the transport measurements and data analysis were provided by the National Science Foundation (DMR-1809802) and the STC Center for Integrated Quantum Materials (NSF grant no. DMR-1231319) (Y.C.). P.J.-H. acknowledges support from the Gordon and Betty Moore Foundation’s EPiQS Initiative through grant no. GBMF9463. A.T.P. acknowledges support from the Department of Defense through the National Defense Science and Engineering Graduate Fellowship (NDSEG) Program. Y.X. and S.C. acknowledge partial support from the Harvard Quantum Initiative in Science and Engineering. A.T.P., Y.X. and A.Y. acknowledge support from the Harvard Quantum Initiative Seed Fund. A.V. was supported by a Simons Investigator award and by the Simons Collaboration on Ultra-Quantum Matter, which is a grant from the Simons Foundation (651440). E.K. was supported by a Simons Investigator Fellowship, by NSF-DMR 1411343, and by the German National Academy of Sciences Leopoldina through grant no. LPDS 2018-02 Leopoldina fellowship. P.R.F. acknowledges support from the National Science Foundation Graduate Research Fellowship under grant no. DGE 1745303. This research is funded in part by the Gordon and Betty Moore Foundation’s EPiQS Initiative, grant no. GBMF8683, to D.E.P. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, via grant no. JPMXP0112101001; JSPS KAKENHI grant no. JP20H00354; and CREST (JPMJCR15F3), JST. This work was performed, in part, at the Center for Nanoscale Systems (CNS), a member of the National Nanotechnology Infrastructure Network, which is supported by the NSF under award no. ECS-0335765. CNS is part of Harvard University.
Author information
Authors and Affiliations
Contributions
A.T.P., Y.X., J.M.P., P.J.-H. and A.Y. designed the experiment. A.T.P. and Y.X. performed the scanning SET experiment and temperature-dependent transport measurements, and analysed the data with input from A.Y. S.H.L., A.T.P. and Y.X. performed the transport measurements in the dilution refrigerator. J.M.P., Y.C. and P.J.-H. designed and provided the samples and contributed to the analysis of the results. J.M.P. and Y.X. carried out the simulation of compressibility. E.K., D.E.P. and A.V. performed the theoretical analysis. K.W. and T.T. provided the hBN crystals. All the authors participated in discussions and in writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Physics thanks Allan MacDonald and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data
Extended Data Fig. 1 Temperature dependent longitudinal resistance.
a, Rxx as a function of carrier density n and temperature from 0.53 K to 11 K. b, Semi-log plot of conductance σxx as a function of inverse temperature at carrier densities indicated by the colored triangles in a. The straight lines are fits to \(\sigma _{xx} \propto {{{\mathrm{exp}}}}( - \frac{{2{{{\mathrm{{\Delta}}}}}}}{{k_BT}})\) for temperature activated behavior. c, Rxx as a function temperature at n = −1.97 × 1012 cm−2 showing a superconducting-like transition.
Extended Data Fig. 2 Evidence for alignment between hBN and MATBG.
a, Optical image of the stack before etching. The arrows labeled ‘hBN’ and ‘G’ indicate the crystallographic edges of the bottom graphene and the bottom hBN, which are aligned with a 60° angular offset. b, Inverse compressibility measurements beyond 𝜈=±4, showing a series of incompressible states. c, Wannier diagram depicting the incompressible states in b. Black and orange lines correspond to states arising from the superlattices formed by MATBG and by the possible alignment between hBN and graphene.
Extended Data Fig. 3 Transport Landau fan diagram of MATBG.
a, Rxx as a function of ν and B at 10 mK. b, Schematic of the Landau level (black) and Chern insulators with even parity (blue) observed in a.
Extended Data Fig. 4 Spatially-resolved compressibility measurements at B = 0 T.
a, Optical image of the MATBG device. X and Y define the coordinate axis. b, Inverse compressibility measurements as a function of carrier density and distance along X at selected Y positions within the white rectangle outlined in a, showing the ubiquity of the incompressible states at ν = 0, 1, 2, 3. c, Local twist angle between the two graphene sheets measured over the region defined by the white rectangle outlined in a. d-g, Local magnitude of thermodynamic gaps at ν = 0, 1, 2, 3 over the region defined by the white rectangle outlined in a, showing correlation between the gaps at ν = 1, 2, 3 and the twist angle.
Extended Data Fig. 5 Mean-field simulation of inverse compressibility.
a, Simplified symmetric triangular density of states (DOS) of the flat bands in MATBG used for the mean-field calculations in b, c and d. b-d, Local inverse compressibility dµ/dn calculated using a mean-field model (see Methods) for J = 0 and U/W = 0.5 (a), 0.8 (b), and 1.1 (c), corresponding to three distinct regimes as shown in e. e, Schematic illustration of the evolution of the gap at integer fillings as a function of Utot/W (here Utot = U + 2 J), showing three distinct regimes separated by two critical values α and β. f, Local inverse compressibility dµ/dn calculated using the DOS shown in the inset with U = 0.55, J = 0.35. The bandwidths of the upper and lower flat bands are 1 and 1.65 and the two bands are separated by an asymmetric sublattice gap ΔAB = 0.35. Our calculation captures the salient features of the measured inverse compressibility in our experiment (Fig. 1e), including the negative compressibility between positive integer fillings. g, Chemical potential µ relative to its value at the CNP as a function of filling factor 𝜈, calculated using the same DOS in the inset to f, with different value of interaction strength and sublattice gap. The parameters used for each case are U = 0.55, J = 0.35, ΔAB = 0.35 for the orange curve, U = 0.55, J = 0.35, ΔAB = 0 for the blue curve, and U = 0.8, J = 0, ΔAB = 0 for the yellow curve. We find that interactions are key to the emergence of the gaps at integer fillings, and the presence of a gap at the CNP enhances the values of the gaps if the interaction is strong enough.
Extended Data Fig. 6 Inverse compressibility and chemical potential at 7.3 T.
a, dµ/dn as a function of moiré band filling factor ν, showing that the incompressible peaks associated with Chern insulators (orange dotted lines) are substantially larger than those of Landau levels (grey dotted lines). b, Chemical potential μ relative to its value at the CNP as a function of moiré band filling factor ν, showing that the energy gaps associated with Chern insulators (orange shaded regions) are substantially larger than those of Landau levels (grey shaded regions).
Extended Data Fig. 7 Spatial dependence of the incompressible states.
Inverse compressibility measurements for electron doping at B = 11.5 T over 0.6 μm along the X and Y directions (see white dotted rectangle in Extended Data Fig. 4a). The states are labeled by ordered pairs (C, s), which denote the associated Chern number C and the moiré band filling s.
Extended Data Fig. 8 Chern numbers of translation-symmetric and translation symmetry breaking incompressible states.
Band filling sequence within the unit cell-doubling model that produces all the experimentally-observed Chern insulators.
Extended Data Fig. 9 Hartree-Fock energetics.
a-c, Different contributions to the energy difference between TS-broken and TS-symmetric states as a function of w0/w1 at ν = +1 (a), +2 (b), +3 (c). While the Fock and the kinetic energy remain nearly unchanged, the Hartree energy increases with 𝜈, in accordance with the expectation of νVH (see Methods). d, The total energy difference as a function of w0/w1 for 𝜈 =+1 (purple), +2 (green), +3 (burgundy), showing that the TS-breaking states and TS-symmetric states are separated by less than 2 meV and TS-breaking states become more competitive when w0/w1 is large.
Extended Data Fig. 10 Thermodynamic gaps at full fillings.
a, b, Chemical potential relative to the CNP near ν = −4 (a) and +4 (b), showing the magnitude of the energy gaps separating the flat bands and the remote bands.
Supplementary information
Supplementary Information
Supplementary Discussions I and II.
Source data
Source Data Fig. 1
Source data for Fig. 1c–f.
Source Data Fig. 2
Source data for Fig. 2a.
Source Data Fig. 3
Source data for Fig. 3b–d.
Source Data Fig. 4
Source data for Fig. 4a,b.
Rights and permissions
About this article
Cite this article
Pierce, A.T., Xie, Y., Park, J.M. et al. Unconventional sequence of correlated Chern insulators in magic-angle twisted bilayer graphene. Nat. Phys. 17, 1210–1215 (2021). https://doi.org/10.1038/s41567-021-01347-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/s41567-021-01347-4
This article is cited by
-
Mapping charge excitations in generalized Wigner crystals
Nature Nanotechnology (2024)
-
Spin skyrmion gaps as signatures of strong-coupling insulators in magic-angle twisted bilayer graphene
Nature Communications (2023)
-
Superconductivity and correlated phases in non-twisted bilayer and trilayer graphene
Nature Reviews Physics (2023)
-
A highly correlated topological bubble phase of composite fermions
Nature Physics (2023)
-
Dirac spectroscopy of strongly correlated phases in twisted trilayer graphene
Nature Materials (2023)